The Spin Consideration
It is always told that the graviton has spin +2 or -2 and that the Higgs particle has spin 0.
Let's propose the vacuum that is gravity to consists of a superposition of a glue2ball field gl  gl
gl  (spin +2) and a glue2ball field gl
(spin +2) and a glue2ball field gl  gl
gl  (spin -2). *)
(spin -2). *)
*) Here gl
means gluon
and a glue2ball is a glueball made of 2 gluons;  = spin +1 and
= spin +1 and  = spin -1.
= spin -1.
The vacuum is built from vacuum marbles placed neatly next to each other in all directions and each marble is called a graviton
. Here this graviton consists of 2 gluons, the vacuum that is gravitation is taken to consist of gravitons made of two gluons each. This is meant to hold only for the third generation, quarks t and b, the tau particle and the tau neutrinos. The reason for this will be made clear in the next two pages. For the moment you can take in mind that the 1rst and 2nd generation are made of likewise composites.
The vacuum that is the 3rd Higgs field **) consists likewise of a glue2ball field gl  gl
gl  and a glue2ball field gl
and a glue2ball field gl  gl
gl  (both spin 0). The vacuum that is the 3rd Higgs field Higgs field is taken to consist of
(both spin 0). The vacuum that is the 3rd Higgs field Higgs field is taken to consist of Higgs particles
, also made of two gluons.
**) With the expression 3rd Higgs field
I again get ahead of the next two pages. Keep in mind for the moment that the 3rd Higgs field belongs to the 3rd generation. If you meet somewhere in this website the expression hadronic Higgs field
or leptonic Higgs field
, that is a previous attempt, by me forgotten so far to be replaced by the expression 3rd Higgs field
.
Suppose one of the two gluons from the graviton gl  gl
gl  absorbs a graviton gl
absorbs a graviton gl  gl
gl  . Three gluons merge easier than two gluons, as is argued at page 7 of the QCD storyline. I tried to work out the gluNon concept at that page. You can read that later if you take for granted that 3 gluons merge easier than 2 gluons. And that 2 gluons can form a glu2on, a composite made of 2 gluons that merge at least not immediately. When the glu2on is colorless I call it a glue2ball.
. Three gluons merge easier than two gluons, as is argued at page 7 of the QCD storyline. I tried to work out the gluNon concept at that page. You can read that later if you take for granted that 3 gluons merge easier than 2 gluons. And that 2 gluons can form a glu2on, a composite made of 2 gluons that merge at least not immediately. When the glu2on is colorless I call it a glue2ball.
( gl  , spin +1) + ( gl
, spin +1) + ( gl  gl
gl  , spin -2) --> ( gl
, spin -2) --> ( gl  , spin -1) (1.1)
, spin -1) (1.1)
Here ( gl  , spin +1) is one of the two gluons from gl
, spin +1) is one of the two gluons from gl  gl
gl  . The other gluon from the pair gl
. The other gluon from the pair gl  gl
gl  remains unaffected. The disappeared graviton leaves an empty spot at the place it had occupied. So the two gravitons change into one empty spot and one Higgs particle of same volume (is assumed) as the graviton:
remains unaffected. The disappeared graviton leaves an empty spot at the place it had occupied. So the two gravitons change into one empty spot and one Higgs particle of same volume (is assumed) as the graviton:
gl  gl
gl  + gl
+ gl  gl
gl  --> gl
--> gl  gl
gl  + empty spot (1.2)
+ empty spot (1.2)
Then the Higgs particle gl  gl
gl  is absorbed at the coupling of some particle in the course of renormalization, leaving another empty place there.
is absorbed at the coupling of some particle in the course of renormalization, leaving another empty place there.
So finally 2 gravitons converted to 2 empty spots and 1 Higgs absorption. (1.3)
This process rules out the possibility of taking e.g. the gl  gl
gl  as vacuum particle while the other, gl
as vacuum particle while the other, gl  gl
gl  , could be real. We need them both as vacuum particles.
, could be real. We need them both as vacuum particles.
If one gluon in graviton gl  gl
gl  and one gluon in graviton gl
and one gluon in graviton gl  gl
gl  would just interchange their spin, one gets gl
would just interchange their spin, one gets gl  gl
gl  and gl
and gl  gl
gl  , which are two Higgs particles. Now there are two Higgs particles created in one single strike to be absorbed in the course of renormalization. This is thought to take place at the location of a quark, the quark mediates this spin conversion.
, which are two Higgs particles. Now there are two Higgs particles created in one single strike to be absorbed in the course of renormalization. This is thought to take place at the location of a quark, the quark mediates this spin conversion.
So then 2 gravitons convert to 2 empty spots and 2 Higgs absorptions. (1.4)
(1.4) might yield a heavier particle than (1.3) and might only form when sufficient amounts of energy are available. The Higgs mechanism (1.4) should work then all over the track of the heavy particle as long as sufficient energy is available.
The sagging in of the vacuum field into the two empty spots yields two units
of gravitation. The one or two Higgs absorption embody one or two units
of acquiring mass. For the ponderable mass (causing the gravitational field) to be proportional to the inert mass, which is the main assuption in GR (general relativity), the amount of empty spots must be proportional to the number of Higgs absorptions.
In (1.1) and (1.2) graviton 1, to give them names, had absorbed vacuum marble graviton 2 and in doing so acquires the energy of graviton 2 added to its own energy. It is not precisely the Higgs mechanism because it had absorbed a graviton and not a Higgs particle. So it is in doubt whether the absorbing graviton gains mass. But it has caused one empty spot that will be filled in from the outside and this is one bit of gravitation. A vacuum locally acquiring energy, a local excited state of the vacuum, is not yet defined, maybe even not possible. So we conclude this reaction will not take place spontaneously in empty space. But it does occur in the neighborhood of a quark ready to give that quark its mass. (1.5)
So we conclude there don't have to be two fields, a gravitational field AND a Higgs field. When a Higgs vacuum marble emerges, it is absorbed immediately thereafter. The 3rd generation vacuum then is one single grid of gravitons. The 3rd Higgs field, its Higgs particle, only does exist as a short-living intermediate state between the gravitational field and any coupling anywhere. The link between space and matter. (1.6)
The gravitational field consists of what we called gravitons, marble-like pieces of space. Sometimes the gravitons are filled in with colored gluon pairs, in doing so forming the third Higgs field. The field consisting of colored gluon pairs is the strongest field and it is this field that is supposed to form the vacuum, the grid onto which all events are attached. More about it below.
Superposed to the colored gluon pairs Higgs field for the 1rst generation are the spin 0 photon Higgs field for the 2nd generation and the spin 0 neutrinophoton Higgs field for the 1rst generation. More about it in the next two pages.
Mind superposed contributions don't see each other. An absorption from a Higgs field choses which Higgs field becomes real, at that spacetime point of absorption. The absorption holds as a measurement of the Higgs field.
As said, the 1rst generation (quarks u and d, the electron and the positron, and the electron neutrinos) absorps from the neutrinophoton Higgs field. The absorption from the Higgs field is the only connection with the vacuum, the only way to conclude that the absorbing particle is here and now. As long as the absorbing particle does so, there is no connection to the third Higgs field, the vacuum made of colored gluon pairs. So as far as our interactions reach, the third field doesn't exist, although it still is the strongest vacuum field. We, ordinary people, absorb from the 1rst Higgs field, the neutrinophoton vacuum field, and that is the field with respect to which are defined our measurements of space (in meters) and time (in seconds).
The u and d quark from the first generation react with colorforce at a pace of 10^23 reactions per second. To give the u and d quark its mass in every reaction, I am forced to conclude that the neutrinophoton absorption must have this pace too. In the next two pages will appear reasons how this comes to be.
As observed from us, the three Higgs fields are superposed onto each other. But what are the three field doing when we are not looking? That is, when there is no absorption from one of the fields? In between the absorptions, as to speak? Do the three Higgs field cohere to one vacuum field, when we are not looking? Is spacetime spanned up by the third Higgs field, the colored gluon pairs field? Then somehow the neutrinophoton Higgs field is an actor, just an actor, in the play of the spacetime gluon pair Higgs field.
Take (3.1), (3.2) and (3.3). We take ( i -i ) as a vacuum particle, a vacuum marble, consisting of the gluons i and -i, where i and -i are quaternion units.
We start with two neighboring vacuum marbles, e.g.
( i -i ) ( i -i ) (2.1)
This is not a multiplication, it are just two neighboring vacuum particles placed next to each other. Now we assume the right gluon of the first vacuum marble ( -i ) to absorb the entire second vacuum marble ( i -i ). Therefore we have to multiply all merging gluon colors (now given by quaternion units). The left gluon of that first vacuum marble is unaffected.
If we rename ( i -i ) ( i -i ) as ( i a ) ( b c ) then there are 6 multiplication orders: abc, acb, bac, bca, cab, cba. In gluon-gluon reactions there is no preferred multiplication order and so the 6 possible outcomes superpose. In this case they all give same outcome -i, so the superposed possibilities merge to one possibility again.
-i * i * -i = -i * -i * i = i * -i * -i = i * -i * -i = -i * i * -i = -i * -i * i = -i (2.2)
The result is, as far as the colors are concerned, that the first vacuum marble is unchanged and the second vacuum marble is absorbed, leaving behind a hole in the vacuum, in accordance with the spin consideration.
(Quaternion multiplication has the associative property. As long as you don't change the order of multiplication, it doesn't matter whether you first multiply the last two gluons and then multiply by the first gluon, or multiply the first and second gluon and then multiply with the third one.)
The vacuum now is a superposition of ( i -i ), ( j -j ), ( k -k ) and ( 1 1 ) from (2.8) at the previous page, each in spin state gl  gl
gl  or gl
or gl  gl
gl  . So 8 fields altogether. (2.3)
. So 8 fields altogether. (2.3)
Let's pick up (3.2) again. We have a Higgs particle gl  gl
gl  . The conversion in which the Higgs particle was created, is thought to take place at the location of a quark, the quark mediates this spin conversion. Take in mind a baryon, three quarks together. If this conversion also detaches the gluons from each other, then you have two independent gluons of opposite color. Then one gluon can go to the second quark and the other to the third quark.
. The conversion in which the Higgs particle was created, is thought to take place at the location of a quark, the quark mediates this spin conversion. Take in mind a baryon, three quarks together. If this conversion also detaches the gluons from each other, then you have two independent gluons of opposite color. Then one gluon can go to the second quark and the other to the third quark.
(gl  gl
gl  ) Higgs particle --> (gl
) Higgs particle --> (gl  ) (gl
) (gl  ) two independent gluons (2.4)
) two independent gluons (2.4)
So 2 gravitons disappear from the vacuum, reducing it by their volume, and 2 gluons appear. Vacuum converts into matter. Subsequently the gluons are absorbed by the two quarks which is the Higgs field absorbing giving them mass. (2.5)
table (2.6)
Graviton 1 is the same in all 5 columns. Graviton 2 is in all its possible compositions.
In the Feynman-diagram of the baryon it must be something like the following (quaternion parts only). You have a baryon with start state u-quark of color i, d-quark of color j and a third quark of color k (k-quark not shown). Then a vacuum particle ( -k k ) appears.
i * j
i * 1 * j
1 is the value of the vacuum particle ( -k k )
= i * -k * k * j
The vacuum particle appears
= i * -k * j * -k
The colors of the vacuum particle have detached from each other. Then quark i absorbs gluon -k and quark j absorbs the other gluon -k. Mark when it would have been quark i that EMITS a gluon -k and quark j that ABSORBS the gluon -k, then the equations are precisely the same. See page 2 of QQD.
= j * -i (2.7)
or likewise leading to end state
= i * k * j * k
= -j * i (2.8)
As you see, just like in accepted QCD the u-quark and the d-quark have swapped color: the u-quark now has color j and the d-quark has color i. Only a minus sign appeared in front of one of the colors of the quarks that swapped color.
Mathematically this minus sign is not a surprise. A quaternion rule is that when you swap two different quaternion units, like i and j, then there appears a minus sign in front:
i * j = - ( j * i ) = -j * i = j * -i
But what is the physical meaning of this, what to do with the minus sign? In paragraph Mesons at page 3 of QQD this minus sign doesn't appear in the same reasoning for mesons. (2.9)
The paragraph Minus Sign Go Wild
, below the black bar, has been very seductive, but there is chosen to regard it as a Previous Attempt and is abandoned.
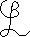
Nowadays insights reveal that the Higgs mechanism described so far is the Higgs mechanism for the 3rd generation: the quarks b and t, the tauon and the tau-neutrinos. The 1rst and 2nd generation have a different Higgs mechanism, see the next two pages of this storyline. The Higgs mechanism of the gluon pair field might be used not too often in our daily life, but the vacuum grid of the gluon pair field is still important for all generations. As the strongest and the fastest reacting field the colored gluon pair vacuum field is regarded as the grid to which all events are attached, the background grid relative to which all renormalizations are performed.
Let's regard some more properties of this 3rd generation Higgs mechanism.
When the electron absorbs from the Higgs field, it gains mass. But here there are two particles, quark i and quark j, that absorb from the Higgs field. So we assume both particles to gain mass.
What happened was that 2 gravitons as we call the vacuum particles, convert into 1 Higgs particle nearby a quark, the Higgs particle converts to 2 separate gluons that are absorbed by two neighboring quarks, see table (2.6) and that is the Higgs mechanism.
This might be all there is to the exchange of gluons in the baryon. It is possible that there are no gluons going from one quark to another one, and that there only is absorption from the Higgs field. The result is the same: a swap of colors. It might be a quark never emits a gluon, they only absorb gluons, in pairs made on the spot. For every gluon pair that is absorbed, there disappears the volume of one graviton from the vacuum.
(Originally in the QCD storyline, page 2, is stated: It is as if the gluon takes away the color of the emitting quark in its upper half AND THEN A COLOR-ANTICOLOR-PAIR OF ITS DESTINATION APPEARS, a so-called correlated pair of particles, a correlated pair of colors cyan-red
. So in the definition of the gluon reaction itself in QCD the emergence of a kind of vacuum particle has been there from the start.)
Maybe the processes superpose? Direct gluon exchange superposes with Higgs field absorption? Decisive might be an energy consideration. If you have the choice OR to provide the energy for an intermediating gluon, albeit only for a short time, OR you can get it for free from the vacuum, just being there to be absorbed, then the choice seems to be easy. The lowest energy one will be chosen most often, if not always.
Unless energy is available and the higher-energy possibility is faster.
So I guess the possibilities do superpose, but the gluon-interchange reaction from accepted QCD will contribute little or nothing. (2.10)
In accepted QCD direct gluon exchange is the very mechanism by which quarks attract each other. So we conclude
The Higgs mechanism for the 3rd generation not only provides mass but might also form (the main part of) the attraction between the quarks of the 3rd generation. (2.11)
For the gluonic Higgs mechanism to work, it needs TWO particles. Sole quarks cannot be given mass by the gluonic Higgs mechanism.
IF YOU ARE READING TONE FOR THE FIRST TIME, ALL NECESSARY THINGS FOR THE CHAPTERS TO COME ARE GIVEN NOW, YOU CAN SKIP THE REST OF THE PAGE AND READ IT LATER.
Minus Sign Go Wild is extraordinary. However, it is now considered to be a previous attempt.
Let's return to the question What to do with the minus sign?
from (2.9).
Once again I can feel the temptation to go wild
about the minus-signs, take the minus sign as a real property and in (2.7) regard the new color -i as cyan  , a d-quark with anticolor -i. Let's just take the 3 quarks in the baryon to have color i, j and k and whatever plus or minus signs are in front of them, their multiplication always will yield the colorless +1 or -1 end state, that thus is permitted. So let's go on with the baryon with colors j -i k, or in (2.8) with -j i k. This way of treating colors is what is called
, a d-quark with anticolor -i. Let's just take the 3 quarks in the baryon to have color i, j and k and whatever plus or minus signs are in front of them, their multiplication always will yield the colorless +1 or -1 end state, that thus is permitted. So let's go on with the baryon with colors j -i k, or in (2.8) with -j i k. This way of treating colors is what is called minus sign go wild
.
Consider table (2.6), the outcome of column 2, ( k ) ( k ) + ( -k ) ( -k ). Two gluons appeared, where do they go? We start with a baryon with colors i, j and k, to denote as baryon ( i j k ). When ( k ) ( k ) emerge at the quark with color k then one ( k ) arrives at the quark of color i and the other ( k ) at the quark with color j. Then ik = -j and jk = i, mark we had to right-multiply the quark by the gluon, see (1.3) at page 2 of QQD. The quarks in the baryon then have colors -j, i and k. Now -j * i * k = -1, so this is a permitted end state (being colorless). When i and k would exchange a black glueball then ( -j i k ) converts to ( -j -i -k ) which are the colors of an antibaryon. Three quarks with three anticolors. Application 4 at page 7 of storyline QQD, argues baryons usually might be in a quark-antiquark mix of net color white.
So, as far as the colors are concerned, this reaction converts a baryon into an antibaryon. While the subsequent reaction will turn the antibaryon back into a baryon. Note this alternation doesn't affect the electric charge of the baryon, nor its taste, spin or mass. It's only a color-thing and colors, unlike the four other properties, cannot be observed.
The possibilities for a second set of separated vacuum particles ( k ) ( k ) or ( -k ) ( -k ) next to arrive at baryon ( -j i k ) are:
Table (3.1)
In each of the sets A up to F the first column ( i -j k ) is the baryon - there is no specific order of i, -j and k in the baryon. The second column is (k) and (k), or (-k) and (-k), the gluons that react with the baryon.
A and B are baryons again. In A: when the end states -j and -i would interchange a black glueball (compare Application 4 at page 7 of QQD, nr 1, 2 and 3 in the picture), they would convert to j and i, resulting in baryon ( i j k ). So ( -i -j k ) holds as a baryon state.
In A up to F there is absorbed 1 vacuum particle (Higgs mechanism), the vacuum is reduced by the volume of 1 vacuum particle (gravity).
(Black glueball exchange can also be mimicked by the absorption of a ( -1 -1 ) vacuum particle, that yields the same effect. Alas, according to (2.8) from the previous page the ( -1 -1 ) is no part of our forward time evolving vacuum.)
In C the ( k ) ( k ) gluon pair is assumed to emerge at the quark of color i. The gluons then go to quark -j and k respectively. This results in a meson-like composition ( i -i ) and a quark of color -1. We know white gluons, but what is a black quark? A black quark is a quark that doesn't glue but do couple. Because of the minus sign it would convert the particle it couples to into an antiparticle, or the other way around.
The absorption of the ( k ) ( k ) is the Higgs mechanism, so both the -i (formerly -j) and the -1 (formerly k) acquire mass.
Suppose the baryon is a proton and the i and -i (formerly i and -j) are an u- and d-quark. *) Then our -1 must be an u-quark of spin +1/2 or -1/2. There are two possibilities: it escapes or it doesn't. When it doesn't, the color -1 quark maintains its spin 1/2, taste u and electric charge +2/3, no reason to assume otherwise. Because -1 doesn't glue, the -1 quark is no longer bound by color, only by electric charge. So I expect it to enlarge its distance and form a halo around the ( i -i ) meson-like particle, a zero-color quark-cloud around the remaining two quarks, like the electron does around the nucleus. Well, I guess it would work a lot better when the i and -i were both u and the d circles around them. Both u's have +2/3 electric charge and the d has -1/3 electric charge. So let's do it that way.
*) -i is an anticolor so the quark with this color would be an antiquark, with antitaste anti-u or anti-d then. But let's not bother about not-immediately-fitting properties of the particles within the baryon as long as there is no measurement involved there.
That circling around of d can in principle cause detectability. If whatever particle while passing this baryon structure reacts on the circling property, this holds within the system as a measurement. A particle of -1/3 electric charge as the d is, is never observed, only integer charges are. Massless electric charge has never been observed. So the electric charge must somehow have been redistributed. But how? We only have net one unit of positive electric charge to redistribute. The easiest way is to assume d had transferred its electric charge to one of the two u's, -1/3 + 2/3 = +1/3, leading to the meson of charge +1/3 +2/3 = +1 electric charge. The color -1 d-quark then has no electric charge, there is no electric force keeping it in orbit and it would escape. Another way of electric charge redistribution is that d gets the one positive electric charge, while the u's will have no net electric charge. This d
then is a particle with spin +1/2 or -1/2, one positive electric charge, and color -1. Except for the -1 color it resembles the positron. In the next page the positron is determined to have color +1. Our d could become a positron when the -1 color is dragged away by an electron neutrino that subsequently reaches our u that was left with +1/3 electric charge. The -1 color would convert the u into an anti-u, or u. Somehow this u must be d now, the electric charge fits in with that now. The difference between quark u and d is the electric charge only, isn't it? Anyway, in both cases there is no electric force keeping the d in orbit. Still having color -1 it will escape. The structure cannot exist as a measureable thing.
The d still circling around, just before electric charge redistribution. When distance from d to the two u quarks starts to increase, it becomes increasingly difficult to provide the black d quark with mass by the Higgs mechanism as described so far. Two separate gluons (former vacuum particle) have to go to two quarks but when one of them is at larger distance the gluon that has to reach for it, has to travel too long a distance. The black d quark has color value -1 and is not attracted by the two u quarks by color force. We concluded in (2.11) that attraction between quarks IS the Higgs mechanism. So the Higgs mechanism doesn't work between the black d quark and the two u quarks. So the black d quark is massless. It gains lightspeed and so will not be kept in orbit. It escapes after the short transition time. Since massless electric charges has never been observed, an electric charge redistribution as described in the previous paragraph must have taken place before the massless takeoff of the former d.
Could the escaping -1 be a black glueball? The black glueball is massive according to (2.7) and further at the previous page. Our quarks have spin 1/2, the black glueball as well as the meson have integer spin. So it seems no, it cannot be the black glueball. Unless there is an extra particle conveying the missing +1/2 or -1/2 spin - the neutrino does such a thing.
Table (3.1)
In D results meson ( i i ) and a white quark, massive because of Higgs absorption. It is massive only at the first instant of its moment of creation. After that moment it is massless. Sole quarks cannot be given mass. Like in C, the white quark becomes a halo, a white-quark cloud around the meson ( i i ) and then it escapes (needs charge redistribution). The meson has value i * i = -1, permitted according to paragraph mesons at page 3 of QQD.
States that transform into each other by internal gluon exchange, superpose. The states before and after gluon exchange are different, they superpose until a measurement is made that uses the difference. Two possibilities are remarkable:
1. When one of the i-quarks interchanges a black glueball with the white quark, then the meson becomes ( i -i ) and the white quark becomes a black quark, precisely as in C.
2. When one of the quarks of color i interchanges a gluon -i with the other quark of color i, then both i's become 1. (I still use the term gluon exchange
but (2.11) indicate the Higgs mechanism prevails over gluon exchange. The results are the same so when we talk about gluon exchange we mean the Higgs mechanism as described.)
We have three 1's now, three colorless quarks, the baryon is ready to decay completely. But the quarks still have electric charges +2/3, +2/3 and -1/3, these have to be redistributed first. The easiest way seems to be that one of the color 1 particles gets +1 electric charge and the other two become electrically neutral. No color force no more between the remaining particles, no electric force either. The baryon decays in its 3 former quarks. Three particles without color, two massless, one with +1 electric charge and thus mass, all have spin 1/2. Do I recognize this? What particles can it be?
E: Resulting are a meson ( -j -j ) and a black quark. Convertible by black glueball exchange to meson ( j -j ) and a white quark, like in F.
F results in meson ( j -j ) and a white quark.
We forgot so far to treat nr 3, 4 and 5 of scheme (2.6). Number 3 is analogous to number 2. Number 4 and 5 are a vacuum particle that has split in ( i ) and ( -i ).
The description so far shows that the existence of baryons (3-quark systems) leads to the existence of mesons (2-quark systems). The mesons of this page are always accompanied by a color +1 or -1 particle. It does not show why the meson is unstable, nor the existence of other generations. Higher generation baryons all decay into another baryon and a meson.
For a pair of gluons to remain massless, the signs in front of the gluons have to be opposite. One gluon has to be a particle (i, j, k or 1) while the other gluon is an antiparticle (-i, -j, -k or -1). The colors don't have to be equal, only the sign in front has to be opposite.
The Mesons paragraph at page 3 of QQD tries to show that the restriction quarks have color and antiquarks have anticolor
is compulsory. This restriction or something the like, I am not completely sure about that. And when it holds for mesons it must hold for the quarks in baryons as well.
And the restriction yields two important results:
1) My one and only candidate for Dark Matter (mind the capitals): the black glueball. See The only clue for Dark Matter (...) in the column at the right at page 2 of THE EXPANSION OF THE UNIVERSE, and/or see Fig 3.9 and subsequent explanation below in paragraph Other colorshifts and mesons
at page 3 of QCD.
2) The electron as black quark (and the positron as white quark), see paragraph Electrons as Baryons at page 4 of QG.
While the Minus Sign Go Wild approach yields exciting results but little or nothing that explains other well-known things in our universe.
Therefore I consider Minus Sign Go Wild as to be a previous attempt.
30 September 2023
The gluonic Higgs mechanism provides a way to understand the existence of gluon-gluon reactions a little better. To me it was always a little uneasy to imagine how two lightspeed particles can react. Neither of the particles has time elapsing, so there seemed to be no frame where the reaction can take its space and time. As far as I can see, we only had the quantum mechanical way of thinking
. At a certain moment the state of two lightspeed gluons (call them gluon 1 and gluon 2) superposes with the state of a gluon number 3 (the merger). As it comes to observation then in some cases the two lightspeed gluon state will be chosen again, in the other cases the merger state will be the one. That's without specifying a mechanism how the two-gluon state passes to the merger state. Maybe the following provides such a mechanism.
Gluon 1 has no mass, neither has gluon 2. But when gluon 1 and gluon 2 are at about 0.9 fm mutual distance, then color force is at maximum (see The proton at page 4 of QCD). For one single moment the gluons form a pair. There are two colors together and the gluonic Higgs mechanism sees its chance to work. The gluons didn't see each other, but the vacuum does. For one moment both gluons of the pair get mass. For that single moment both gluons haven't lightspeed any longer. They have time to react and so they do. The resulting merger gluon number 3 is massless again as gluons are, and immediately gains lightspeed. So the gluon-gluon reaction only takes place via the gluonic Higgs field, at high energy that is.
Mind the gluon is pictured as a ring in paragraph The proton
, page 5, QCD. Then there is one orientation that has the largest chance for the Higgs mechanism to work: when the rings are parallel, centered around the same axis and at a mutual distance of about 0.9 fm.
If the two gluons 1 and 2 don't see each other, why a gluon from the vacuum and gluon 1 then will? The vacuum consists of the superposition of gluon fields of all possible states, amplitudes, phases and velocities in all possible directions. Among them is the state that is identical to gluon 1. Those then would see gluon 1 and merge with it. I hope.
The pop-up frame Quaternion units as Pauli matrices indicates that the color of each gluon consists of two Pauli matrices (except for -1).
Four quarks in the shell at page 5 of QCD (next page 43 in TONE) indicates that each gluon consists of two quarks, massless coinciding.
Can we identify each of the two Pauli matrices of a gluon with one of the two quarks the gluon consists of?
 O
O

 NVESTIGATE
NVESTIGATE
Except for -1. The -1 color of the gluon consists of at least 4 and maybe more likely 6 Pauli matrices. That would be 2 or 3 gluons respectively in a composite, a glu2on or glu3on. Those particles maybe only appear at high energies. But then the gluonic Higgs mechanism works, giving our -1 gluon composite mass. (5.1)
If we say that a color +1 gluon passes the time border, what does this mean? There are two ways for this expression to get meaning. See also paragraph The time border at page 7 of storyline FORWARD BACKWARD TIME DIRECTION.
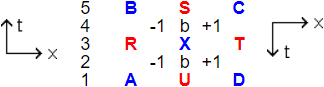
The line of b's is the time border - hidden behind the letters S, X and U there is another b. Not to scale. Colors don't move over larger distances than a few fm, so normally that's the scale of a color scene. But these are colorless colors +1 and -1, therefore ABCD may contain just one vacuum particle as well as encircle a large group of galaxies.
(6.1)
First, if they send what is to them a color +1 gluon toward the time border along CX (from C to X), then a color -1 gluon (that is a +1 gluon from their world enveloped by a tiny parcel of backward time evolving vacuum) is drawn from our matter at A and goes to the same spacetime point X at the time border. Both line segments are in line with each other, together precisely forming one single line through the time border without a kink. The drawing at A is as such that at X wavefunction AX and the wavefunction CX suit perfectly to each other (same amplitude and phase).
Second, if the time border itself at X radiates a color +1 gluon to them at D and a color -1 gluon (that is a +1 gluon from their world enveloped by a tiny parcel of backward time evolving vacuum) to us at B.
If at X the wavefunction of AX suits perfectly to the wavefunction of XB, then there is a third possibility, combining the previous two. The situation then can be regarded as a rebound of both particles from the time border: their +1 goes CXD while our -1 goes AXB. The source particle is their +1 going CX, while our AX -1, XB -1 and XD +1 all three are drawn into existence by the CX.
If so, then a gluon never really passes the time border. It would avoid the question how a +1 color of a gluon, according to pop-up frame Quaternion units as Pauli matrices consisting of 2 Pauli matrices, could convert into a -1 color gluon, consisting of 4 or 6 Pauli matrices. As we observe it, the two matrices of the gluon when it is at their side of the time border multiply dark.
The -1 color at our side of the time border is a +1 color in a tiny sphere of backward time evolving vacuum, enveloped by a time border. And within that time border the two matrices of the two quarks in the -1 glueball still multiply dark. Should we set equal the two dark-multiplying matrices of color -1 with the four or six bright-multiplying matrices of color -1?
 O
O

 NVESTIGATE
NVESTIGATE
The vacuum particles ( i -i ), ( j -j ) and ( k -k ) don't have a time arrow, unlike their constituent gluons. In contrast to of course ( 1 1 ) and ( -1 -1 ) that as to speak ARE the time arrow. (6.2)
The 1's in ( 1 1 ), and the -1's in ( -1 -1 ) too, have same time direction. So the Higgs mechanism works between them. It is nice that the mass of vacuum particle ( -1 -1 ) is explained now but now it is a problem how ( 1 1 ) stays massless. (6.3)
 O
O

 NVESTIGATE
NVESTIGATE
Another example. Take in mind a vacuum particle ( i -i ). For convenience, look at the vacuum particle as if it is a meson with quarks of colors i and -i, but then gluons of color i and -i instead of the quarks. The i is at B and the -i is at D, see spacetime diagram below. When the Higgs mechanism is at work as described in table (2.6), and a pair of gluons like ( k ) ( k ) or ( -k ) ( -k ) appears at X with the intention to give the i and the -i mass, then i absorbs one ( k ) while -i emits the other ( k ) as it is observed by us, forward time people. So, as long as i and -i remain within their time borders, the composite of the two remains massless.
Emitting towards the Higgs field is gaining mass too - backward time evolving mass.
Between the two gluons i and -i in our vacuum particle it looks to us as if just one gluon goes DXB from the -i to the i (instead of ( k ) going to i and the other ( k ) going to -i). But it isn't, not completely. In fact both ( k ) are created at the time border and both go from X at the time border to their goal, as observed in their respective local frames. (6.4)
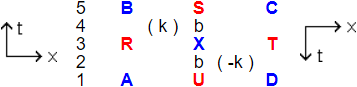
SbXbU is the time border, hidden behind the letters S, X and U there is another b.
Chosen is to represent the particles as they are locally observed. The color -i at D as we observe it, would have been denoted as an i at D. The gluon ( k ) at their side is by them observed as ( -k ). Since i and k are colors, the scale of the figure is a few femtometer.
(6.5)
Regard the storyline FORWARD BACKWARD TIME DIRECTION, especially page 6 and 7 - but it's difficult to grasp the idea when starting at page 6 or 7. One better starts at page 3.
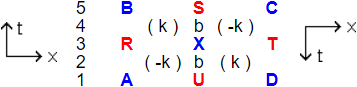
Just another spacetime diagram.
(6.6)
Conclusion 3.6) from the end page of chapter 3 of the TONE storyline is: A Gell-Mann matrix (a gluon) is a kind of Pauli matrix. In QQD each gluon color is the product of TWO Pauli matrices. Except for -1 that needs 4 or 6 Pauli matrices.
How does this work out near the far away time border between a galaxy cluster and an antimatter galaxy cluster?
 O
O

 NVESTIGATE
NVESTIGATE
Two gluons of opposite sign are e.g. i -j, or j -k, or i -i. (7.1)
The conjecture is:
Two gluons of opposite sign will pass each other by or stay put to each other and form a composition, as if they don't react with each other, because the time border is between them. (7.2)
In paragraph Four quarks in the shell at page 5 of QCD (the next page of TONE) is used more than once that they do react with each other, although everytime that two gluons of opposite sign multiply, also the reversed order is multiplied. But then again, the quark and antiquark that make up the gluon are supposed not to react, just like the e+ and e- in the photon don't react with each other in paragraph The color of the photon at page 5 of NET FORCE IN QED. And when the colors of the quark and the antiquark don't react with each other, then also the colors of a gluon and the anticolor of what must be defined as an antigluon don't react with each other.
Obviously, when a multiplication of two gluons of opposite sign is superposed with the reversed order multiplication, it is the same as not reacting with each other. E.g. (5.5) from Four quarks in the shell:

 = -j * i = k =
= -j * i = k = 

 = i * -j = -k =
= i * -j = -k = 
and the superposition of  and
and  yields zero, k -k = 0. (7.3)
yields zero, k -k = 0. (7.3)
Statements (1.4), (1.5) and (1.6) at page 2 of EXPANSION OF THE UNIVERSE mean that in areas where time goes forward the gravitational mechanism works and bright rules are applied; in areas of backward time evolution the gravitational mechanism takes place in reversed time direction (as observed by us) and we see the dark multiplication rules to work there. *)
---
Between antimatter particles work dark multiplication rules. When two anticolors -j and -k of two antiquarks react -j * -k and -k * -j, then the minus-signs multiply according to the dark rule - * - = -. So -j * -k = -i and -k * -j = i. The superposition is i -i = 0.
The reaction -k * k consists of half matter and half antimatter. In the bright multiplication rules it is -k * k = 1, in dark multiplication rules it would be -k * k = -1.
-k * k =
[ DARK -k ] * [ BRIGHT k ] =
[ DARK 1 * k ] * [ BRIGHT 1 * k ]
Here DARK 1 * k = -k according to dark multiplication rule 1 * 1 = -1. (7.4)
But how to interprete the multiplication sign in between the two expressions in brackets [ ] ? As far as I can see, there is no decision ground.
Since there is no decision ground, shouldn't the result be neither 1 nor -1? In our vacuum k is just a particle, but in our vacuum there is a time border around the -k. Two particles at opposing sites of a time border is investigated in the previous paragraph The time border and the gluon of color 1 (the previous paragraph on this page) and discussion about it is not yet settled. (7.5)
---
When an u-quark of color k and an anti-u-quark of color -k approach within their time borders, their mass absorption and emission cancel and the assemblage gains lightspeed: a gluon has formed. Time stands still on the gluon, because of the lightspeed. So the decision whether the multiplication in k * -k is bright or dark is avoided. (7.6)
In the first paragraph The proton of page 4 of QCD is stated that the force between quarks that are very near to each other, is zero, which seems to fit in with decision avoidance. Although that statement is about the force between matter quarks only, or antimatter quarks only. No time border around there.
Item (2.4) in paragraph Meson exchange at page 4 in QCD says: Let us assume the virtual color-anticolor pairs in the shield of a quark can be gluon pairs as well as quark-antiquark pairs.
The emerging quark and its antiquark are each others opposite, as well as the two gluons from an emerging pair are each others opposite. Their elapse of time is opposite, that is our assumption. So to fit in with everything else, we are forced to assume that single gluons, despite their composition of two quarks of opposing time direction, still have a time direction. The photon has no time direction, but the gluon has, because of its color.
1, i, j, k go forward in time and are gluons,
-1, -i, -j, -k go backward in time and are antigluons. (7.7)
According to the first lines in The time border at page 7 of FORWARD BACKWARD TIME DIRECTION, -i, -j, -k and last but not least -1 are just respectively i, j, k and 1 in backward time evolving vacuum, in vacuum as they see it. There the color 1 consists of two Pauli matrices. When the i, j, k and 1 from the backward time evolving vacuum happened to dwell here, we see them enveloped by a time border and to us they appear now as -1, -i, -j, -k. We experience their 1 as a -1 and there is no pair of Pauli matrix multiplication yielding -1. I am forced to assume that the two Pauli matrices the -1 consists of, react dark, as observed by us. **) (7.8)
---
Multiplication order as time order of interaction, see paragraph Physical interpretation of multiplication order at page 3 of QQD, gives that reversing multiplication order is reversing time order, is reversing the elapse of time.
if you have two Pauli matrices in multiplication, then changing multiplication order has the same effect as changing multiplication rules (from bright to dark, or from dark to bright) (7.9)
Changing multiplication order of the Pauli matrices that constitute one color, takes one step in time. As long as the gluon moves at lightspeed, it does not have that time. Only when arriving at another color, when something happens there, there is at least 10^-23 sec of time to eventually change multiplication order of Pauli matrices. I guess in most cases both multiplication orders superpose.
---
When considering a region with a time border somewhere in it, then at one side of the time border Higgs mass is absorbed from the vacuum, while at the other side Higgs mass is emitted towards the vacuum. The net mass absorption/emission of the area determines its net mass. When an i quark and a -j antiquark react and those quarks have different magnitudes for their mass (e.g. in case of an u-quark and an anti-d-quark, I guess it must be the different sizes of their electric charge that gives the difference in mass) does their reaction i * -j and -j * i work out bright or dark? Mark this doesn't occur in nature, where only play a role: i * j * k (baryons), -i * -j * -k (antibaryons); i * -i, j * -j, k * -k (mesons), so decision is avoided. It plays a role in Fig. 3.3 at page 3 of QCD and (the same Fig. 3.3) in paragraph Multiplication order at page 3 of QQD, but there both multiplication order superpose to a net result of zero.
---
Does time symmetry play a role? Regard k and -k as two particles, moving about as large masses do, larger than e.g. the electron mass, take e.g. a proton mass. Suppose we start with k and -k at rest relative to each other at sufficiently small mutual distance. Suppose as a consequence of the color force, k and -k recede from each other in the first instant, in doing so constituting a repulsion. In the backward time evolving world this is observed as an approaching of the k and -k followed by a stay put, which is also to be interpreted as a repulsion. So no contradiction appears so far. Ditto for attractive behavior. See also item 3 at page 1 of FORWARD BACKWARD TIME DIRECTION.
A combined occurence of approaching first and then receding again would be time symmetric but would constitute a bounce off.
In case of a bounce off caused by repulsion (particles approach each other while decelerating until minimal distance, then recede and accelerate again) the bouncing-off particles remain a longer time around the smallest mutual distance than in a bounce off caused by attraction (particles approach while accelerating until minimal distance, then recede and decelerate again). A repulsive bounce off takes a little longer time than the corresponding attractive bounce off, time in which other forces get a little more chance to work. This is a fundamental asymmetry between attraction and repulsion, if one may treat the particles to move about as larger masses do. ***) (7.10)
Suppose the initial relative velocity of the approaching k and -k is too small. When the k and -k attract each other, this leads to a bound state of k and -k. While when k and -k repel each other, a bound state is no option.
 O
O

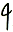 NVESTIGATE
NVESTIGATE
 O
O

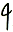 NVESTIGATE
NVESTIGATE
A previous attempt
Would it be worth considering Pauli matrices not only to determine color but also determining spin? Then when one multiplication order is forbidden (because yielding e.g. -i) then also one spin is forbidden, e.g. spin down, which is the hallmark of the weak force in case of neutrinos. No, spins are rotations in the complex space (1 and i), while quaternion units are rotations in the 1ijk space.
Another previous attempt
The conjecture proposed in (5.1), just below paragraph Quark mass at page 4 of QCD, is considered now as a previous attempt.
If a real quark absorbs only the spin of one of the two gluons of a vacuum marble, then that vacuum marble can merge to a white gluon, a white glueball, according to i * -i = j * -j = k * -k = 1 * 1 = -1 * -1 = 1, see (2.3) at previous page. The real quark undergoes a spontaneous spin swap.
real quark, spin 1/2  + spin 1
+ spin 1  --> real quark, spin 1/2
--> real quark, spin 1/2 
vacuum particle ( gl  gl
gl  ) --> real glueball gl
) --> real glueball gl 
The vacuum is reduced by the volume of 1 vacuum particle and a real glueball appears. Space converted into matter. The energy in the white glueball must equal the energy that can be assigned to the volume of the (now) empty spot, leaved behind by the disappeared vacuum particle. This defines the energy of 1 m3 of vacuum. Space is energy. And that energy must equal the energy of the amount of sagging-in of the field that embodies gravity. (8.1)
Then the process itself neither yields nor costs energy and will be as frequent in forward time direction as in backward direction, ensuring vacuum to be stable. Backward direction means a white glueball splits into two white glueballs and obtains the extra spin from a nearby quark, after which the vacuum absorbs the newly formed vacuum marble.
Then the vacuum around a quark is superposed by white glueballs. The quark is immersed in a sea of virtual white glueballs.
Spin is not conserved in this reaction as it is stated here. The real quark shows an extra +1 spin and the appearing real glueball shows another +1 spin to the system. So what next? Assign the missing spin to the vacuum? Net vacuum spin is not defined yet.
July 2023
Violation of spin conservation causes the reaction not to occur. But the example is illustrative. The possibility to estimate the energy stored in one m^3 of vacuum is tantalising.
White glue1balls can be formed when the quarks of a proton emit 2 gluons simultaneously, as in Fig 3.4 and Fig 3.11 at page 3 of the storyline QCD. When the two gluons form a glu2on, a glue2ball in this case, instead of merging, then the pair can be absorbed by the vacuum, enlarging the vacuum with the volume of the pair (after which rearrangement of the vacuum marbles is taking place, restoring flat space). Mark two gluons don't merge easily because of the spin (see gluNons at page 7 of QCD), so merging is not the first thing to be expected.
The creation of black gluons is worked out in Fig 3.9 and Fig. 3.10 and the explanation between these two figures, in the paragraph Other colorshifts and mesons at page 3 of QCD. Black gluons might form pairs eventually, but those are not absorbed by the vacuum because of (2.7), (2.8) and (2.9) from the previous page. It is the well-known creation of a massive two particle composition.
 gl
gl  (spin +2) and a glue2ball field gl
(spin +2) and a glue2ball field gl  gl
gl  (spin -2). *)
(spin -2). *) = spin +1 and
= spin +1 and  = spin -1.
= spin -1. gl
gl  and a glue2ball field gl
and a glue2ball field gl  gl
gl  (both spin 0). The vacuum that is the 3rd Higgs field Higgs field is taken to consist of
(both spin 0). The vacuum that is the 3rd Higgs field Higgs field is taken to consist of  gl
gl  absorbs a graviton gl
absorbs a graviton gl  gl
gl  . Three gluons merge easier than two gluons, as is argued at page 7 of the QCD storyline. I tried to work out the gluNon concept at that page. You can read that later if you take for granted that 3 gluons merge easier than 2 gluons. And that 2 gluons can form a glu2on, a composite made of 2 gluons that merge at least not immediately. When the glu2on is colorless I call it a glue2ball.
. Three gluons merge easier than two gluons, as is argued at page 7 of the QCD storyline. I tried to work out the gluNon concept at that page. You can read that later if you take for granted that 3 gluons merge easier than 2 gluons. And that 2 gluons can form a glu2on, a composite made of 2 gluons that merge at least not immediately. When the glu2on is colorless I call it a glue2ball. , spin +1) + ( gl
, spin +1) + ( gl  gl
gl  , spin -2) --> ( gl
, spin -2) --> ( gl  , spin -1) (1.1)
, spin -1) (1.1) , spin +1) is one of the two gluons from gl
, spin +1) is one of the two gluons from gl  gl
gl  . The other gluon from the pair gl
. The other gluon from the pair gl  gl
gl  remains unaffected. The disappeared graviton leaves an empty spot at the place it had occupied. So the two gravitons change into one empty spot and one Higgs particle of same volume (is assumed) as the graviton:
remains unaffected. The disappeared graviton leaves an empty spot at the place it had occupied. So the two gravitons change into one empty spot and one Higgs particle of same volume (is assumed) as the graviton: gl
gl  + gl
+ gl  gl
gl  --> gl
--> gl  gl
gl  + empty spot (1.2)
+ empty spot (1.2) gl
gl  is absorbed at the coupling of some particle in the course of renormalization, leaving another empty place there.
is absorbed at the coupling of some particle in the course of renormalization, leaving another empty place there. gl
gl  as vacuum particle while the other, gl
as vacuum particle while the other, gl  gl
gl  , could be real. We need them both as vacuum particles.
, could be real. We need them both as vacuum particles. gl
gl  and one gluon in graviton gl
and one gluon in graviton gl  gl
gl  would just interchange their spin, one gets gl
would just interchange their spin, one gets gl  gl
gl  and gl
and gl  gl
gl  , which are two Higgs particles. Now there are two Higgs particles created in one single strike to be absorbed in the course of renormalization. This is thought to take place at the location of a quark, the quark mediates this spin conversion.
, which are two Higgs particles. Now there are two Higgs particles created in one single strike to be absorbed in the course of renormalization. This is thought to take place at the location of a quark, the quark mediates this spin conversion. gl
gl  or gl
or gl  gl
gl  . So 8 fields altogether. (2.3)
. So 8 fields altogether. (2.3) gl
gl  . The conversion in which the Higgs particle was created, is thought to take place at the location of a quark, the quark mediates this spin conversion. Take in mind a baryon, three quarks together. If this conversion also detaches the gluons from each other, then you have two independent gluons of opposite color. Then one gluon can go to the second quark and the other to the third quark.
. The conversion in which the Higgs particle was created, is thought to take place at the location of a quark, the quark mediates this spin conversion. Take in mind a baryon, three quarks together. If this conversion also detaches the gluons from each other, then you have two independent gluons of opposite color. Then one gluon can go to the second quark and the other to the third quark. gl
gl  ) Higgs particle --> (gl
) Higgs particle --> (gl  ) (gl
) (gl  ) two independent gluons (2.4)
) two independent gluons (2.4)
 , a d-quark with anticolor -i. Let's just take the 3 quarks in the baryon to have color i, j and k and whatever plus or minus signs are in front of them, their multiplication always will yield the colorless +1 or -1 end state, that thus is permitted. So let's go on with the baryon with colors j -i k, or in (2.8) with -j i k. This way of treating colors is what is called
, a d-quark with anticolor -i. Let's just take the 3 quarks in the baryon to have color i, j and k and whatever plus or minus signs are in front of them, their multiplication always will yield the colorless +1 or -1 end state, that thus is permitted. So let's go on with the baryon with colors j -i k, or in (2.8) with -j i k. This way of treating colors is what is called 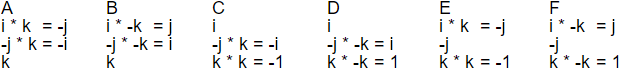

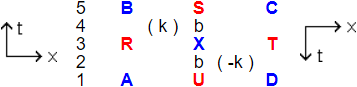
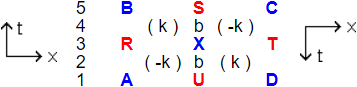

 = -j * i = k =
= -j * i = k = 
