Filling in the vacuum marbles

A particle traversing the vacuum acts as if it doesn't react with the vacuum. The vacuum is chosen to consist of vacuum marbles, vacuum particles. According to (3.02) at page 3 of QQD, IF the particle reacts (couples) with the vacuum by color force, then the wavefunction F of the particle times a vacuum particle must equal F, so the vacuum particle must be 1 (the quaternion 1).

F * 1 = F             (2.1)

In paragraph Massless coinciding at page 2 of THE EXPANSION OF THE UNIVERSE we found three massless compositions. We constructed the gluon from a quark and an antiquark, the photon from an electron and a positron, and the neutrinophoton from a neutrino and its antineutrino.

Particle	Spin	Treated at	TONE page
the colored gluon	1	this page	41
photon	0	page 5 of NET FORCE IN QED	23
neutrinophoton	0	page 4 of this storyline	44

 
We are going to fill in the vacuum marbles with these three particles.
 

 
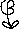
We start with the most complicated one, the gluon. Since we don't observe the vacuum to have color, it is concluded the vacuum particles cannot be colored. Since we stated that we start with colored gluons, the only possibility for vacuum particles are colored gluon pairs from which the colors abolish each other.

According to accepted QCD the gluon has color charge, reaction time of 10^-23 sec and spin +1 or -1. In my description the gluon gets a fourth property: it embodies a tiny bit of space. *) For every strong force reaction of quarks, 10^23 times per second, one vacuum marble is absorbed from the vacuum to give the quark its mass, and along with it a tiny bit of space disappears. In the pop-up frame radius of the Higgs boson the relative distance of the vacuum marbles is calculated to be about 10^-21 m.

*) Here it would suffice to assign a tiny bit of space to the gluon pair, not specifically the colored gluon.

So the vacuum can consist of gluon pairs that are 1. If so then each quark of the proton reacts with the vacuum 10^23 times per second (typical strong force reaction time), in each reaction absorbing a vacuum marble, thus causing the tiny gravitational field of the proton, according to the mechanism described in the previous page.

Gluons that are 1 are called glueballs, a glue1ball in the view of GluNons, page 7 of the storyline QCD. But colorless gluons don't glue, the vacuum they form will not cohere. So it must be colored gluons, i, j, k, -i, -j or -k, these gluons glue, gluing 3 dimensional space together. But there is no color in the vacuum. When there was, like the color i, then F * i = iF which does not equal F no more (i is the quaternion i, not the complex number) . It must be pairs of colored gluons that equal one: i * -i = j * -j = k * -k = 1.

So the vacuum should consists of the gluon pairs ( i   -i ), ( j   -j ) and ( k   -k ).

Gluons are massless. Supposed is the composition of two gluons is still massless, the composition has no net absorption from the Higgs field. Absorption from the Higgs field is worked out further down.

The quaternion units are 1, i, j, k, -1, -i, -j, -k. What seems more natural than to complete the colors of the vacuum with the colorless color pair ( 1   -1 ), a white-and-black gluon pair? But 1 * -1 = -1 * 1 = -1 and so F * -1 = -F. So it is no, the pair does not add to the vacuum superposition. Instead ( 1   1 ) as well as ( -1   -1 ) should add to the vacuum superposition because 1 * 1 = -1 * -1 = 1. We conclude:

The vacuum consists of the pairs ( i   -i ), ( j   -j ), ( k   -k ), ( 1   1 ), ( -1   -1 )           (2.2)

i * -i = j * -j = k * -k = 1 * 1 = -1 * -1 = 1           (2.3)

This in fact is what happens when the i and -i (and likewise j and -j, k and -k, 1 and 1, and -1 and -1) of a vacuum particle would merge. Is ( -i   -i ) in superposition with 1? Just 1, I mean, the colorless color 1? To be frank, I expect this not to happen. I always assumed the two gluons of a vacuum particle do coincide but do not merge.

The net color sum of the pairs with color within neatly adds up to zero:

i	-i	= 0
j	-j	= 0
k	-k	= 0	(2.4)

This is what happens when e.g. i and -i coincide but do not merge, what I did expect to happen in vacuum particles so far. 0 is not a quaternion unit, 0 is not a color. So the vacuum is colorless.

But in the pairs ( 1   1 ) and ( -1   -1 ) the colors add to two: 1 + 1 = 2 and -1 -1 = -2. This is colorless (no i, j or k) but not valueless. What does this mean? Is this the arrow of time? Its length?           (2.5)

A proton reacting with the vacuum pair ( 1   1 ) then is F * 1 * 1 = F. Any reaction with a vacuum marble is also one step forward in time, as is argued in the last paragraph of Quark mass at page 4 of QCD.
 

Building vacuum from gluons

We are trying to build spacetime from particles that are governed by Feynman-diagrams. The horizontal bottom-line of Feynman diagrams, where the situation starts with, are particles in free flight. That's all there is to a single Feynman diagram: particles with constant speed going from coupling point to coupling point. There are no accelerations in Feynman-diagrams, accelerations are a build-up effect of a large number of small velocity increments or decrements, small velocity jumps.

To be frank, when going from coupling point to coupling point it does so along all possible routes through spacetime. In fact Feynman-diagrams in Feynman-diagrams in Feynman-diagrams ad infinitum.

When the vacuum consists of bosons - fundamental or composite - then a next such boson will perfectly align with the already present vacuum bosons (laser-effect). The boson will be absorbed by the vacuum, it will disappear while the vacuum expands by the volume of the boson.

When the vacuum consists of fermions - fundamental or composite - then a next such fermion will occupy the next available state and thus disappear too, making the vacuum expand by its volume. There always is another state, the number of states is infinite (Dirac sea).

We have chosen to fill in the vacuum marbles with gluons. We have also chosen to fill in the vacuum marbles by photons, see The electron-positron photon Higgs field at page 5 of the storyline QED. And in paragraph Neutrinophotons at page 4 of this storyline QG we are going to fill in the vacuum marbles with neutrinophotons, particles made of a neutrino and an antineutrino massless coinciding. Three vacuum fields, three vacuums in fact. All vacuum fields are liquid bose condensates.

Let's call the vacuum marbles filled in with gluons the gluonic vacuum or hadronic vacuum.

The vacuum consisting of photons then will be the photonic vacuum or leptonic vacuum.

And what name for the vacuum of neutrinophotons? The neutrinophotonic vacuum I suppose.

Photons and neutrinophotons as well, react at least 1000 times slower than gluons. So the vacuum will for 99.9 percent of the time be reigned by gluon reactions and only 1 out of 1000 times by an additional vacuum photon reaction. So if we talk about THE vacuum it is the gluonic vacuum, the hadronic Higgs field.

 
Real axis -------- not shown.
 

The vacuum particles of (2.2), do they have antiparticles? We construct the antiparticles by replacing every gluon in (2.2) by its opposing color, i by -i, j by -j, k by -k and 1 by -1, or the other way around. It is the same as multiplying every particle by -1.

( -i   i ), ( -j   j ), ( -k   k ), ( -1   -1 ), ( 1   1 )        (2.6)

which happen to be precisely the same particle pairs as in (2.2). The vacuum particle pairs are their own antiparticle, like the photon. We have chosen the photon to consist of an electron an a positron massless coinciding within their time borders. Photons don't annihilate each other nor themselves, despite they are their own antiparticle.

There are two ways now to proceed.

First way

The black glueball is the only gluon with mass.         (2.7)

Then the pair ( -1   -1 ) would consist of two massive gluons NOT canceling out each other's mass within their time borders, since the constituting -1's have same time direction. The ( -1   -1 ) pair would be ruled out as vacuum particle, leaving only 4 particles as vacuum particles:

( i   -i ), ( j   -j ), ( k   -k ), ( 1   1 )         (2.8)

Second way

The black glueball on itself is massless, but when two together they gain mass. This is worked out in The quaternion approach at the next page.         (2.9)

Yes, that would do! And then the difference between forward and backward time evolving vacuum can be given feet on the ground now. As observed from us the backward time evolving vacuum consists of:

( i   -i ), ( j   -j ), ( k   -k ), ( -1   -1 )         (2.10)

As observed by us, forward time people, (2.9) is a massive vacuum, a vacuum with a massive component. The energy for that is not available. So in our vacuum (2.9) will not occur, only (2.8) will. Therefore time will run forward only. The secret of time.

The essence of time is in the hadronic vacuum.         (2.11)

The backward time vacuum is not massive as it is observed by the backward time evolving people there. Their vacuum equals eq. (2.8), as they themselves would write it down. Observed from us not only (2.9) holds, but the multiplication rules are different there too, see Dark multiplication rules below.

The vacuum particles from the vacuum superposition are no longer all their own antiparticle then. (2.8) are the antiparticles of (2.9) and vice versa. Moreover, multiplying (2.8) with -1 (the time-reversing factor) yields (2.9), multiplying (2.9) with -1 yields (2.8) again.

A massless ( 1   1 ) vacuum marble can convert to a massive ( -1   -1 ) by black glueball exchange, compare Quaternion application 4 at page 7 of QQD. This is a forbidden conversion since the energy for massive vacuum is lacking.         (2.12)

Multiplying

( i   -i ), ( j   -j ), ( k   -k ), ( 1   1 )        (2.8)

by -1 in fact yields

( -i   i ), ( -j   j ), ( -k   k ), ( -1   -1 )

which is (2.9) stated a little more precise.

When a vacuum particle is a shape, an object, and 1ijk space is xyzt spacetime, then all four coordinates of that object will change sign when multiplying by -1. The time swap makes it run backward in time. The first two space dimension swaps will cancel each other. The third space dimension swap changes the object in its enantiomer, its mirror image.         (2.13)

For 1ijk quaternion space = xyzt spacetime, see paragraph The real-imaginary swap at page 4 of of QQD and (5.4) up to (5.7) at page 5 of QQD.

One single particle has its structure, its shape, relative to the vacuum. Take in mind e.g. its spin. If we observe that (a part of) vacuum itself is mirror-imaged, I assume the shape of a single particle in that part of vacuum is mirror-imaged along with it, not noticing something had changed. But we see its spin has swapped. Spin is connected to space, spin is a structure.

Swap of the sign of the time coordinate makes the spin of the particle to reverse. Changing the particle in its enantiomer swaps the spin back again. The spin of a particle that is residing in an area of vacuum particles that are multiplied by -1 as in (2.13), doesn't change.         (2.14)

Dark multiplication rules

The time border is the mathematical border between forward time evolving vacuum and backward time evolving vacuum. Conjectured is that the computation rules at both sides of the time border are different.

Our computing rules are:

1 * 1 = -1 * -1 = 1

1 * -1 = -1 * 1 = -1           (9.20)

Regard the two vacuum pairs ( 1   1 ) and ( -1   -1 ). We assume multiplying by the time reversing factor -1 yield these vacuum pairs in backward time evolving vacuum; which turned out to be the same 2 pairs.

-1 * ( 1   1 ) = ( -1   -1 )

-1 * ( -1   -1 ) = ( 1   1 )

Applying ( 1   1 ) means * 1 * 1. Applying ( -1   -1 ) means * -1 * -1.       (a)

Assumed is a backward time evolving vacuum pair equals -1.       (b)

(a) and (b) together forces us to set equal * 1 * 1 = * -1 * -1 = -1.

OR this is nonsense, OR this means their sign multiplication rules, as observed by us, are:

DARK       -1 * -1 = 1 * 1 = -1

DARK       -1 * 1 = 1 * -1 = 1           (9.21)

The prefix DARK meaning: valid only in backward time evolving vacuum.

Swap all signs in one set of rules, that gives the other set. Another way of stating this is: start with our rules and multiply every single factor with -1, this gives their set. Multiplying with -1 reverses time direction. When they multiply every factor with 1 according to their rules, one gets our set back again. As observed by us, 1 is the factor that reverses time in their world.           (9.22)

One states also:

 
DARK       -i * -i = i * i = 1

DARK       -i * i = i * -i = -1           (9.23)

In the last line one recognizes the vacuum marble pair ( i   -i ) yielding -1, the backward time evolving vacuum as observed by us.

 
DARK       1 * i = -1 * -i = -i

DARK       1 * -i = -1 * i = i         (9.24)

 
DARK       = =         (9.25)

				s1	s2	s3
		s1		-1	-i	j
		s2		i	-1	-k
DARK		s3		-j	k	-1		(9.26)

(9.26) means DARK s1 * s2 = -i, DARK s1 * s3 = j, and so on. For the Pauli matrices s1, s2 and s3, see Pauli matrices at page 9 of QQD.

There is little difference between forward time vacuum and backward time vacuum. Time goes backward. The neutrino field swaps spin. The multiplication rules swap sign.

Dark Mechanics

I have hardly tried yet to implement dark multiplication rules on Newtonic mechanics. One of the first tries should be the following two equations.

1)   F = m * a

(1rst law of Newton)

F Force, m mass, a acceleration
 

2)   G * m1 * m2 / r = -m1 * v / r1

(left side of eq. gravitation law of Newton, right side of eq. centrifugal force)

G gravitational constant, m1 mass 1, m2 mass 2, r distance between mass centers of mass 1 and mass 2, v velocity of mass1, r1 distance from mass center of mass 1 to mass center of the system m1 + m2.

For m2 = mass of the Earth (very large mass) and m1 = mass of a satelite like the ISS (comparatively quite small mass) one usual set equal r = r1. The equation becomes then

G * m2 / r = -v

To begin with, the mass, should that be taken negative? According to (the 3rd alinea of) paragraph The electron-positron photon Higgs field at page 5 of NET FORCE IN QED, yes. So we write -m1 * -m2. Because - * - = - this is equal to (yet to find out)

And G, the gravitational constant?