The Higgs field
Let's first set up the scenery. Let's start with the vacuum. The undisturbed vacuum - without gravitation that is - is proposed as a non-curved grid of solid marbles, a solid grid of vacuum particles. Static, standing-still marbles, stacked upon each other as the marbles of a child play in a box. No, to begin with we better start as the atoms in a Na-Cl grid (cubes), a Cartesian grid. Or like a box from top to bottom neatly stacked with oranges (tetrahedrons). No open spaces large enough to fit another marble; no marble overlap. Constant total volume of all the marbles together.
When at motion with respect to such a marble field, because of the Lorentz contraction the field will become denser. To be Lorentz invariant like the vacuum is, the field has to be the superposition of the vacuum particle fields of every possible velocity, the superposition of all grids of solid marbles that only differ a velocity, pervading each other without seeing each other. The solid marble oceans pervade the Earth too. In fact all of Earth, i.g. all matter, is just another superposition to the fields. It is very much like the field of all possible velocities. The field of all possible velocities is invoked at several other occasions, see the listing below at that page.
After the vacuum, our second player is the Higgs field. The Higgs field, the field all massive particles absorb its mass from, pervades all of space. It is tempting to identify the vacuum with the Higgs field, so let's do so and let also the Higgs field consist of marbles. Let's identify the vacuum marbles with the particles making up the Higgs field. The vacuum is built from what we call here Higgs particles.
The field of all possible velocities then opens the possibility that velocity with respect to the vacuum is impossible. It is possible to consider every particle that has mass as standing still with respect to the vacuum it couples to, standing still with respect to the Higgs field from which it absorbs its mass. Particles that have a velocity with respect to us, couple to a different velocity field, a different Higgs field, than we do and with respect to that field they stand still. Coupling to standing-still field, absorbing from standing-still field, absorbs least energy and is most abundant. This fits in well with the view of the vacuum as a grid of marbles wherein the particle is standing still, a view that is used below.
Let's take the Earth, a formidable collection of particles floating free in the vacuum, as third player. The solid marble grids pervade the Earth too. At a coupling, one of the particles of the Earth absorbs a Higgs particle (what we call here a Higgs particle), necessary in the course of renormalization. When a particle absorbs mass from the Higgs field, it absorbs one vacuum marble, one Higgs field particle. The particle absorbs the Higgs particle from the Higgs field relative to which it is standing still. (Take the rotation of the Earth to be absent.) The marble of that Higgs particle disappears, leaving an empty spot, a hole in the vacuum. Pressure from the outside
forces the marbles around the hole to fill in the empty spot, to fall into the hole
. In doing so they leave behind new holes, all new holes together equalling precisely the volume of the first hole. The particles next to the new holes falls into them, leaving behind them still smaller holes, and so on. The vacuum streams. Was the vacuum first resembling a solid grid, now it looks more like a fluid, an ocean of solid marbles. Effectively the volume of the empty spot displaces spherically to the outside, without changing volume dividing itself over an area that increases with the square of the distance to the absorbing spot. The empty spot, originally spherical, now forms a shell of missing vacuum. The volume of the shell is its surface times its thickness.
In fact the vacuum marble field sags spherically into the hole of the disappeared Higgs particle. The vacuum marbles never overlap and seek being stacked upon each other again, no space to fit another marble. The displacement of a shell of vacuum marbles onto an already sagged shell just below is inversely proportional to the surface of that shell, is inversely proportional to the square of the distance to the absorbing spot. When the surface is twice as large, the distance over which is sagged in, is twice as small.
Now we yet only have to state that the displacing Higgs field drags along with it all masses that are floating
in it. The dragging is 100 percent. The masses are considered to stand still with respect to the displacing vacuum marble field and keep it like that. This is gravity, the gravitational field in action, our fourth player. The vacuum is the Higgs field is the gravitational field.
According to the Newton gravitational law the gravitational force is inversely proportional to the square of the distance to the gravitational center. As argued, the Higgs field displacement is inversely proportional to the square of the distance to the vacuum marble absorbing spot. At any place in the field a force is proportional to the displacement caused by the force:
F = ma, s = 1/2 * a * t , so at any point at one moment t is F
, so at any point at one moment t is F 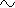 a
a 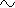 s.
s.
(F = force, m = mass, a = acceleration, s = displacement, t = time, t = t square, F
= t square, F 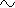 s means F is proportional to s).
s means F is proportional to s).
When mass is doubled then there are twice as much baryons present in the mass, and so the number of couplings per second in the mass is doubled too. The disappearance of Higgs particles doubles and the rate of sagging in of spheres into the hole left behind doubles too. The displacement doubles. So vacuum displacement of the gravitational field is proportional to the mass causing the gravitational field.
It doesn't really have to be marbles; the main point is conserved fluid space. Some volume of space inside matter disappears when Higgs field is absorbed. But all further events act as if space is conserved. The disappeared space - the hole - is filled in with the space around it without any further appearing or disappearing of space. It fits in quite well with the view that the vacuum consists of marbles neatly stacked upon each other. In fact we are going to fill in the marbles with particles that we already know.
The presented view so far accounts for:
1) The fact that all masses at the same time and place in the gravitational field undergo same acceleration.
2) The inversely squared proportionality of the rate of displacement with the distance and the proportionality with the masses.
3) The proportionality of the inert mass (resistance to change of velocity and the E = mc source of energy) with the ponderable mass (mass that causes the gravitational field). When there are 2 times more nucleons, then there are 2 times as much vacuum marble absorptions.
source of energy) with the ponderable mass (mass that causes the gravitational field). When there are 2 times more nucleons, then there are 2 times as much vacuum marble absorptions.
In radius of a vacuum marble the gravitational constant is used to calculate the distance between neighboring vacuum marbles to be about 10^-21 m.
At the next page is shown that the Newtonian gravitational law presented so far resembles a kind of conveyor belt, displacing only at constant pace. It seems to be no force. Next page shows how the gravitational action as presented at this page obeys F = ma, the second law of Newton.