At page 1 of this storyline is stated
 +
+  +
+  =
= 
 +
+  +
+  =
=  (1.3) and (1.4) from page 1
(1.3) and (1.4) from page 1
Mark we placed a color and its anticolor just above each other. White
here means zero
, zero color. It is from QCD where quaternion units play no role.
Previous two pages of this storyline QQD - colors are quaternion units now - indicate that when colors couple, they have to be multiplied.
 *
*  *
*  =
= 
 *
*  *
*  =
=  (1.1)
(1.1)
Mark we did not place a color and its anticolor right above each other. (The reason why will soon be clear.) Well, the green-magenta are, but the others are not. In quaternions  = 1, the 3 colors together (or the 3 anticolors together) must equal 1. When white
= 1, the 3 colors together (or the 3 anticolors together) must equal 1. When white  = 1 then -1 will be black
= 1 then -1 will be black  .
.
What is right, should we sum or multiply? Things turn out as follows.
When particles couple, merge to a merger particle, the colors (quaternion units) of the particles must be multiplied. (1.2)
The data of the separated particles just before merging is lost, e.g. how many particles that were and what kind of particles.
This also holds the other way around.
When a particle decays in two or more other particles, the colors of the particles must be multiplied. (1.3)
Examples:
1) The gluon that is emitted by a quark.
2) A gluon that couples to another gluon.
3) The two quarks coinciding massles to form the gluon, see Four quarks in the shell at page 5 of QCD. This holds as a merger although the 2 quarks never really merged, see paragraph Depicting the model at the same page.
4) The W+ or W- particle decaying into a neutrino and an electron, see The color of the neutrino at page 4 of QG.
5) Two colored gluons coinciding massles to form a vacuum particle, see page 2 of QG.
6) Two spin 0 photons coinciding massless to form a vacuum particle.
7) Two neutrinos coinciding massles to form a vacuum particle, see Neutrinophotons at page 4 of QG.
When the particles stay together - they form a composite but do not merge - their colors sum up (the colors don't multiply then) (1.4)
See paragraph Multiplication order
below, leading to (2.8).
Examples:
1) The 3 quarks in the baryon.
2) The 2 quarks in the meson.
3) The color of the electron and the positron forming the photon when coinciding massless, see The color of the photon at page 5 of NET FORCE IN QED.
There is no practical meaning to the two sums (1.3) and (1.4) from page 1 at page one of this storyline. To perceive a color you have to couple with it and that means at least one multiplication. The sum
 +
+  +
+  = i + j + k
= i + j + k
has no observable meaning. It is just i + j + k in quaternions, you cannot reduce it any further. The equation
i + j + k = 0
would be like when in well known complex numbers you would state
i + 1 = 0
which both are false and meaningless.
What if we experiment a little with the original color sum equation? In a baryon we have red + green + blue = white. We did set red = i, green = j, blue = k, white =1. Then red + green + blue = white becomes i + j + k = 1. This is the quaternion q = -1 + i + j + k. Two baryons colliding then should be the multiplication
(-1 + i + j + k) (-1 + i + j + k) = -2 -2i -2j -2k = -2 ( -1 + i + j + k) (1.5)
What is this, minus two times a baryon? The original two baryons? Why the minus sign?
Try this at the excel document baryoncollision.xls. Two yellow sections next to each other are two colliding baryons. Just fill in the yellow sections of one line, click somewhere else and in the blue section appears the resulting multiplication. (1.6)
Popup Quaternions at the bottom, shows how to mold a matrix multiplication into a quaternion multiplication.
Do quarks couple to each other? According to QCD the answer is no: quarks couple to gluons (emission or absorption) and the gluons then couple to other quarks. In QCD quarks do not couple directly by color force. Why not? Is it the fractional electric charge? Electric charge merger particle = [ +2/3, -1/3 ] + [ +2/3, -1/3 ] = [ -2/3, +1/3, +4/3 ]. This seems strange, but as long as together with the 3rd quark the electric charge remains integer charge, there is not realy an objection. Probably it is the spin. The spin of the merger particle becomes [ -1, 0, 1 ] and that is no longer a quark. Also the taste becomes undefined. What is taste u + u, d + d, u - d, d - u?
Here means [ a, b, c ] = one element out of the set [ a, b, c ] = a or b or c.
What a remarkable situation it is! The colors of the quarks from a single hadron cannot depart from each other nor will they ever merge to one color. I mean, colors can couple to each other when within reach and at 0.7 fm relative distance the strong force is indeed quite strong. So it is quite strange the colors of the quarks within one baryon don't couple. But oke, they don't.
Is there meaning to a white proton p+ attracting a neighboring white neutron n0 in a nucleus? When within reach (less than 2 fm) two quarks from different hadrons do attract each other by their colors. Only colored gluons glue, the gluons i, j, k, -i, -j and -k. The gluons 1 and -1 do couple by color but don't glue. When a colored gluon starts from a quark in the p+ and then leaves the p+, the p+ remains in a colored end state which is forbidden. When the colored gluon arrives at a quark in the n0 then the n0 is brought into a colored end state too which is also forbidden. (1.7)
The only possibilities for gluons between nucleons seem to be reactions that leave the color end state of the nucleons at 1 or -1. A gluon causes a color swap between the quarks it connects. A possible reaction is e.g. a gluon from the p+ red quark to the n0 green quark, simultaneous with a gluon from the n0 red quark to the p+ green quark. This gives two color swaps after which both the p+ and the n0 again have 1 red, 1 green and 1 blue quark. Simultaneous here means within 10^-23 sec. As a result the allowed color reactions between quarks of different nucleons is only a small part of the set of all possible color interactions between those quarks. The demand for colorless end state seems to cause the force between nucleons to be much weaker than the force between the quarks within a nucleon. (1.8)
Remember from the previous two pages:
ij = k, jk = i, ki = j, ji = -k, kj = -i, ik = -j
1/i = -i, 1/j = -j, 1/k = -k
i/j = 1/j * i = -j * i = k (i/j = left multiply i by 1/j)
See popup Quaternions
q * gl (right multiply the quark by the gluon)
A gluon goes from a green quark in the p+ to a red quark in the n0. The gluon then is
 =
=  /
/  = j / i = -i * j = -k =
= j / i = -i * j = -k = 
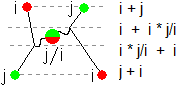 (1.9)
(1.9)
When a gluon goes from a quark in a proton to a quark in a meson passing very nearby then according to QCD it does so along all possible routes. That includes the route going to one of the other two quarks in the proton, couple there and change its color (gluon is absorbed), couple again and changing the color back (gluon re-emitted) and then set for the quark of destination. The whiteness of the proton is tested in between then.
The three quarks in the hadron differ in color. The hadron has one color in common with the meson passing nearby. Quarks are fermions and so the Pauli prohibition holds for them. When the two quarks of same color also have equal spin, electric charge and taste then repulsion is the only option. (1.10)
There is another meaning to the zero sum end state of colors in the next paragraph.
Multiplication order *)
From page 1 of this storyline we find
 *
*  *
*  = i * j * k = -1 (2.1)
= i * j * k = -1 (2.1)
 *
*  *
*  = -i * -j * -k = 1 (2.2)
= -i * -j * -k = 1 (2.2)
 *
*  *
*  = k * j * i = 1 (2.3)
= k * j * i = 1 (2.3)
 *
*  *
*  = -k * -j * -i = -1 (2.4)
= -k * -j * -i = -1 (2.4)
Multiplication order does count in quaternions and (2.2) and (2.3) indeed equal 1. But (2.1) and (2.4) equal -1. One is tempted to define a normal
and a reversed
multiplication order. Let's define the equations (2.2) and (2.3) with outcome 1 as normal order. Then (2.1) and (2.4) with outcome -1 is the reversed order.
normal order








 = k j i k j i k j i
= k j i k j i k j i








 = -i -j -k -i -j -k -i -j -k
= -i -j -k -i -j -k -i -j -k
reversed order








 = i j k i j k i j k
= i j k i j k i j k








 = -k -j -i -k -j -i -k -j -i
= -k -j -i -k -j -i -k -j -i
So when you have the 3 different colors and want them to yield white, you have to choose your multiplication order from the color normal order, kji = jik = ikj = 1. And if you have the 3 anticolors and want them to yield white, you have to choose their order from the anticolor normal order, -i -j -k = -j -k -i = -k -i -j = 1.
ij = k which equals  *
*  =
=  . But also is ji = -k equaling
. But also is ji = -k equaling  *
*  =
=  . Color multiplication in normal order
. Color multiplication in normal order  *
*  is the right one.
is the right one.
Likewise is -i * -j = k or  *
*  =
=  , while -j * -i = -k or
, while -j * -i = -k or  *
*  =
=  . Anticolor multiplication in normal order
. Anticolor multiplication in normal order  *
*  must be chosen there.
must be chosen there.
Let's apply this in Fig. 3.2 at page 3 of the storyline QCD.
START QUOTE
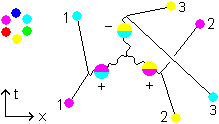 Fig. 3.2
Fig. 3.2
 *
*  = -k * -i = j (1)
= -k * -i = j (1)
 *
*  = -i * -k = -j (2)
= -i * -k = -j (2)
(1) and (2) superpose and cancel out,
(j) + (-j) = 0
In fig. 3.2 the shown outcome  = -j is only one of the two outcomes j and -j.
= -j is only one of the two outcomes j and -j.
STOP QUOTE
We judge -k * -i from (1) as color taken out of the normal order
as being right. And we see -i * -k from (2) as taken out of the reversed order
and thus not to be used here. The canceling out of (1) and (2) in fig. 3.2 would not be true then.
Next figure to apply this can be Fig. 3.3 at the same page.
START QUOTE
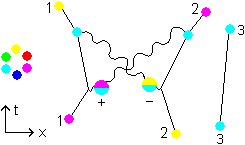 Fig. 3.3
Fig. 3.3
 *
*  = -k * j = i (3)
= -k * j = i (3)
 *
*  = j * -k = -i (4)
= j * -k = -i (4)
(3) and (4) superpose and cancel out,
(i) + (-i) = 0
STOP QUOTE
And here we meet a problem: where to take -k * j from, or j * -k? It is not found in a normal order, nor in a reversed order.This might mean we have to stop with this normal order vs reversed order business. It seems better to reformulate the starting theorem. The starting theorem was: red, green and blue applied together (and also cyan, magenta and yellow together) yields white, or 1 that is in quaternions. Instead would be better:
The color product end state of red, green and blue, and also the color product end state of cyan, magenta and yellow, equals +1 white or -1 black, both are colorless states (2.5)
We restore the quaternion canceling-out in fig. 3.2 at page 3 of the storyline QCD as well as the other quaternion canceling-outs and doublings-in-the-wavefunction at the page.
For 3 colors applied together (baryons) eq. (2.1) and (2.3) from this page superpose, yielding a color sum end state 1 -1 = 0. So the contribution in the wavefunction is zero. The baryon is colorless. (2.6)
For 3 anticolors applied together (antibaryons) eq. (2.2) and (2.4) superpose, yielding a color sum end state 1 -1 = 0 too, no contribution in the wavefunction either from this possibility. The antibaryon is colorless. (2.7)
So this yields another rule:
The color sum end state of red, green and blue, and also of cyan, magenta and yellow, equals zero (2.8)
Zero color can never be achieved by quaternion unit multiplication alone. Whatever multiplication order you take from no matter which quaternion units, their multiplication always yield a quaternion unit again. Zero is not a quaternion unit.
For baryons in first occasion the sum end state is i + j + k or -i -j -k. So for baryons, zero color sum end state can only be achieved by superposition of wavefunctions.
Let's generalize this to all color compositions:
The sum end state of a color composition (colors not merging) is always zero (2.9)
This is all not too different from electrostatics between e.g. an electron and a proton. Their electric charges sum up to zero, but when applied together in the law of Coulomb they multiply to -1 * 1 = -1, in this case, and not to zero.
Physical interpretation of multiplication order
We have met that reversing multiplication order is reversing time order. Let's generalize this. The order of multiplication is time order of multiplication.
The physical interpretation of multiplication order is: start multiplying with this, a little later with that and at last with this. (3.1)
As if it were couplings performed one after the other. Reversing time order is reversing multiplication order. ijk becomes different from jki and kij, despite that ijk = jki = kij. There are 3 times more possibilities to superpose. (3.2)
*i * j means first apply *i and then *j. Then *i *j (with outcome k) is different from *j *i (with outcome -k).
In the previous paragraph (2.1) up to (2.4) shows reversing multiplication order converts between end state +1 and -1. If multiplication order is time order of multiplication, then multiplication order can be different in frames of reference that differ a large speed. In one frame there is multiplied *i *j (outcome k), and in the other frame the same colors multiply *j *i (outcome -k). So different observers will see different outcome from the same coupling. We, Outside Observers, will never observe such a quark color reaction, so for us *i *j and *j *i will superpose. But in a baryon the *i *j can be observed by the third quark, while *j *i can be observed by a 4th quark, being part of a baryon, antibaryon or meson speeding by at near lightspeed. An energetic collision in a particle accelerator can cause this, the 4th quark near to the three others as well as the large relative speed of the 3rd and 4th quark. For gluons it's different. Gluons move at lightspeed and gluon worldlines are the same in all frames. Except the black gluon, if it has mass. (3.3)
Color conservation
Without mentioning explicitly so far, we used a kind of color conservation:
The color of a fundamental particle (quark, gluon) does not spontaneously change into another color (4.1)
An i cannot become j just like that, nor become -i. Colorless color +1 cannot change into a -1 just like that. To change the color of a quark or gluon one needs interaction with another color, a color coupling.
As to speak, A color on its own stays the same
- but colors are never alone. Only the colorless colors white +1 and black -1 can. Nevertheless we stick to this rule.
Another rule is that color is hidden
. We generalize (2.5) to:
The observed color product end state always is +1 or -1 (4.2)
This holds for baryons, antibaryons and mesons. It holds too for glueballs but not for gluNons from which the gluon is one of them.
(4.2) is a conservation law of colorlessness.
Mesons
And now for the mesons, two quarks together. A multiplication of two different colors like i and j always yield a colored thing, in this case a product end state +k or -k. Reversing multiplication order renders no effect. So different kind of colors are not permitted for the quarks in the meson. Two equal colors multiplication, whatever their sign, always yields +1 or -1.
i * i
j * j
k * k
= -1
= -1
= -1
-i * -i
-j * -j
-k * -k
= -1
= -1
= -1
i * -i
j * -j
k * -k
= +1
= +1
= +1
-i * i
-j * j
-k * k
= +1
= +1
= +1 (5.1)
We have a rule:
Quarks have color and antiquarks have anticolor *) (5.2)
This rule emerges when you state that there exists only quarks with color and that there is time reversal. Time reversal of the quarks with color i, j, k, 1 then yield the antiquarks with anticolor -i, -j, -k, -1. But what if we take this rule as a starting state only, after which things can change? At page 3 of QG this is called the Minus Sign Go Wild approach.
If the meson starts out as a color and an anticolor, then color conservation (4.1) ensures that there is no way to change only one of the colors into its opposite, yielding two colors or two anticolors in the meson. So the first two columns of table (5.1) with their dangerous product end states of -1, don't apply.
In accepted QCD two quarks of same color together, or two antiquarks of same anticolor together, are by no means colorless. One such a quark isn't colorless, so two of them together (without merging) certainly is not either. (5.3)
The multiplication of two identical colors however is colorless:
i * i = j * j = k * k = -i * -i = -j * -j = -k * -k = -1
In Minus Sign Go Wild
this means these composites are allowed in forming a meson - which is not allowed according to (5.2). I conclude (4.2) alone is not sufficient for judging allowance and Minus Sign Go Wild is judged false. Let's adopt (5.2) as a condition too, next to (4.2). As a consequence quarks-with-anticolor and antiquarks-with-color as intermediate states are not allowed, although in many cases it is very tempting to allow it.
Maybe (5.2) is even too restrictive. Application 4 at page 7 of QQD shows how black glueball exchange can turn a baryon (e.g. uud) with three colors in a baryon (still uud) with three anticolors, and back again. Likewise an antibaryon like uud (underlining means anti- ) with anticolors could turn into the same antibaryon uud with colors, and back again. Apart from (5.2) there seem to be no objection to this.
i * -i, j * -j and k * -k from the 3rd column would superpose swiftly by absorption from the Higgs field (the meson consists of quarks that absorb mass from the Higgs field), a reasoning that is ahead of chapter 4, see paragraph The Quaternion Approach at page 3 of QG...
i * -i
i * 1 * -i
= i * -k * k * -i
which can be interpreted as the quark pair i -i absorbing one vacuum particle, the gluon pair ( -k k ). Then the -k and k separate from each other.
= i * -k * -i * -k
which can be interpreted as the quark i that emits the gluon -k and the other quark -i that absorbs the gluon -k (the quark is always right multiplied by the gluon)
= j * -j
Nowadays insights indicate this is the Higgs mechanism for the 3rd generation: quarks b and t, the tauon and the tau-neutrinos. If you are reading TONE you better take this for granted and re-read it later, after you have red chapter 42.
And likewise for the members of the 4th column of table (5.1).
Then i * -i and -i * i from the first row of the 3rd and 4th column respectively in table (5.1), superpose by black glueball exchange, see Still application 4: Mesons the upper row, at page 7 of this storyline. This is more slowly because of the mass of the black glueball. Likewise for j * -j and k * -k. This violates (5.2), you now have a quark with anticolor and an antiquark with color, although it still keeps the color state at +1 or -1. (5.4)
The net color sum end state of the meson is zero:
+i -i = +j -j = +k -k = -i +i = -j +j = -k +k = 0. (5.5)
The reasoning of the black glueball as candidate of Dark Matter (the extra matter that keeps the too-fast stars within our Galaxy) uses (5.2) as key argument, see text just below Fig. 3.9 at page 3 of QCD and see The only clue for Dark Matter (...) in the column at the right at page 2 of THE EXPANSION OF THE UNIVERSE. (5.6)
Also the reasoning that the positron is the particle and the electron is the antiparticle uses (5.2) as key argument, see Electrons as Baryons at page 4 pg QG. (5.7)
So for the sake of these two advantages we decline from Minus Sign Go Wild.
In Minus Sign Go Wild baryons as well as antibaryons have their quarks at colors i and j and k, with minus or plus signs in front of them arbitrarily. Mesons then have color i i, or j j, or k k, with minus or plus signs in front of them arbitrarily.
Minus Sign Go Wild stays so close to the original quaternion definition,
i = j
= j = k
= k = ijk = -1
= ijk = -1
where ijk = -1 is for baryon and antibaryon colors and i = j
= j = k
= k = -1 are for the meson's colors. (5.8)
= -1 are for the meson's colors. (5.8)
*) According to the paragraph Everything can couple to everything by color force at page 5 of QG, the electron would be able to absorb a black glueball, a glueball of color -1. When it does so, the color of the electron changes from -1 into +1, see (1.2) and (1.3) in paragraph Electrons as Baryons at page 4 of QG. The changed electron will now readily be abs orbed by any quark in the nucleus of the atom, compare item 3) in the same paragraph. To prevent this and in doing so saving our electrons and our one and only Dark Matter candidate, I would propose to extend (5.2) above in this paragraph to all particles that come in particles and antiparticles.
Particles have color and antiparticles have anticolor (5.9)
This is in line with (5.5) and (5.6) in The color of the neutrino at page 4 of QG. Our black glueball now has no way to be absorbed by any matter particle and is bound to roam about for ever.
But this runs ahead of pages to come in the TONE storyline.
IF YOU ARE READING TONE FOR THE FIRST TIME, ALL NECESSARY THINGS FOR THE CHAPTERS TO COME ARE GIVEN NOW, YOU CAN SKIP THE REST OF THE PAGE AND READ IT LATER.
Some worked out color reactions
The following examples are illustrative for how colors work.
1)
i * i
= i * -k * k * i
The appearance of -k k can be the absorption of a vacuum particle as presented in The quaternion approach of the Higgs mechanism at page 3 of the QUATERNION GRAVITATION storyline.
= i * -k * i * -k
and this last line represents a quark i that emits a gluon -k and the other quark i that absorbs the gluon -k (the quark is always right multiplied by the gluon)
= j * j
So i i can spontaneously change into j j. Likewise i i can change into k k.
i i = j j = k k superpose. (6.1)
However, in a single hadron there are never two i's, i * i never occurs within a single proton or neutron. i * i can appear between neighboring nucleons, or when a meson passes by a nucleon very near to it, see (1.7). But i * i that becomes j * j as just described will leave the nucleons and/or the meson wherein this is happening both in a colored end state, which is forbidden. We conclude i * i doesn't occur and (6.1) and (6.4) plays no role in hadrons or between hadrons. (6.2)
i * i
= i * -1 * -1 * i
= i * -1 * i * -1
-i * -i
So i i can change into -i -i by black glueball exchange, and likewise j j into -j -j and k k into -k -k. (6.3)
If not the demand of colorless end state will forbid it, two colors in composition would continuously change into their opposite colors and back again by black glueball exchange. In the baryon this has a peculiar result, see application 4 at page 7 of this storyline. In the meson it causes a net color sum end state of zero: +i -i = 0.
From (6.1) and (6.3) follows:
i i = j j = k k = -i -i = -j -j = -k -k superpose. (6.4)
The black glueball has mass, according to (2.2) in paragraph Building vacuum from gluons at page 2 of QG. The transition between i i and j j and k k and also the transition between -i -i and -j -j and -k -k goes relative fast, see the The quaternion approach of the Higgs field at page 3 of QG (QUATERNION GRAVITATION), while the transitions between i i and -i -i, and likewise between j j and -j -j and between k k and -k -k, goes relative slow, because of the mass of the -1 color. When you start e.g. with i i then the other states from (6.4) do superpose immediately, but not immediately with same amplitude.
3)
i * j
Start state present in baryons only; k color not shown.
= i * -k * k * j
= i * -k * j * -k
This is quark i that emits a gluon -k and quark j that absorbs the gluon -k.
= j * -i
or, when the emerging pair is k -k, leading to end state
= -j * i
So i and j can swap color but one of the colors changes sign.
We met such a sign change before, see (1.4), (1.5) and (1.6) at the previous page. But there it was half a gluon exchange that makes sign change. While here it is no gluon exchange at all but a vacuum marble absorption, a Higgs absorption, replacing the gluon exchange. This is worked out in the The quaternion approach at page 3 of (QG). (6.5)
Is it possible to regard every computation act as a particle reaction? i * -k * k * j changes into i * -k * j * -k by quaternion computation rule; ij = -ji by computation rule. But it can also be seen as a physical swap of colors with a minus sign appearing.
The swapping reaction then is part of the description of the swapping reaction. It is an endless series of disturbances we recognize from renormalization techniques. But in renormalization normally there is a main reaction and added to it are the disturbances. However in this case, as far as I can see, the main reaction doesn't exist, only the series of disturbance does.
One better uses the quantum view of superpositions: ( i * j ) and ( i * -k * k * j ) and ( i * -k * j * -k ) and ( j * -i ) and ( -j * i ) are states of same outcome and thus superpose. One of the possibilities will be chosen according to chances of occurrence (square of amplitude). No one bothers about how one possibility mechanically goes into the other. (6.6)
But then again, do these states superpose simultaneously? Does it take time to go from state ( i * j ) to state ( i * -k * k * j ), does the emergence of the vacuum particle take at least one typical reaction time (10^-23 s)?
Subsequently
j * -i = j * k * -k * -i = j * k * -i * k = i * j
and
-j * i = -j * -k * k * i = -j * -k * i * -k = i * j
return to the starting state i j.
Three gluons applied together
In a baryon there are the colors i, j and k together, or -i, -j and -k in the antibaryon, and that's all there is to the colors in a groudstate baryon.
However, I conjecture that gluons can form composites, gluons that glue together into a particle-like object without directly merging. It are color compositions that are formed then. A single gluon can be colored and so can be the composite.
Call a composite of 3 gluons a glu3on, pronounce glue-three-on. A gluon then is in fact a glu1on, a glue-one-on. When the color product of the composing three gluons is +1 or -1 we call it a glue3ball.
The 3 gluons can merge to 1 gluon relatively easy, see paragraph Can 3 gluons change into 1 gluon easily? at page 7 of QCD. When they don't merge and stay a glu3on then the three gluons are expected to stay at a certain distance relative to each other, because at zero distance the force between colors is zero and the force is proportional to the distance, see paragraph The proton at page 4 in the storyline QCD.
When the colors of a glu3on have the letters i, j and k, regardless the sign in front or the order of multiplication, then the multiplication outcome will always be a real state +1 or -1.
If not i, j and k then there always is a pair i i or j j or k k (regardless their sign in front). Therefore according to the rules from previous paragraph, are superposing:
i i i, j j i and k k i;
i i j, j j j and k k j;
i i k, j j k and k k k;
i j k, -i -j k, -i j -k and i -j -k;
-i -i -i, -j -j -i and -k -k -i;
-i -i -j, -j -j -j and -k -k -j;
-i -i -k, -j -j -k and -k -k -k;
-i -j -k, i j -k, i -j k and -i j k; (7.1)
8 different three-color compositions that cannot transform into one another by gluon exchange within the glu3on and thus do not superpose. They have to be set initially.
The color product end state of these compositions are:
i i i = j j i = k k i = -i
i i j = j j j = k k j = -j
i i k = j j k = k k k = -k
i j k = -i -j k = -i j -k = i -j -k = -1
-i -i -i = -j -j -i = -k -k -i = i
-i -i -j = -j -j -j = -k -k -j = j
-i -i -k = -j -j -k = -k -k -k = k
-i -j -k = i j -k = i -j k = -i j k = +1 (7.2)
These end states are the colors of the 8 gluons. The compositions are the possible glu3ons that superpose with the gluons, regardless their multiplication order.
Regard color composition i i j.
i * i * j = j * i * i = -j and i * j * i = j. In 2/3 of the cases the outcome is -j and in 1/3 the outcome is j. Superposing yields
2/3 * -j - 1/3 * j = 1/3 * -j (7.3)
But, as said in (3.2), i * i, j * j and k * k don't occur in hadrons because they leave a colored end state.
In (5.1) in Pauli matrices and the color -1 of the Higgs mechanism at page 3 of QG is suggested that glu3ons are massive. A particle has mass OR it is massless, even the tiniest mass value will do. The glu3on mass would spoil the superposition with the massless gluons. When energy for the glu3on mass is lacking, gluons will be massless, except for -1. As soon as energy is available, the massless glu1on plus the energy concentrated in its parcel of spacetime, superposes with the massive glu3on state. It does so for only one instant. After that single moment the massless glu1on state and the massive glu3on state depart from each other. Because of its mass, the glu3on will have range. But gluons already have range. (7.4)
Consider gluons i, j and k in one glu3on. Since kji = +1 and ijk = -1 (both are colorless) it's a glue3ball, a colorless gluon.
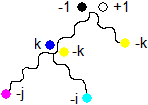
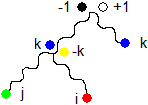
![]()

The k and -k colors shown next to each other in the picture do not represent two different particles but only one particle in two superposing states. Likewise the black and the white colors. From +1 or -1 there is a like chance to convert back to ANY glu3on state. These are only two of them.
A previous attempt
The application of colors goes by means of gluons, there is no other way. All gluons have 2 colors, so e.g
*  *
*  *
*  = * (
= * (  /
/  )
*
)
*  =
=  *
* 
and for the single blue we have no gluon to transmit it.
(Mind green divided by cyan equals green left-multiplied by anti-cyan, red that is.)
Applying the 3 colors twice then can be done by 3 gluons:
ijkijk = *  *
*  *
*  *
*  *
*  *
* 
= * (  /
/  )
* (
)
* (  /
/  )
* (
)
* (  /
/  )
)
=  *
*
 *
*
 = j/-i * i/-k * k/-j
= j/-i * i/-k * k/-j
= kji = *  *
*  *
*  = 1
= 1
use the gluon table.
We anyway have ijkijk = kji, which here means applying the colors twice equals applying the colors in reversed order once
.
So a rule like reversed multiplication order for colors and normal order for anticolors
might be replaced by the rule apply this or that twice
. The appliance of the 3 colors twice, or the 3 anticolors twice, then always gives -1 * -1 = 1 * 1 = 1
Applying all colors (the 3 colors applied once and the 3 anticolors applied once). When applying (2.2) and (2.3) the outcome is 1:
*  *
*  *
*  *
*  *
*  *
*  = k * j * i * -i * -j * -k = 1
= k * j * i * -i * -j * -k = 1
Contrary, walking around the colorcircle
, no matter what direction or starting point, always yield -1.
*  *
*  *
*  *
*  *
*  *
*  = k * -i * j * -k * i * -j = -j * -i * -k = -1. Then walking around the colorcircle twice always yields -1 * -1 = 1.
= k * -i * j * -k * i * -j = -j * -i * -k = -1. Then walking around the colorcircle twice always yields -1 * -1 = 1.
Any color multiplication sequence ends up with one out of 1, i, j, k, -1, -i, -j, -k.
i = j
= j = k
= k = (-i)
= (-i) = (-j)
= (-j) = (-k)
= (-k) = -1
= -1
-1 * -1 = 1 * 1 = 1
So any factor sequence of colors, when repeated 4 times at most, will always yield 1, the colorless white end state.
Open color is never observed. All color reactions are virtual. When a quark emits a gluon, it sets out as the superposition of the 8 possible colors, 1, i, j, k, -1, -i, -j, -k. Whatever color exchange might have taken place, after 4 times setting out as the same superposition of the 8 possible colors, each exchange occurred 4 times. Yielding net color white. So it seems IF colors are virtual, THEN they practically are confined. Is this all there is to color confinement?