Four quarks in the shell



Read the book of Feynman, QED - The strange theory of light and matter. And Scientific American of June 1980, Gerard 't Hooft, Gauge theories of the forces between elementary particles. In Four quarks in the shell knowledge of renormalization theory is necessary at that level.

A little knowledge about quaternions is necessary. The quaternion approach of strong force colors is worked out in the storyline QQD.


Four quarks in the shell

Let's go back to the superposition of innumerable quark-antiquark pairs, shielding the naked color of the quark. The color coupling constant is about 1. Therefore 4 quarks appearing in 2 quark antiquark pairs, all within their time borders, all seeing each other, count with same importance as 2 quark antiquark pairs superposed to each other at same mutual distance. (The superposed two quark pairs don't see each other, don't react with each other.)              (a)

We just suppose the 4 quarks to appear within their time borders, at the Earth surface within 10^-19 m or 10^-4 fm (see EXPANSION OF THE UNIVERSE, page 2, paragraph The calculation of the time border). We assume the two pairs to emerge simultaneous within a length of time of 10^-23 sec. Quarks have maximum attraction at about 0.9 fm, so the 4 quarks hardly attract each other. They don't form pairs under strong force attraction. And they can't separate much more since then they don't coincide enough anymore to gain masslessness.

Emerging pairs always consist of a quark and an antiquark with opposite taste, color and spin. Electric charge already is in the taste, e.g. when the taste is u then electric charge is +2/3 times the electron charge. When the taste is d then the electric charge is -1/3. When the tastes are opposite, the electric charges are so too.

Impulses don't have to be opposite. If one quark from the pair has a small impulse and the other quark has a large impulse in a different direction, when massless coinciding the impulse sum determines the direction and the energy of the resulting lightspeed gluon. It is the direction of the frame of reference in which the quarks do have opposite impulse.

A and D are quarks, B and C are antiquarks (the underlining means it is an antiquark), AB is one emerging pair, CD is the other emerging pair, = spin +1/2, = spin -1/2. The colors of the pairs can be or or . Let's suppose the two emerging quark pairs have different color.

A       C
B       D       (5.1)
A       C
B       D       (5.2)

 
The double pair in (5.1), and in (5.2) as well, form 2 gluons which can be investigated along 3 ways: AB CD, AD BC and AC BD (denoted as II column pairs, X crosswise pairs and = row pairs).

A and B have opposite spin and so do C and D.

II pairs in (5.1) and (5.2): quark spins +1/2 -1/2 = 0, the double pair can form two colorless spin 0 gluons. White gluons don't glue.           (b)

X pairs in (5.1) and (5.2): the pairs are a particle-particle pair and an antiparticle-antiparticle pair, wherein massless coinciding is not possible. So X-pairs will not form gluons in (5.1) and (5.2):.

= pairs in (5.1): the 4 quarks can form two colored spin 1 gluons, quark spins +1/2 +1/2 = +1 and -1/2 -1/2 = -1.              (c)

In fact, as will be described below, in 18 from 25 cases the two spin 1 gluons in = have color and in 7 cases they are white-white or black-black.

= pairs in (5.2): two colored spin 0 gluons can be formed, the gluons that make up the vacuum, see page 2 of QG.              (c)

(So the vacuum can be made of spin 0 gluons directly. But when the gluons have color these colors have to be canceled. One still needs gluon pairs.)

Four quarks making up 2 gluons is the smallest number of quarks to appear within their time borders, in order to form colored spin 1 gluons.

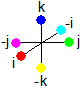
Let's regard the colors a little better. Let's go into quaternions. Eventually use the gluon table. Regard the 2 pairs again. Each pair consists of a color and an anticolor. For each pair that emerges, there are 4 possibilities: and and . And the fourth pair, is it ? The result per pair is to be taken as the application of both colors one after the other. One has to multiply the colors with each other and in quaternions multiplication order makes a difference. So which order is to be taken? Set e.g.:

A     C    
B =      and D =           (5.3)

 
II pairs:           (5.4)

= i * -i = = j * -j = 1 = , so the II-pairs form a white gluons. Multiplication order is not important. But how for the other combinations?

 
= pairs and X pairs:           (5.5)

= -j * i = k =
= i * -j = -k =
 

= j * -i = k =
= -i * j = -k =
 

= i * j = k =
= j * i = -k =
 

= -i * -j = k =
= -j * -i = -k =
 

We didn't need to worry. It are all combinations of i and j - with or without a minus sign in front - and the multiplication always will yield k, one with a minus sign in front and the other without. All possible arrangements and orders of the quarks of color i and j (with or without a minus sign in front) yield the gluon pair k -k. Two different pairs of color-anticolor that appear, always yield the third possible color-anticolor pair.

Quarks have color and antiquarks have anticolor           (5.6)

see (3.41) in paragraph mesons at page 3 of QQD, a result that should not be forgotten.

The X pairs (3rd and 4th scheme, with i * j and -i * -j respectively) are particle-particle pairs or antiparticle-antiparticle pairs, in which massless coinciding is not possible. The X pairs don't yield gluons.           (5.8)

The only possibility to form colored gluons are the = pairs. It then can be spin 1 colored gluons or spin 0 colored gluons, depending on whether the spin distribution is like (5.1) or (5.2).           (5.9)

What if the two pairs of quarks are the same?

A     C    
B =      and D =  

= i * -i = 1 =
= -i * i = 1 =
 

= i * i = -1 =
= -i * -i = -1 =
 

          (5.10)

The = pairs as well as the II pairs yield white gluons (first scheme).           (5.11)

The X pairs (last scheme, with i * i and -i * -i) would yield black gluons only. However, it are a particle-particle pair and an antiparticle-antiparticle pair respectively, in which massless coinciding is not possible. The outcome of black gluons is not possible here.           (5.12)

So when AB and CD is the same pair of colors the result always is a pair of white gluons.           (5.13)

The particle and antiparticle in a pair that emerges in the shell cancel each other out, that's why they can appear. When do colors cancel each other? + = + = + = + = i -i = j -j = k -k = 1 -1= 0, the colors and anticolors happen to add up to zero. But in quaternions, when we apply colors, we don't add them, we multiply them. Then * = * = * = i * -i = j * -j = k * -k = 1 and indeed 1 is the neutral element with respect to multiplication.

But black and white multiply to * = * = 1 * -1 = -1 * 1 = -1. How does this work? White and black are opposite colors, is the particle and is the antiparticle, they cancel each other out. So they can emerge as a particle-antiparticle pair.

With two such pairs of quarks it would do: * * * = -1 * -1 = 1. And subsequently the four quarks, all within their time borders and within the same 10^-23 sec, rearrange as two quark pairs and . These two pairs are gluons. But if the colors in them would be applied, one after the other merging with a target color, a target quark, they would act as a black gluon, a gluon with color -1. And that is too dangerous! It would change the color of the target quark to its opposite, leaving the baryon or meson it is in in a colored end state. And that is forbidden.

That is to say, in a baryon it is forbidden. And too when one of the pairs only couples to one of the quarks in the meson. But if the two pairs emerge and depart from each other and one of them merge with a quark of a meson and the other merging with the other quark, then the color of both quarks of the meson change into its anticolor. But then you have quarks with anticolor, or antiquarks with color, which is forbidden too, see (5.6).

So they will escape. Since they have no color they are allowed to stay on their own.

The quark composition of the white gluon is or or       (5.14)

But I cannot conclude otherwise than

The quark composition of the black gluon is       (5.15)

White and black gluons might be their opposite, they really differ a lot from each other!

In paragraph Filling in the vacuum marbles at page 2 of QG is suggested the black gluon has mass. If so, then a quark combination certainly will emerge at much lower pace than the massless colored gluons with their imaginary quaternion units.

At page 4 of QG black and white quarks are recognized as the electron and the positron respectively. The e- and e+ have mass of 0.511 MeV and the masses of the quarks are thought to be quite different from that. When they form gluons the absorption of mass from the Higgs field by the particle equals the emission of the Higgs field by the antiparticle. It makes no difference how large those masses are as long as they have equal magnitude. So I don't think the masses on itself make a difference. The e- as well as the e+ have 1 unit electric charge, while the quarks A, B, C and D have fractional electric charges. The electic charges that form the gluon have equal but opposite magnitude and cancel each other out. So I don't think the electric charges make any difference too in the gluon composite. When apart, somehow the ECR (electric charge redistribution) provides the former quark with integer electric charges, instead of the quarks original fractional electric charges.

A few other reactions:

A     C    
B =    and D =  

= i * -1 = -i =
= -i * 1 = -i =
 

= j * -1 = -j =
= -j * 1 = -j =
 

= k * -1 = -k =
= -k * 1 = -k =
 

X pairs form no gluons, II pairs form a white gluon and a black gluon. It are the = pairs that are interesting.

= 1 * 1 = 1 =
= 1 * 1 = 1 =
 
= 1 * -1 = -1 =
= 1 * -1 = -1 =
 
= -1 * -1 = 1 =
= -1 * -1 = 1 =
 

As you see, the pair as outcome (one above the other) doesn't occur.

It's all multiplication of colors. That means coupling, merging of the preceding two colors into a merger color, see (3.02) and (3.03) at page 3 of QQD. From the merger color the information is lost what precisely were the colors of the quarks just before merging.

However, how nice would it be when the two quarks that constitute the gluon, would stay apart, just like the e- and e+ do in the photon, see page 4 of NET FORCE IN QED. For the process of massless coinciding it is necessary the quark absorbs from the Higgs field the same amount as the antiquark emits to the Higgs field, and that supposes the quark and the antiquark to exist as separate entities. The gluon then resembles more the old gluon from accepted QCD with its upper and lower color, like , and . When the gluon is emitted by a quark 1, follows its short route and is absorbed by another quark 2 nearby, the quark-antiquark pair that makes up the gluon is taken from the shell of the emitting quark 1 (without merging), follows its route without merging and then takes its place between the infinite other quark-antiquark pairs in the shell of quark 2, all without ever having merged.

So it is as if the colors of the quarks in a gluon merge while the other properties of the quarks, the quarks themselves as to speak, do not! Can that be?

And last but not least there is taste. In the 1st generation there are two tastes available for quarks: u and d. There u has always +2/3 electron charge, d has always -1/3, anti-u = u has -2/3 and anti-d = d has +1/3 electric charge. As to speak, electric charge is in the taste. There are 4 possible u and d distributions for the quark pairs AB and CD that emerge in the shell. Keep in mind we assigned spin +1/2 to A and C, and spin -1/2 to B and D.

A C   u u   d d   u d   d u  
B D   u u   d d   u d   d u              (d)

In the first, and similar in the second pair of pairs, II-pairs as well as = are possible, there the tastes cancel out. But X would form charged gluons and that are no gluons. Moreover, X are particle-particle pairs or antiparticle-antiparticle pairs, in which massless coinciding is not possible.              (e)

In the third and fourth pair of pairs, the 3rd and 4th scheme in (d), situation is even worse: only II can form gluons (colorless spin 0 gluons only) and X and = would yield charged gluons.

The = pairs in the 1st and 2nd scheme are the only possibility to form colored spin 1 gluons, the gluons that mediate the strong force.

Mark the = pairs in the 3rd and 4th scheme are interesting: they form pairs of spin 1 particles of unit charge and the particles can have color but may be white or black too. IF u and d have different mass - and I think they have - THEN the Higgs field absorption of the one do not cancel the Higgs field emission of the other precisely. The quarks cannot coincide massless, the particle will have some remnant mass. The quarks are within their time borders; they will not separate because the presence within the time border gives some mass reduction. Separation means the quarks have to be supplied by their complete mass; that thus might be huge. We know little about the quark mass, see paragraph Quark mass at the previous page. Admit, the particle has some resemblance to the W+ W- particle. But well, why W has mass 80385 MeV while the meson consisting of the same quarks then, has mass 140 MeV?

For the photon we assumed it consists of an electron and a positron massless coinciding, and the electron and positron then are assumed to be a quark of color -1 and +1 respectively. In accepted QCD the coupling constant of W+ W- and the coupling constant of the photon are nearly the same. This means that the u d and d u pairs that constitute W+ W- must be quarks that don't glue: u- and d-quarks of color white and u- and d-antiquarks of color black. Maybe an electric charge redistribution will take place. It couples by the strong force (but doesn't glue). It interacts by the electromagnetic force. The W+ W- reacts as a kind of massive photon. This then is the W+ and W-.

When the u d and d u pairs have color, then it is the meson, as also is assumed in accepted QCD. The quarks in the meson have opposite colors, i -i or j -j or k -k. A meson can spontaneously convert to W+ W- or Z0, and vice versa. Which means that the particle pairs i -i, j -j, k -k and the particle pair 1 -1 in principle can convert into each other. The quark pairs i -i, j -j, k -k are massless in the sense that mass absorption cancels mass emission. In 1 -1 the -1 maybe has mass, see (2.7) and further below in Building vacuum from gluons at page 2 of QG.

We now conclude the reasoning of four quarks in the shell leading to real gluon pairs with color (as well as white or black gluon pairs). Finally one of the colored spin 1 gluons formed from the 4 quarks in the shell, can be absorbed by the real quark in which shield all this is happening, changing its real color. The other color then can be reabsorbed too (yielding no change at all) OR escape to another real quark. This can happen in mesons as well as in baryons.

Also possible is that both gluons leave the real quark where they are born, each of them going to a different quark - in baryons only, baryons have 3 quarks. The mother quark then doesn't change color, but the other two do.

Gluons might be CTL's (Closed Time Loops), see CTL considerations at page 8 of SR.


And now for the chances

(   tO rEVISE   )

The 4 quarks in the shell emerge in 2 particle-antiparticle pairs AB and CD. From (a) there is a chance of 1 out of 2 for emerging 4 quarks all seeing each other within their time borders.              (chance 1 = 1/2)

The remaining chance of 1 out of 2 is for the emerging pairs just to superpose, despite they appear at precisely the same spots.              (chance 2 = 1/2)

A C   u u   d d   u d   d u  
B D   u u   d d   u d   d u              (d)

 
The best way to proceed now is to start with the taste. We are in chance 1. When written down as in (d) there is a chance of 1 out of 2 for the first or second pair-of-pairs to form.              (chance 3 = 1/2)

The remaining chance of 1 out of 2 is for the third or fourth pair-of-pairs to be formed, yielding colorless spin 0 gluon pairs only.              (chance 4 = 1/2)

(For convenience we assumed the u is as likely to appear as d, which might be wrong)

When in chance 3 (1st and 2nd pair-of-pairs in d), there is a chance of 1 out of 2 for II-pairs, yielding sole colorless spin 0 gluons.              (chance 5 = 1/2)

And a chance of 1 out of 2 for = pairs to be formed.              (chance 6 = 1/2)

And no chance for X-pairs to be formed.

We now shift to spin and color. Set A at spin +1/2 and B at spin -1/2. When in chance 6, there is a chance of 1 out of 2 for C spin +1/2 and D spin -1/2.              (chance 7 = 1/2)

And a chance of 1 out of 2 for C spin -1/2 and D spin +1/2.              (chance 8 = 1/2)

As long as we have no reason to assume otherwise, we assign an equal chance to the 5 possible color-anticolor pairs to emerge. In the scheme at the right we see 25 possible combinations, 18 have color and glue, and 7 are white-white or black-black pairs from which the gluons don't glue.

18/7 = 2.57, 7/18 = 0.39, 25/18 = 1.39, 18/25 = 0.72, 25/7 = 3.57, 7/25 = 0.28.

In chance 7 there is a chance of 18 out of 25 for a pair of colored spin 1 gluons, the particles that make up the strong force.              (chance 9 = 18/25)

When in chance 8, there is a chance of 7 out of 25 for a pair of colorless spin 1 gluons (black-black or white-white).              (chance 10 = 7/25)

When 4 quarks in 2 pairs emerge within their time borders, the chance for two colored spin 1 gluons (two opposite colored spin 1 gluons) is:

Chance 1 x chance 3 x chance 6 x chance 7 x chance 9

= 1/2 * 1/2 * 1/2 * 1/2 * 18/25 = 18/400 = 0.045 or about 5 percent.

This percentage is making up the entire strong force. For spin 1 colored gluons, what we interpreted so far as one reaction in one cycle of time, up until now taken as 10^-23 s, must be about 1/0.045 = 22 reactions, 22 cycles of time - from which only one of them is yielding colored spin 1 gluons. One strong force cycle of time then must be rather 0.5 * 10^-24 s. In that time a light speed gluon covers only 0.15 fm.


References

Scientific American june 1980, Gerard 't Hooft, Gauge theories of the forces between elementary particles, for the model used in Four quarks in the shell.