Let's return to equation
Q(A 
B) * g * Q(B C) * GL(B D) (2.1)
(left part)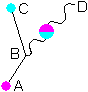 
(right part) 
The left part of the picture depicts eq. (2.1), but now it specifies the gluon is emitted by the quark. The right part of the picture depicts an absorption of the gluon by a quark.
-j = -i * (i * -j) (2.2)
When (left part of the picture) -j is the starting state (quark with color -j) and -i * (i * -j) is the end state (quark of color -i and gluon -j / -i = i * -j), then eq. (2.1) is an emission.
When -j is the end state and -i * (i * -j) is the start state (right part of the picture, the gluon meets a second quark now), then eq. (2.1) describes an absorption.
Mark we RIGHT MULTIPLY the quark Q by the gluon GL: Q * GL
Otherwise eq. (2.2) doesn't work. (2.3)
An application of this is e.g. at item 6b at page 1 of FORWARD BACKWARD TIME DIRECTION.
Let's provide every action with its color.
-j * Q(A B) Quark Q going from place A to place B
g coupling constant
-i * Q(B C) Quark Q going from place B to place C
Gluon GL -j / -i * GL(B D) (2.4)
When every action is provided with its colors and taking into account the mentioned right multiplication, then equation (2.1) describing the left part of the picture, becomes:
-j * Q(A B) * -i * Q(B C) * -j / -i * GL(B D) * g
= ( -j ) * ( -i ) * ( i * -j ) * Q(A B) * Q(B C) * GL(B D) * g
= - Q(A B) * Q(B C) * GL(B D) * g
(2.5)
It's a pity, the equation changed sign! Let's try to put the factor -j * Q(A B) at the end, instead of in front:
-i * Q(B C) * -j / -i * GL(B D) * g * -j * Q(A B)
= ( -i ) * ( i * -j ) * ( -j ) * Q(B C) * GL(B D) * g * Q(A B)
= - Q(B C) * GL(B D) * g * Q(A B) (2.6)
which is the same outcome. The reversal doesn't help.
Other orders are not allowed. From eq. (2.2) follows we have to keep the -j / -i after the -i. Therefore there is no other way: the colors in the process described so far give outcome -1 in front of the wavefunction contribution. This doesn't leave things unchanged. It will lead to a different outcome in renormalization.
Observations show no color, we never see a bare gluon. The range of color is about 1 fm (= 10^-15 m). The gluon is absorbed within this timeframe, by a quark or other gluon. The gluon only reacts with quarks or other gluons (until told otherwise), so the gluon is not observed in between. Therefore the left part of the picture is always accompanied by the right part.
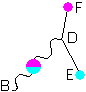
Q(E D) * GL(B D) * g * Q(D F) (2.7)
Eq. (2.7) is the equivalent of eq. (2.1). When provided with colors eq. (2.5) becomes:
( -i ) * Q(E D) * ( -j / -i ) * GL(B D) * g * ( -j ) * Q(D F)
= ( -i ) * ( i * -j ) * ( -j ) * Q(E D) * GL(B D) * g * Q(D F)
= - Q(E D) * GL(B D) * g * Q(D F) (2.8)
Which follows precisely the calculation that leads to eq. (2.5), also with outcome -1 in front of the wavefunction contribution.
The emission and absorption together is again one single diagram:
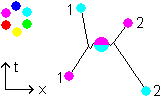
The equation of this diagram should be the multiplication of eq. (2.5) times eq. (2.8). The minus signs of (2.5) and (2.8) would cancel each other. The quaternion unit parts
( -i ) * ( i * -j ) * ( -j ) from (2.6) and
( -i ) * ( i * -j ) * ( -j ) from (2.8) are precisely the same. As you can see, when we would write out (2.5) times (2.8), the factor -j / -i * GL(B D) would appear twice. However, the gluon goes from B tot D once. If we would skip one of the gluon factors -j / -i * GL(B D), then also one factor -j / -i = i * -j = -k would be missing and the end result would have a color.
We can skip one of the factors GL(B D) and assign -j / -i to the coupling g instead of to the factor GL(B D).
There always are two couplings assigned to the gluon, one for emission and one for absorption - color is never observed so there has to be. The provision of every action with its color then becomes:
Quark Q going from place A to place B -j * Q(A B)
coupling of gluon GL ( -j / -i ) * g
Quark Q going from place B to place C -i * Q(B C)
Gluon GL going from place B to place D GL(B D) (2.9)
In a reaction equation involving emission and absorption of a gluon of color k (take the color to be k) the k has to be assigned to the coupling, in fact one k at both ends of the gluon (2.10)
Cycles of colors and quaternion units
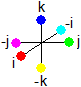
Quaternions are cyclic, that is, the multiplication of the imaginary quaternion units show a 3-step cycle.
Funny but not essential
| i | * | j | = | k | ||||||
| j | * | k | = | i | ||||||
| k | * | i | = | j | ||||||
| i | * | j | = | k (2.20) |
| * | 
| = | 
| ||||||
|
| * |
| = |
| ||||||
|
| * |
| = |
| ||||||
|
| * |
| = |
|
Step 4 equals step 1.
Reversing multiplication order gives
| j | * | i | = | -k | ||||
| k | * | j | = | -i | ||||
| i | * | k | = | -j (2.21) |
|
| * |
| = | 
| ||||||
|
| * |
| = | 
| ||||||
|
| * |
| = | 
|
This is not very cyclic.
Sign multiplication is cyclic too, like quaternions. Here - * - = +
means e.g. -1 times -1 = +1
.
| - | * | - | = | + | ||||||
| - | * | + | = | - | ||||||
| + | * | - | = | - | ||||||
| - | * | - | = | + (2.22) |
and so on. It is a 3-step cycle like (2.10), the 4th step equals step 1.
+ * + is cyclic too, but it is a little boring:
| + | * | + | = | + | ||||||
| + | * | + | = | + | ||||||
| + | * | + | = | + | ||||||
| + | * | + | = | + (2.23) |
and so on.
When mapping (2.20) and (2.22) onto each other, you see the multiplication of the negative imaginary quaternion units (the anticolors -i, -j and -k) show a kind of 3-step cycle too.
| -i | * | -j | = | k | ||||||
| -j | * | k | = | -i | ||||||
| k | * | -i | = | -j | ||||||
| -i | * | -j | = | k (2.24) |
|
| * |
| = |
| ||||||
|
| * |
| = |
| ||||||
|
| * |
| = |
| ||||||
|
| * |
| = |
|
The last step equals the first.