We use the mechanism of gravitation as is described in page 3 of NEWTON EINSTEIN GRAVITATION, that's our first proposition.
Our second proposition is that if you reverse ALL time arrows in the situation, you obtain precisely the same situation, as stated in item 12 and item 14 at the previous page of this storyline THE EXPANSION OF THE UNIVERSE. (Strictly speaking we should apply the CPT theorem from page 4 of QQD.) So we assume gravitation as we know it exists and we assume the backward time evolving world can exist too.
The third proposition that we use here is that parts of space can be forward evolving in time while other parts of the same space are backward time evolving. Forward and backward time evolution can exist next to each other in the same space.
Both situations exist, forward evolving as well as backward time evolving areas, that's what we agree upon here. This page calculates the border between the forward and backward time evolving areas. It describes how a backward evolving area looks like as observed from a forward time evolving area and it estimates their mutual influence.
In gravitational action vacuum streams inwards matter, dragging along everything that floats
in it. When this process is time reversed, one gets an outward stream that likewise drags everything along with it in outward direction. When one subsequently applies the putting a velocity in a box
method from paragraph Is this all? at page 4 of NEG, then one obtains an outward directed, constant acceleration: a true antigravitation. (1)
But this is not what we want, not there. Regard a planet orbiting a sun. When the film of this is played backwards we still see a planet orbiting a sun, albeit now in the opposite direction. This is not obtained by introducing a repelling gravity.
Vacuum streams out of a dark star. Still we see
a planet orbiting it, a dark planet around a dark sun. (For more about the actual visibility of dark matter, see page 4 *) in the storyline FORWARD BACKWARD TIME DIRECTION.) Against the outflow of vacuum it deviates its track towards the star.
*) IF YOU ARE READING TONE AND READ IT FOR THE FIRST TIME, REGARD LINKS LIKE THIS AS A PREVIEW AND DO NOT VISIT THEM TOO LONG.
Most of them are treated later in TONE. One can recognize a TONE page by the TONE contents table at the top of the page.
In order to prevent their planets being dragged away from their suns, I devised a kind of trick. Imagine a dark planet orbiting a dark sun. At the planet we assume a hidden supply of velocity - all kind of velocities of equal amounts in opposing directions, carefully adding up to zero - from which the outward stream of vacuum erases one. Outward flow of vacuum removes velocity from the planets. The complement velocity, directed towards the dark star, remains and pushes the planet a bit towards the star, thus forcing it in orbit around the star.
Dark flow erases velocity. (2)
A laborious formulation, used to maintain the picture of gravity sketched so far and at the same time create the film of events in backward time direction of dark planets orbiting dark suns, as observed by us.
I am still not happy with this trick. I want the backward time evolving vacuum to drag things that are floating in it, just like forward time evolving vacuum does. And I still think it does. The film played forward exists and so must the film played backward. I only still didn't found a proper way to describe this.
The problem is issued well at the paragraph The sink drain, below at this page.
Maybe a better way to deal with this is using the Dark Multiplication Rules at page 2 of QG. However I didn't apply those rules to the laws of mechanics in a useful way yet. It remains a supposition.
We assume:
There is full symmetry between the forward and backward evolving worlds. (3)
Their laws of nature are identical to ours, that's our starting point. They regard us precisely in the same way as we regard them. (I am still unsure about the neutrinos, whether they see also only left hand neutrinos and right hand antineutrinos.)
There must be a time arrow in the vacuum itself. Let's launch another theorem.
Where time goes forward, there gravitational sagging-in of shells dominate. (4)
Where time goes backward, there antigravitational expansion of shells dominate. (5)
Where gravitation and expansion equal each other, there is the time border. (6)
We state:
BACKWARD TIME EVOLVING MATTER = DARK MATTER (7)
FORWARD TIME EVOLVING MATTER = BRIGHT MATTER
When time is reversed, a matter particle becomes an antimatter particle. This fits in with the CPT theorem at page 4 of QQD.
DARK MATTER = ANTIMATTER (8)
BRIGHT MATTER = OUR KIND OF MATTER
Mark the apology in the column at the right about the use of the expression dark
.
Event A := Event B
means Event A becomes Event B by means of time reversal
. In this page time reversal
means the film of the event being played backwards
.
:=
Forward vacuum
Backward vacuum
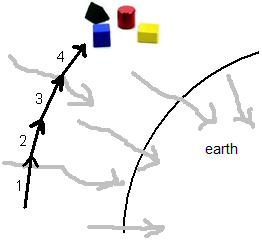
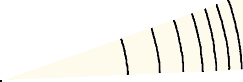
The left picture just below is fig. 5 from page 1 of NEG. There the inward flow of vacuum (grey arrows) adds a velocity increment (perpendicular to orbit velocity) to the blocks that go with the flow.
When gravity is in action, space is disappearing. Shells of vacuum particles after rearranging have smaller surface than before rearranging of the vacuum particles. Space is shrinking when gravitation is in action, observable by all things floating
in the vacuum, being dragged by it.
In the dark matter as we observe it, Higgs particles are emitted in the course of backward time evolving renormalization. The new Higgs particles are immediately absorbed by the vacuum, enlarging it by their volume. Space expands there (despite the erasure of velocity act). The number of vacuum marbles connecting them and us has grown, so there is more space between them and us.
Move the cursor from left to right over the lightgreen-lightblue bars to show the mechanism of gravity as proposed in the storyline NEG page 3, 4 and 5. The left side row of bars, denoted as Forward vacuum
show gravitation, the row of bars at the right side denoted as Backwards vacuum
show the mechanism of expansion of the universe - in fact antigravitation, the gravitation of antimatter.
lightyellow = three dimensional vacuum, consisting of vacuum marbles. For convenience, regard each shell as consisting of a layer of one vacuum marble thickness.
gray = a hole in the vacuum
A = a mass center
Mass A absorbs one or more vacuum marbles (Higgs particles
) from the vacuum, leaving a spherical hole there (cursor at second bar of first row, shown is a gray triangle-like part of it only)
Shaded = vacuum marbles at the brink of falling into the hole. When they actually do, they leave behind a new, shell shaped hole. Each shell shaped hole has the same volume as the original sphere in the center, so when the surface of the shell increases, the thickness of the shell decreases by the same factor.
(For the shells holds that there is lesser space inside than there ought to be, due to disappearance of one or more vacuum marbles, while the space outside hasn't changed yet. This meets the requirements for a local - and temporal - negative curvature.)
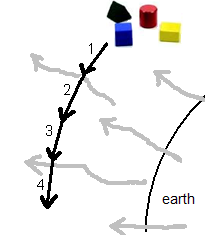
Suppose, in the depths of the nearest void is a cluster of galaxies, evolving backward in time. They are immersed in backward vacuum, they consist of antimatter and they are dark. Regard a dark star there, with some dark planets around it. The mechanism of gravity in backward vacuum as observed by us, is depicted by the second row of bars. As observed by us, it comprises an outward flow that drags by everything floating in it: a repelling gravity. But mind, as observed by us, in backward vacuum the outward flow erases velocity from the dark masses, still making the dark planets to orbit their dark sun.
As observed by them themselves, they are bright. The particles they consist of absorb vacuum marbles and a subsequent inward flow of vacuum drags everything floating in it towards the gravitational centers according to the picture of the first row of bars. The sequence of sagging-in shells proceed outward and finally meets the time border, somewhere in between the void and us. And then, what happens there?
The time border is a plane, a mathematical plane, separating forward and backward vacuum. It is by no means a special place and there is nothing special to see. A photon proceeding in forward vacuum and then entering backward vacuum, traces out a straight line in spacetime, that is our starting point. Also particles show nothing special in their track when passing the border, see also Cross roads, page 6 of FORWARD BACKWARD TIME DIRECTION. Then, since rearranging of vacuum marbles is regarded as a kind of particle reaction, also the outward bound series of sagging-in shells around the dark sun, as observed by them, will pass the border without changing shape in spacetime. (11)
Only the judgements differ. We judge the photon or particle to proceed towards the time border, leave our vacuum and enter theirs - and they from their point of view judge precisely the same!
The time border itself is a mathematical plane, it does not consist of anything special. Just at our side of the timeborder, there are forward vacuum marble pairs equaling 1 (Here we run ahead from knowledge about Quaternions.) and, just at the other side of the time border, there are backward vacuum marble pairs equaling -1 and that's all there is to a vacuum. We conclude the border is seamless. For more about the time border, see page 4 and 5 in the storyline FORWARD BACKWARD TIME DIRECTION.
When the sequence of sagging-in shells around the dark star as they observe it, passes the time border and enters our vacuum, then we judge the sequence as an outward flow, an antigravity. IF the sagging-in of shells in our vacuum drags by masses floating in it (constituting gravitation) THEN the inward bound series of outward expanding shells in our vacuum is dragging by masses in precisely the same way. What is ordinary gravity in their vacuum, becomes repulsive gravity in our vacuum when the expanding expanding shells have passed the time border to our side of it. (12)
We don't observe erasing of velocity at our side of the time border, neither from our own sun nor from the gravitational field of the dark star. We observe repelling gravity from dark matter far away.
Recall that the dark cluster of galaxies is in the nearest void. And there is the cluster of galaxies we are in. Between them is what we could call the Large Time Border (LTB). When at our side of the LTB a mass falls with increasing speed to the bright mass of our cluster of galaxies, due to their gravity. This velocity is now increased by the gravitation originating from the dark masses at the other side of the LTB that is repulsive as soon as it has passed the time border to our side.
Without any propulsion you cannot stay at the time border. (13)
In case of two matter galaxies there is a point between them where the attractive forces of both galaxies cancel each other out. But in the case of a matter galaxy and an antimatter galaxy of equal mass the forces to deviate anything, bright or dark, away from it, are twice as strong as the gravitational force of one of the two galaxies alone. A point of zero force does not exist at the time border. This keeps the time border free from anything hanging around there. There is very little matter (or antimatter) there to show the LTB. Dark matter (in the sense of backward time evolving matter) remains well hidden! (14)
Backward time evolving matter - dark matter (no capitals) as we call it from now on - is a candidate for the Dark Energy. (15)
It explains the Dark Energy, the capitals indicating that we mean here the accepted cause of the acceleration of the expansion of the universe. It does not explain the expansion of the universe.
For a test mass m on the time border between mass M and mass bM holds:
( b is a real number larger than 2, d is the distance between M and bM, all masses are point masses )
G * m * M / r
= G * m * bM / R
1 / r = b / R
r * b = R
(x + y + z) b = (d - x) + y + z
= x - 2xd + d + y + z
(x + y + z) (b - 1) + 2xd = d
x + y + z + 2xd / (b-1) = d / (b-1)
(x + 2 * x * d/(b-1) + ( d/(b-1) ) - ( d/(b-1) ) + y + z = d / (b-1)
(x + d/(b-1) ) + y + z = ( d / (b-1) ) + d / (b - 1)
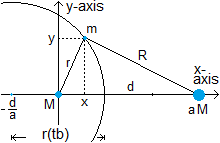
(z-axis not shown)
b-1=a, b=a+1, a is larger than 1
For a test mass m on the time border between mass M and mass aM holds:
(x + d/a ) + y + z = d / a + d / a (21)
The time border is a sphere around mass M with radius r(tb) = SQRT( d/a + d/a ) and off-center over distance d/a; Take d=1 so r(tb) = SQRT( 1/a + 1/a )
| a
| 2
| 3
| 4
| 5
|
| 1/a
| 0.50
| 0.33
| 0.25
| 0.20
|
| r(tb)
| 0.87
| 0.67
| 0.56
| 0.49
|
| r(tb) -1/a
| 0.37
| 0.34
| 0.31
| 0.29
|
When a is very large then the time border is a sphere of radius r = SQRT( d/a ) = d / SQRT a
and M is in the center of the sphere. (22)
Regard an antiquark in an antiproton at the Earth surface. There is a bubble of backward time evolving vacuum around the quark of radius r. Then a = 3.57 * 10^51 * 3, that is the number of nucleons the earth consists of (see calculation of the vacuum marble radius) times 3 (there are 3 quarks per nucleon) and d = the radius of the Earth = 6.38 * 10^6 m. The radius r of the bubble
= d / SQRT a
= 6.38 * 10^6 / SQRT( 3.57 * 10^51 * 3 )
= 6.2 * 10^-20 m.
In its own frame, in its tiny bubble, the antiquark absorbs a vacuum marble in the course of renormalization. In our frame this bubble is experienced as a backward time evolving vacuum wherein the quark did emit a vacuum marble. The emission causes shells around the quark to expand (the time reversed version of sagging-in of shells) that nevertheless erases velocity from present particles (if there were particles inside). Once outside the bubble, the expanding shells are repulsive gravity indeed. (23)
Compare this to the radius of the proton that is (a little less than) 10^-15 m and the vacuum particles that are supposed to maintain a relative distance of between 10^-20 and 10^-21 m. So the backward bubble around
an antiproton at the earth surface is about 10 to 100 vacuum particles across and is residing as a tight jacket around the quark that emitted (in our frame emitted) the mentioned Higgs particle. So for 1 antiproton at the earth surface even between the antiquarks the vacuum is still forward. No anti-entropic behavior to be expected there! (24)
The mass of the quark. There is little known about the quark mass. The mass of a quark might be larger than the mass of the proton and being reduced by the so-called mass defect when the 3 quarks clump together. The mass of a quark might be smaller than 1/3 of the mass of the proton and then being enlarged by its high average speed in the proton and special relativity. But we don't have to know the mass of the quark, we only need the ratio between the number of quarks in the Earth and in the quark (1 of course). We don't isolate that single quark. It is thought as to keep its presence within the baryon and so we assume no further corrections are necessary.
Only when the number of clumped together antimatter atoms grows, they first conquer the space in the antiprotons, then win backward vacuum in the atom's volume, and finally occupy the space between the anti-atoms and anti-molecules. And then anti-entropic behavior is expected. (25)
What happens then is worked out at page 7 of FORWARD BACKWARD TIME DIRECTION. Time border behavior is worked out there. But you better start reading page 4, skip The Diamond
from page 5 and then read page 6 and 7.
An antiproton - its own gravitational field negligible - falls in the earth’s gravitational field just as a proton would do (well, nearly as a proton would do), compare the dark snowball in paragraph 6 below. And likewise when an electron-positron pair emerges, they are supposed to be separated from the first moment and to obey forward vacuum behavior.
If one has followed argumentation in page 3 and 4 of NEG then it is clear that by the absorption from the Higgs field and subsequent action of gravity, vacuum is shrinking. While at the same time the backward time evolving vacuum by the emission to the Higgs field, is expanding. As a consequence the time border (the border between forward and backward evolving areas) starts moving towards forward time masses, and away from backward time masses, as observed by us. While the calculation above shows the time border not to be dependent of time. So I assume it is time for another theorem:
The time border is at the specific place where it is calculated to be. When vacuum particles are pushed over the time border from backward time evolving space into forward time evolving space, the pushed-over vacuum particles change from backward to forward evolving in time. (26)
In doing so we assure the time border to remain stable at its calculated position.
We now run a little ahead of the storyline so far.
If the vacuum marble is a structure, it changes into its enantiomer, when passing the time border. (27)
See (2.13) and (2.14) in Building vacuum from gluons at page 2 of QUATERNION GRAVITATION.
When dragged by the streaming vacuum, a particle doesn't notice it is dragged by. One single particle has its structure, its shape, relative to the vacuum. So, if the vacuum itself is mirror-imaged, I assume the shape of the single particle is mirror-imaged along with it, not noticing something had changed. When passing the time border all four xyzt coordinates are mirror-imaged, see (2.13) and (2.14). Swap of the sign of the time coordinate makes the spin of the particle to reverse. Changing the particle in its enantiomer swaps the spin back again. After all the spin of a particle doesn't change when passing the time border. (28)
This inspires to a new theorem:
When regarding the spacetime diagram, one sees nothing special happening at the time border. (29)
There are no observable events at the time border that show passages through it.
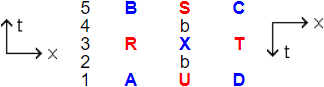
bbbbb is the time border, behind the S, X and U there is another b
(30)
After traveling AX (that means from A to X) the choices where to go seem to be XD or CX. Here XD (from X to D) is the usual scifi choice of going backward in time, leading to a wealth of paradoxes. This way we don't go. We take CX (from C to X) as a second possible way of going backward in time.
If the shown part of spacetime is void of everything and then a particle or object moves AX at constant rectilinear speed according to the first law of Newton, then the part of the track behind the time border that fits in with it, is CX. (31)
I investigated this at page 4 up to page 7 in the storyline FORWARD BACKWARD TIME DIRECTION. Skip The Diamond
at page 6, which is the usual scifi approach.
The act of gravitation always returns to flat Minkowski spacetime. Also the act of antigravity returns to flat Minkowski spacetime. Renormalization procedure, in forward as well as in backward evolving time, performs with respect to the flat grid. The act of gravitation simulates **) positive curved space (spherelike) for all phenomenons whose effects sum up in the course of time. The act of antigravitation from the antimatter, when it has reached our forward time aereas, simulates negative curved spacetime (saddle-like). The positive and negative simulations tend to cancel each other. (32)
Observations show the overall curvature might be zero, denoted by 
= 1. This might indicate that
The amounts of matter and antimatter in our universe are more or less equal. (33)
**) Simulation doesn't mean there is no effect. A planet can still be torn apart by the tidal forces from its sun when in a too elliptical orbit and too near around it. Black holes are still formed. And so on.
When the e+ e- coincide sufficiently to a pair, they form a composite. The proton mass is about 2000 times the electron mass and at the earth surface the distance r becomes SQRT 2000 or about 50 times smaller. So by coincide sufficiently
we mean: within a distance of about 10^-20 m and this is near to the highest resolution the vacuum marbles can support.
1
The electron absorbs Higgs particles from the vacuum. The positron inside the time border, as observed by us, emits Higgs particles at the same pace. ***) As a consequence the composite does not absorb nor emit Higgs particles and thus is massless and has zero gravitational field. (41)
Since the composite has no mass, it immediately gains lightspeed. The two composing particles force each other along the same path, because the slightest separation (10^-20 m) would separate the forward and backward vacuums and then the electron and positron would get mass, for which the energy is lacking. (42)
By now the composite of the electron and the positron is resembling the photon too much to ignore. See more about it at page 5 of the storyline NET FORCE IN QED. (43)
***) In fact it turned out just the other way around: positrons are the particles and electrons are the antiparticles. See Electrons as baryons at page 4 of QG.
2
If number 1 is the photon, then also the gluon might consist of a quark and an antiquark, massless coinciding. The spin-story would be identical. The electric charges would cancel likewise. If the taste of a quark is u, then the taste of its antiquark must be anti-u, and u and anti-u should cancel then to zero taste. See more about this in paragraph Meson exchange at page 4 and especially Four quarks in the shell at page 5 of the storyline QCD. (44)
3
This tric can be performed still once more. A neutrino and an antineutrino of the same family should be able to coincide massless. This would yield a new type of radiation, that I would like to call neutrinophotons. However, spin 1 neutrinophotons turn out not to exist. But spin 0 neutrinophotons would. See paragraph Neutrinophotons at page 4 of the storyline QG. (45)
What happens when two planets of equal mass, one bright, the other dark, pass each other by? For convenience assume equal radius too. There is outflow of vacuum from the dark mass and inflow of vacuum into the bright mass. At all times the outflow of vacuum from the dark mass equals precisely the inflow of vacuum into the bright mass. As a consequence there is only a flow of vacuum between the planets. The amount of vacuum between the planets remains the same. They will not change each other's motion, they will not deviate each other’s paths. They will pass by each other with constant rectilinear motion, their orbits just any pair of straight lines. They feel no signs of their mutual passage - as long as they do not collide, of course (matter-antimatter explosion). (51)
When relative velocity is zero, they will keep on hanging there, motionless relative to each other. (52)
Visibility depends on the light source. In the light of the dark sun you will not see anything. Our eye is not adapted to light that is drawn
from us, instead of light entering the eye. In the light of a matter sun or the lights of your ship you will see both planets (dark and bright) alike. More about this in The dark meteorite at page 4 of FORWARD BACKWARD TIME DIRECTION. (53)
Two stars of equal mass, one dark, one bright, will act like the planets do. A dark star cannot orbit a bright star of equal mass. (54)
Compare the vacuum, the sagging-in of shells and dragging by of all that floats in it, with a conveyor belt. Since the velocity of the belt out of the dark planet equals the velocity of the belt into the bright planet, there is no tendency of the belt to reduce nor enlarge their mutual distance. The belt doesn't lengthen nor shorten. (55)
What happens when the bright mass measures e.g. 7 units of mass and the dark mass 3 units of mass, and then they pass by each other? Using the view of the conveyor belt connecting the masses, now 7 units of length of vacuum flows into the bright mass against 3 units of length of vacuum in the same time flowing out of the dark mass. The flow between the masses decreases distance with 7 - 3 = 4 lengths in the same time, constituting an attraction. The force is considerably smaller than with Newtons gravitation law between bright masses.
Now shift view to the 3-units dark mass, so it is bright now. Time runs the other way now, the 7-units is dark now. We see 7 units of conveyor belt streaming out of the 7-units dark mass against 3 units streaming into the 3-units bright mass. The 7-units wins but since its surrounding vacuum is dark it erases velocity. So the gravitations subtract but then is still attractive because the dark vacuum erases velocity instead of adding it. This is laborious, but I see no other way to make things fit.
Imagine a dark snowball, an antimatter snowball of 5.97 kg. From the depths of the void it had made it to the earth, just above the atmosphere. The mass of the Earth is 5.97 * 10^24 kg. Imagine the conveyor belt. For every 10^24 meters of conveyor belt streaming into the earth, is there about 1 meter streaming out of the snowball?
In The calculation of the time border will be derived that the time border around such a snowball is not there. There only are very tiny time borders around each quark. As far as is concerned their mutual gravitational influence, even the antiquarks react bright at the Earth surface. This doesn't withhold the gravitational force from the dark snowball to be repulsive, as observed from our point of view. As observed by us, the quarks the snowball consist of, emit to the Higgs field, causing expanding shells, a repulsive gravity. As long as this enlarging of space is behind the time border (behind from our point of view), it erases velocity. However, very soon it has passed the time border around each quark and then it is just repulsive gravity that is left.
So the dark snowball is dragged along with the gravitational field of the earth, just a tiny little bit slower than a bright snowball would do (1 meter conveyor belt streaming into the bright snowball against 1 meter conveyor belt streaming out of the dark snowball). The behavior of a dark snowball in the earth atmosphere is nearly precisely that of a bright snowball. Both snowballs obey bright mechanics, mainly. (Except for annihilation effects of atmosphere molecules on the antimatter snowball.)
So a bright snowball can orbit a dark planet, obeying dark mechanics. Or a rocket can. I can land there. (Not wisely, but I can.)
IF YOU ARE READING TONE FOR THE FIRST TIME, ALL NECESSARY THINGS FOR THE CHAPTERS TO COME ARE GIVEN NOW, YOU CAN SKIP THE REST OF THE PAGE AND READ IT LATER.
And now for the formulas. To imagine what happens, keep in mind two things.
First the picture of gravitation around a bright mass (matter). Sagging-in shells, inward displacing shell content, drag everything in it along with the shells. Around a dark mass (antimatter) expanding shells, outward displacing shell content, also drag everything in it along with the shells. This is the main picture. (56)
Second, there is the time border, a mathematical plane separating forward and backward vacuum. Forward vacuum is the vacuum we know. In backward vacuum the laws of physics are different. Velocity is erased there to keep planets in orbit, see paragraph 1. The multiplication is different, -1 times -1 equals -1 there, see paragraph 2. (57)
Gravitational force is a vector. If vectors are given in bold, the Newton gravitational law for matter in bright vacuum is:
F = G * M1 * M2 * r / r^3 (58)
which is just the well-known gravitational law F = G * M1 * M2 / r multiplied by r/r, a unit vector made from the vector r that points from point mass M1 to point mass M2.
Instead of this we better use gravitational field strength g (gravitational force on a point mass of 1 kg). Set M2 = 1 kg.
g = G * M1 * r / r^3 (59)
In this site we will use g/G and equal that to M1 / r times the unit vector r/r.
g/G = M1 / r * r/r. (60)
This is the field strength around M1 (and caused by M1), r is the vector pointing from a point you want to know the field strength of to M1.
With this formulas we are not yet able to reproduce (41) and (42). It is not true that between two planets of equal mass, one bright, one dark, at every point the amount of sagging-in cancels the amount of expanding-outward. (So when a planet rotates sufficiently fast around its axis and the planets are near enough to each other, then tidal effects are expected!) But one can image that, from the vacuum between the planets, the total decrease of vacuum by the bright planet cancels the total increase of vacuum by the dark planet. And since the amount of vacuum between them doesn't change, their relative distance is maintained.
As said, we better talk about gravitational field strength instead of gravitational force:
g/G at the location of a bright test point mass m caused by a bright mass M1 and a dark mass M2 is:
g/G = M1 / R * R/R + M2 / r * -r/r (61)
where R is a vector pointing from m to M1 and r is a vector pointing from m to M2. So m is in O, the Origin. It is precisely the same as force in the usual Newton gravitation law. The force F on m is
F = G * M1 * m / R * R/R + G * M2 * m / r * -r/r (62)
The actual effect of the gravitational force from dark matter is repulsive only in bright vacuum. In the dark part of the vacuum it erases velocity.
Are the orbits of the masses elliptic? And if velocities too high, hyperbola's?
Original text, start
The formula for the gravitation F between the dark and the bright mass seems to be:
F = G ( m-bright - m-dark) / r (63)
r being their mutual distance, G = gravitational constant. When m-bright = m-dark then F = 0.
Mechanics, dark and bright together.
But I should not be surprised when the formula turned out to be:
F = G ( m-bright / m-dark) / r (64)
When m-bright = m-dark then F = G / r, which for planets is also about 0.
If (53) is right, then a particle and its antiparticle don’t annihilate under the force of gravity since particle and antiparticle have equal mass. They exert no gravitational force on each other.
When (54) is right, a particle attracts its antiparticle by a gravitational force F = G / r, becoming as strong as the particles are permitted to approach each other before actual annihilation.
Original text, stop
Don't you see
Don't you see
Regard again the two identical planets M1 and M2, one bright, one dark, and suppose them at rest relative to each other. As said, they stay at rest relative to each other. The time border between them necessarily is the flat plane halfway between them, perpendicular to the line connecting the planets. Regard the point at the bright side (in bright vacuum) nearest to the cross point of the connecting line and the time border. There the force of both planets are equal and work in the same direction. Everywhere along the route from M1 to M2 the acceleration is the sum of accelerations working in the same direction and proportional to M1 / R + M2 / r. When free floating and put at rest relative to the planets, a test mass m cannot remain standing still on the time border.
One can launch mass m straight up to the other planet. While climbing it reduces speed and we can launch it such that precisely at the time border it comes to a standstill. The next moment it starts falling back, in a time-reversed version of the climbing path. Eventually mass m doesn't climb completely straight up but in a kind of elliptical orbit. Then, when one moment being tangential to the time border, it would just complete its orbit. (I am not sure the orbit is elliptical.)
When starting speed was just a little higher, we observe mass m to pass the time border and fall with increasing speed to the dark mass. Mind, at the dark side the force erases velocity. Finally m collides with the surface in a matter-antimatter explosion. But well, it is not precisely an explosion.
In fact m doesn't fall to the dark planet, despite we observe it so. Evolving backward in time we know m being launched from the surface of the dark planet. As they observe it, in an anti-entropic fashion an antimatter mass m is drawn from
their planet's surface and speeds upward, reducing speed while climbing.
Since free floating, matter mass m, as we observe it, reduces speed when climbing to end at some none-zero speed at the time border. It ends its evolution there. It clicks on to the course of events of mass m at our side being launched towards the time border.
To be frank, mass m has no natural source at M2. So at the time border there exist a superposition of all possible ways m could have come to existence there. From the superposition then is taken the most likely event, that's the way it usually happens. The described course of events is not the most likely, maybe.
Similar considerations are made in The time border, page 4 of FORWARD BACKWARD TIME DIRECTION, and page 6 and 7 of the same storyline. Skip The diamond
at page 5.
A similar problem like this in item 13 of page 3 of the storyline FORWARD BACKWARD TIME DIRECTION is the following.
Imagine a large shallow lake with in the middle a large sink drain. Water violently flows away through the drain, causing a radial stream of water onto the middle of the lake.
Or imagne a small Niagara Falls, however not a straight wall of water in a river but a closed circular wall of water in a lake. We assume the radial stream in the lake is without vortices. (I am not sure this is feasible with a real lake, but assume it to be so here.)
Then a jetski circumvents the rim of the cirular falls. It steers straight forward with constant speed and perpendicular to the stream. The stream drags it sideways toward the falls. The velocity of the jetski is precisely such that the jetski not escapes into the open, nor is it dragged in the Falls. The jetski keeps on circumventing the pool at constant distance of it center at constant speed.
Now time is reversed. The water streams out of the drain now, or the falls speed upward and push the water present there aside, pushing the jetski away from the drain. The jetski still can circumvent the drain by steering sufficiently toward its center, at an angle with the direction perpendicular to the stream. But I want the reversed sequence of events of the original situation. Why doesn’t that work? (67)
O
NVESTIGATE
Maybe more advanced techniques hint for a solution.
Elie Joseph Cartan, 1869 - 1951, found solutions to the Einstein equations with torque-description. These were equal to Einstein’s but more complex, so they chose Einstein’s. (68)
Observed from the dark planet - time runs the other way now - there is nothing special there. Vacuum is flowing into the dark star, it drags the dark planet along with it and because of the planet’s velocity it orbits the star. They experience themselves as bright. If they look up to the sky they see us, our kind of matter, as being dark. They don’t see us. So they don’t have to observe the earth’s velocity to deviate towards the sun while vacuum is streaming out of the sun, as they observe it. (69)
Imagine bright planet M1 and dark planet M2 sufficiently far from each other to cause no significant tidal effects. Suppose the planets don't rotate around any of their axes and just hang there motionless with respect to each other. Where the line connecting their centers crosses the surface, a platform is laid, its perfectly flat surface precisely perpendicular to the connecting line. A bouncing ball with sufficient energy bounces up and down between the platforms, from planet to planet all the time. But no, let's not start with such an entropic thing as a ball (temperature rises in an atmosphere, radiation is emitted in empty space). We start with one single particle. No, we start with one single photon. We know its speed and it has no trouble with the antimatter composition of the platform at M2.
O
NVESTIGATE
