This page is in the colorshift approach mixed with quaternion parts. The quaternion part always starts with the word QUATERNIONS in red and ends with ----- END OF QUATERNION APPROACH -----.

This page starts as if you had red the pages 1 and 2 of the QCD storyline, so maybe you do so.

What happens when the magenta-to-cyan-gluon meets the yellow quark first? One would expect the yellow to absorb the gluon with its +2/6 turn and then change into cyan. The magenta has already been changed into cyan and the original cyan remains unchanged then. That would leave the antibaryon with three cyan quarks, which is color-neutral by no means and this is forbidden. The magenta-to-cyan-gluon will pass by the yellow quark without interacting with it until it meets the cyan quark. There is just no other choice.

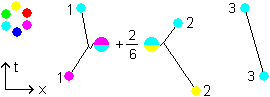
Fig 3.1. Identifying with . Only the +2/6 shift counts.

The same effect happens with the other five possible color-exchanges,

+2/6 from to ,

-2/6 from to ,

+2/6 from to ,

-2/6 from to ,

+2/6 from to .

Therefore it is as if each gluon is bound to the specific start- and end-colorstates of the two quarks it works between. But I suspect strongly that the urge for colorneutrality is the only drive here.

Therefore I would suggest that any quark can always absorb any gluon. When a quark absorbs a gluon, the change of color of that quark is given only by the gluon's shift of color along the colorcircle. This shift can be +2/6, zero, -2/6 and at the end of this page we consider the shifts +1/2, -1/2, +1/6, -1/6. The non-fitting gluons, like absorbing , always yield coloured states that don't occur in nature. Accidentally only the fitting color-changes like absorbing will happen.

What happens when the magenta-to-cyan-gluon meets another gluon first? (Fig. 3.2) The magenta quark has just turned into cyan because of emitting this gluon. There is one other cyan quark left - as long as it hasn't met our gluon - and a yellow one. Assume the yellow one - for the moment not needed in this gluon reaction - has emitted a yellow-to-magenta-gluon . Instead of reaching their goals the gluons meet each other and form a composite:   +2/6 +2/6 = a shift of +4/6 turn = -2/6 which turns out to match the gluon. This gluon is absorbed by a cyan to turn it into a yellow. (Absorption of by a : in normal representation the cyan in the lower part of the gluon is not cyan but anti-cyan. This anti-cyan annihilates with the cyan of the quark, leaving only the upper-color yellow to the quark.)

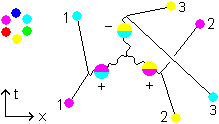        Fig. 3.2

Fig. 3.2 in QUATERNIONS (use the gluon table)

* = -k * -i = j           (1)

* = -i * -k = -j           (2)

(1) and (2) superpose and cancel out,

(j) + (-j) = 0

In fig. 3.2 the shown outcome = -j is only one of the two outcomes j and -j.

----- END OF QUATERNION APPROACH -----

So it seems we can infer from this the rule:

* =

In the two-gluons-composite it is as if the upper magenta from the first gluon and the lower magenta of the second cancel out each other and from one new gluon of the remaining upper and lower color.

What is the spin of the two-gluons-composite? When both gluons have equal spin this yields +1+1=+2 or -1-1=-2. When the gluons have opposite spin this yields +1-1=0 or -1+1=0. But one can hide an extra spin in the orbital momentum of the two gluons. This shall be such that the net spin ends at +1 or -1. Otherwise the reaction will not occur.

(Here the gluNon concept is born, see page 7 of this storyline.)

(In fig 3.1 is not * = , since there is only one gluon there, identified with two different descriptions.)

The next possible scheme is

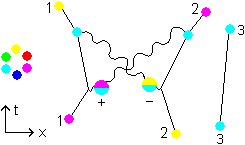Fig. 3.3

We start from the magenta quark having just turned into cyan because it emitted a . Suppose the yellow quark changes into cyan too by emitting a . Then there are three cyans in the antibaryon and two gluons. Suppose the gluons couple: +2/6 - 2/6 = a result having no shift at all. This composite cannot change any color since it has no color shift. It would leave the antibaryon with three cyan quarks which is forbidden. So - provided the coupling will be allowed and provided no other changes are initiated in the mean time - this composite will roam through the antibaryon until the gluons depart again. Then one of the two gluons will meet one of the three cyan quarks and change it to the color of its upper half (m or y). If the other gluon left meets the same quark it will change it back into cyan - since it has the opposite shift - which would leave the antibaryon with three cyans again. This will not happen. It will pass by that quark until it meets one of the other two cyans. Then the antibaryon is white again.

Can this no-shift-two-gluon-composite exist? The lower colors are the same and the upper colors are the two remaining colors.

When we go for the rule that only the shift counts, one can identify this composite with the gluon . This gluon is white. Remember the normal representation. There the upper half of the gluon is cyan and the lower half is anti-cyan, or red. There is no magenta in the gluon, nor yellow. There is cyan and an even amount of anti-cyan. So this gluon is white. If created it can leave then the antibaryon without any obstruction, leaving its quark-parents to their own color-problems, regretting they have ever created him. It would leave the antibaryon with three cyan quarks which is forbidden. We can trust nature will prevent this creation from arising. The two gluons will not couple to yield a white gluon.

Fig. 3.3 in QUATERNIONS (use the gluon table)

* = -k * j = i           (3)

* = j * -k = -i           (4)

(3) and (4) superpose and cancel out,

(i) + (-i) = 0

----- END OF QUATERNION APPROACH -----

From this follows the rule

* = zero =

The next possible scheme is

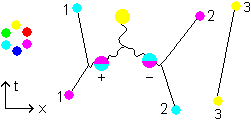Fig 3.4

We start again from the magenta quark turned into cyan because it emitted a . The cyan simultaneously emits a . The sum of the shifts then is +2/6 -2/6 = zero shift. The two gluons will couple and cancel each others colors out to a zero-shift white composite particle. That particle can be identified with - for reasons of symmetry - the white gluon . The magenta and cyan quark are left having interchanged their colors, the antibaryon is left behind white. Then the leaves the antibaryon.

* =

The energy embodied by each of the emitted gluons yields a particle there, probably a white gluon, but there is not really a reason why it shouldn't be a photon or a Z0 (weak force particle). Possible spin-sums for the composite:

+1 gluon -1 gluon = spin 0,

+1 gluon +1 gluon = spin +2,

-1 gluon -1 gluon = spin -2, and these spins do not fit for a gluon, even not a white one. When the orbital momentum of the gluon-composite is +1 or -1 then this can fit with one particle. With no orbital momentum it can fit with two particles, 2 photons or a photon and a Z0. For two Z0 or a W+ and W- more energy is needed.

So two quarks 1 and 2 can interchange their colors by one gluon from 1 to 2, or one gluon from 2 to 1, or both these gluons simultaneously and meeting each other and cancelling each other out. This last reaction takes the energy of the particle yielded in annihilation. So it can only occur in excited gluon-states and not in the ground-state.

Fig. 3.4 in QUATERNIONS (use the gluon table)

* = -j/-i * -i/-j = -k * k = 1           (5)

* = -i/-j * -j/-i = k * -k =1           (6)

(5) and (6) superpose...

1 + 1 = 2

...and doubles the value in the wavefunction.

So this reaction occurs when energy is sufficient and spin can be arranged.

This reaction indeed does yield a glueball (a glue1ball, or if the gluons don't merge, a glue2ball).

----- END OF QUATERNION APPROACH -----

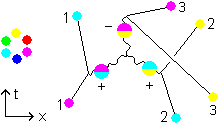         Fig 3.5

The last possible scheme in which the magenta quark emits a that meets one another gluon. The original cyan simultaneously emits a . The gluons meet and form a composite: +2/6 +2/6 = a shift of +4/6 = -2/6 which turns out to match the that is absorbed by a yellow to turn it into a magenta.

This is completely analogous to Fig. 3.2.

Fig. 3.5 in QUATERNIONS (use the gluon table)

* = -k * -j = -i           (7)

* = -j * -k = i           (8)

(7) and (8) superpose and cancel out,

(i) + (-i) = 0

In fig. 3.5 the shown outcome = -i is only one of the two outcomes i and -i.

----- END OF QUATERNION APPROACH -----

* =

We have had now all possible schemes beginning with changing into and with one or two gluons. The schemes beginning with changing into with one or two gluons, all yield analogue results. It gives precisely the same reasoning with the same kind of results.

The colorcircle is fully symmetric. It has no begin or end. Every color is as fundamental as one of the five others. So all reasoning up until now will yield the same results when you shift every color everywhere +2/6 of a full turn. Or shift them all over -2/6 of a full turn. The colorcircle is invariant to overall shifts. So all other possibilities starting with a quarkcolor and finishing with another one with one or two gluons working, are included.

Summary of what we have met until now

minus + plus .

The two involved quarks interchange color. (Here minus means emits and plus means absorbs.)

minus + plus

It passes by the until it meets the

minus + and simultaneously minus +

The gluons couple and merge into -

+2/6 +2/6 = a shift of +4/6 = -2/6

minus + and simultaneously minus -

The coupling of these gluons is prevented.

+2/6 - 2/6 = zero shift =

minus + and simultaneously minus -

The two gluons annihilate to a colorless particle.

minus + and simultaneously minus +

The gluons couple and merge into -

+2/6 +2/6 = a shift of +4/6 = -2/6

* =

* = zero =

* = zero =

* =

So far we did not run into trouble when predicting the outcome of gluon-couplings by the sum of their color-shifts only. We identified one gluon with a different one that turned out to have the same color-shift. We identified the sum of two gluons with a different one that turned out to have the same color-shift as the sum. A gluon-sum with no color-shift turned out to yield a colored state of the antibaryon and so will not occur. Another gluon-sum yielded a white state for the gluon and the antibaryon.

So we can forget about the colors of the gluon and use its color-shift only. It will be calmer to the eye and give a clearer view of what is happening. We can use some clarity. At first I tried to give some by shifting to the time-symmetric representation of gluons. But sometimes, when a quark absorbs a gluon, it is useful to remember the normal representation of the gluon as upper color and lower anticolor. Anticolors can be denoted as one of the 3 colors r, g, b with a dash above it, the usual way to denote antiparticles. But we have chosen to use 6 colors instead of 3 to bring in some liveliness after the grey world shone upon by the white light of QED. And to do more right to the full symmetry between the two color-trios.

In QUATERNIONS the equalities of this paragraph - and the next - give a quite different outcome most of the times. Take e.g. the gluon . Look it up in the gluon table and see that its quaternion value is -j / -i = k and write down “k” instead of the gluon. Do so with all the gluons at both sides of the equation. The equations you get then will usually be wrong, in quaternions.

----- END OF QUATERNION APPROACH -----

Identifying gluons of the same color-shift

We identify:

+2/6: = =

-2/6: = =

zero: = =

From this follows by example

+2/6 +2/6 = a shift of +4/6 = -2/6 shift =

In fact follows

= = = * = * = *

and

= = = * = * = *

Finally there follows too

= = = * = * = *

Other colorshifts and mesons

Up until now we have had the 3 colorshifts +2/6, 0, -2/6 times a full turn along the colorcircle. Between the 6 colors in the colorcircle 3 other colorshifts are possible. First there is colorshift +3/6 (or -3/6, which is the same) that occurs in mesons.

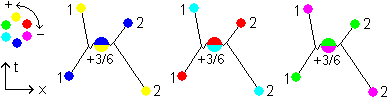         Fig 3.6 mesons

The other 2 are the colorshifts +1/6 and -1/6. There are 6 gluons with colorshift -1/6:

There is little point to the emission of 1 colorshift +1/6 or -1/6 gluon in mesons or hadrons. The end result will by no means be color neutral.

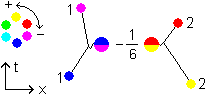         Fig 3.7, meson

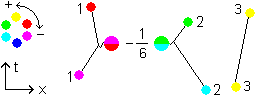         Fig 3.8, hadron

When both quarks of a meson emit a shift -1/6 gluon, the meson that is left behind is color neutral.

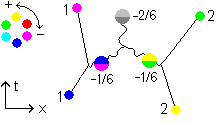         Fig 3.9

But where go the two -1/6 gluons? When they combine to form a -2/6 gluon then where does this go? The colors of the resulting gluon are not clear. These are the 6 shift -2/6 gluons:

One of them have to be the fitting one - when it are more than one these possibilities will go in superposition. But this reaction thus will not occur since the result isn't colorneutral. There is a net colorshift of -2/6.

Fig. 3.9 in QUATERNIONS (use the gluon table)

* = i * i = -1           (9)

* = i * i = -1           (10)

(9) and (10) superpose...

(-1) + (-1) = -2

...and double their value in the wavefunction.

The meson has changed from to .

The resulting mesonic gluon escapes, since it has no color and does not leave behind a colored situation. Its quaternion value is -1.

The free mesonic gluon is a glueball-like object with the ability to apply a CPT-like transformation on any quark or antiquark it encounters. It multiplies the quark's color by -1, changes the direction of time and swaps its spin. When an ordinary glueball (quaternion value +1) is called white, then the free mesonic gluon (quaternion value -1) can be called a black glueball. This is a new kind of particle within the reach of the standard model, predicted by the quaternion approach.

The black glueball is supposed to be the only gluon with mass, see (8) in Building vacuum from gluons at page 2 of QG.

Paragraph Multiplication order at page 3 of storyline QQD says that a glueball can be absorbed by a quark in an ordinary baryon or antibaryon or meson, as long as it leaves behind a color product end state 1 and a color sum end state 0. However, let's look how this general rule works out in practice. The black glueball has color -1 and when it is absorbed by one quark in a baryon, it changes the color of that quark into its opposite color, without changing the electric charge: it still is a quark but now has antiquark color. This is forbidden at the same page 3 of QQD, in (3.41) in paragraph Mesons. Moreover, the baryon now has two quarks with color and one quark with anticolor, so the baryon is no longer white. In mesons the absorption of a black glueball give likewise problems. So a black glueball will not be absorbed by any quark in a meson or baryon. This gives rise to mark the black glueball as a candidate for Dark Matter (mind the capitals), which is also mentioned in the column at the right at page 2 of THE EXPANSION OF THE UNIVERSE. And mind the mass of the black glueball, its energy, has to remain somewhere.

The two gluons in fig. 3.9 are sole until they meet to form a gluon pair of quaternion value -1. (Supposed is gluons can form pairs, a sort of circling around each other without merging. This runs ahead on page 7 of this storyline, GluNons.) They are not absorbed by the vacuum (the vacuum has quaternion value +1, see QG, page 2, paragraph Filling in the vacuum marbles). The only possibilities for the two sole gluons from fig. 3.9 are to pass each other by (see fig. 3.12) OR to resonate between the -1 gluon pair state (gluons not merged) and a free mesonic gluon state (gluons merged). The main reason it isn't formed abundantly might be its creation costs so much energy that this usually cannot be afforded.

Moreover, two spin-1 particles couple less easy than 3, according to page 7 of this storyline. In this case a kind of spin orbital momentum has to cancel the surplus spin in the glu2on for the resonation to occur. This reduces the mentioned resonation to orbital momentum 1 glu2on states, the orbital momentum 0 states do not participate here.

Let's replace the two gluons of Fig. 3.9 by two baryonic gluons: the 2 quarks of a meson emit 2 baryonic gluons simultaneously.

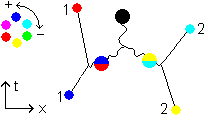Fig 3.10                     

* = j * j = -1           (11)

* = j * j = -1           (12)

The meson has changed from to

(11) and (12) superpose by (-1) + (-1) = -2 and double their value in the wavefunction. The resulting particle is a free -1 mesonic gluon, a black glueball.

Another example. The two quarks of a meson emit two mesonic gluons simultaneously.

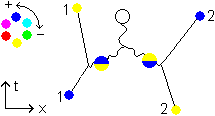Fig 3.11

* = -1 * -1 = 1           (13)

* = -1 * -1 = 1           (14)

The meson has changed from to , the usual color swap in mesons.

The two mesonic gluon multiplications (13) and (14) superpose by 1 + 1 = 2. They double their value in the wavefunction too and yield a white glue1ball.

----- END OF QUATERNION APPROACH -----

Another scenario arises. The 3 quarks of one hadron each emit a -1/6 gluon that combine to a -3/6 mesonic gluon. A neighboring hadron produces a +3/6 mesonic gluon along the same route. The 2 mesonic gluons combine to a white glueball. And the two hadrons now each have 3 anticolors instead of colors. So that is possible and if not for the rarity of the process it would regularly happen.

A reaction with colorshift +1/6 and/or -1/6 that can exist is:

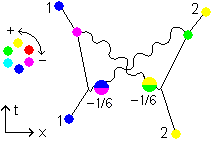         Fig 3.12

So the colorshifts +1/6 and -1/6 do contribute. But most of the diagrams shown so far do not have a counterpart in +1/6 and -1/6 colorshifts because the result is not colorneutral. Colorshift +2/6 and -2/6 are hadronic shifts. Colorshift +3/6 is the mesonic shift. The colorshifts +1/6 and -1/6 transform a color into an anticolor, but not the anticolor of the color but one of the two other anticolors. The border between color and anticolor is thin. It is merely the reactions with colorshift +1/6 and -1/6 are seldom colorneutral, otherwise there would be far more conversion between colors and anticolors.

The colorshift approach reduces the 9 (in fact 8) independent gluon-fields from accepted QCD to 6 independent gluon-fields: +3/6, +2/6, +1/6, 0, -1/6 and - 2/6. Not a large reduction, but nevertheless.

It seems the computation rules for gluons as quaternions are sufficiently given to make a renormalization calculation possible. That would be the crucial test for the quaternion approach.