Derivation of the field of all possible velocities. Identification of an expanding frame with the field of all possible velocities. Constructing one of the three Higgs fields. A first glimpse of the spin asymmetry in the weak force.
The identical fermion explosion
According to page 3 up to and including page 6 of NEG (storyline NEWTON EINSTEIN GRAVITATION) mass absorption from the Higgs field curves space and the subsequent action of gravity curves it back. Finally gravitation does not curve spacetime. That is to say,
The curve-and-curveback action accompanying every Higgs field absorption yields remnant effects that accumulate and that we observe as gravitation, but the background grid remained flat (virtually flat) all the time (1.1)
Take also into account the existence of the frames of reference of receding galaxies (observed), CMB (observed) (CMB = Cosmic Microwave Background), neutrinos (not observed as frame) and gravitational waves (not observed as frame): non of them are fundamental frames, see also paragraph Standstill at page 5 of THE EXPANSION OF THE UNIVERSE. Therefore I would propose to consider that
The view of the BB (Big Bang) that fits the best, is an ordinary explosion occurring in flat empty space (1.2)
This is treated below in paragraph Remnant particles in the fermion explosions.
Then the BB is not a fundamental feature shaping spacetime. Light waves from distant galaxies no longer arrive while still expanding, as is said in paragraph The universe expands at page 5 of THE EXPANSION OF THE UNIVERSE.
The TONE storyline concludes (especially spoken out in the chapter 4 conclusions and the Epilogue) that
The quark is the only elementary particle existing (1.3)
This opens the possibility that
The bunch of particles the BB consists of, very well might have been identical quarks only, all on the same place (1.4)
If so, then immediately after the BB the particles must obey the Pauli exclusion principle, the demand for fermions that says
Two identical fermions cannot occupy the same quantum state (1.5)
Then it might be at the BB, when started out as innumerable identical elementary particles much nearer to each other than e.g. 0.9 fm, that is chosen for expansion as the fastest way to obey the fermion demand, since then every quark has at least a different velocity. So
The BB is driven by an identical-fermion explosion
(a fermion explosion in brief) (1.6)
(If was chosen for an implosion instead of an explosion, this would have worked too. The imploding identical particles approach each other, go right through each other and then as yet form an explosion.)
The fermion explosion is a quantum mechanical phenomenon. So despite it is regarded as an ordinary explosion taking place in flat spacetime, there still is a fundamental feature at work.
The fermion explosion of the vacuum particles
The BB so far, without saying it explicitly, is regarded as an explosion of matter, the matter of our universe. The already mentioned page 3 up to and including page 6 of NEG show that if one assumes the vacuum to be built of particles, vacuum particles as we call them, gravitation can be concluded. Let's investigate that the fermion explosion not only yielded the expansion of our matter in the universe but also leads to the expansion of vacuum particles.
For the Pauli exclusion principle to work there is needed some space, I guess. I presume the Pauli exclusion principle can be defined in two dimensions and maybe even in one dimension, but not in zero dimensions. Therefore I presume already existing space as is suggested in (1.2), not only for the fermion explosion of our matter, but also for the fermion explosion of the primordial vacuum particles.
If you have an expanding frame and there was one elementary particle in every possible place of it and no particle would have any extra velocity relative to the expanding frame (every particle locally stands still with respect to the expanding frame), then every possible velocity would be possessed by precisely one particle.
Suppose the vacuum particle fermion explosion is very precise. The velocities of the vacuum particles then are determined about 100 %.
The Heisenberg uncertainty relation is:
Δp * Δx  h/2
h/2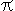 (2.1)
(2.1)
p = impulse, x = position, h = constant of Planck
Therefore, according to this uncertainty principle the locations of the velocity of each vacuum particle in the fermion explosion are uncertain about 100 %. Each velocity with its precise direction and precise magnitude can have any location. This doesn't affect the velocities themselves, all velocities are supposed to maintain magnitude and direction, only the location becomes completely uncertain. The picture we get then is that in every point of spacetime every possible velocity is present, embodied by at least one vacuum particle. This is equal to the Field of all possible velocities that from the beginning was an essential part of the theory of gravitation in this website.
The fermion explosion of vacuum particles gives birth to the field of all possible velocities (2.2)
Originally in my theory of gravitation the Higgs field was a superposition of all possible Higgs fields that each have one specific velocity all over space. It seemed the most logical guess. *a)
However, in one fermion explosion all participating particles are real relative to each other, that's how the fermion demand works. They are not superposed onto each other. In the Heisenberg requirement the different locations are superpositions relative to each other: a measurement of one location makes that location real
while the other locations would vanish
(collapse of the wavefunction). So when fermion and Heisenberg demands are applied together, one gets one fermion explosion in every possible place and when an observation takes place (one Higgs field absorption) only one fermion explosion remains at the specific spacetime point of the Higgs absorption. In other words, not the entire field of one specific velocity would be a Higgs field at the moment of Higgs absorption, but at the location of Higgs field absorption only one entire fermion explosion would remain, while the fermion explosions at all other places would vanish (collaps of the wavefunction). Anyway, the Higgs field absorbing particle still stands still relative to the vacuum, as if being the only point obeying that requirement. At the moment of Higgs field absorption the absorbing particle is the center of the universe at the moment of the BB (the BB of the vacuum particles).
To obey that last expression, at the moment of the BB
, we need another Heisenberg relation:
ΔE * Δt  h/2
h/2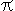 (2.3)
(2.3)
E = energy, t = time, h = constant of Planck
When we fix the energy E of the fermion explosion at 0 (zero) and in doing so determine it for 100 %, then the moment t of the explosion would be 100 % uncertain:
The fermion explosion of vacuum particles can be any moment in time (2.4)
It is a kind of field of all possible expansions (very first state only), where all possible
= ranging all over spacetime
. In (3.2) we will see how the zero-energy requirement is fulfilled.
The field of all possible expansions replaces the field of all possible velocities. (2.5)
These two expressions are equally valid. We will often still talk about the field of all possible velocities, keeping in mind it had originated as the field of all possible expansions.
All this is taking place immediately at the very first moment of the BB, before the first strong force reaction could have taken place. The vacuum particles are spreading itself out all over space and time, making sure also the very first strong force reaction takes place in existing vacuum.
As soon as the fermion exclusion principle could work, the Heisenberg uncertainty relations would work too. So if the vacuum particles have been driven apart by a fermion explosion, then from the very first moment the field of all possible velocities would have been present, instead of the fermion explosion. One very well could say that there never was a fermion explosion of the vacuum particles, although the BB of vacuum particles still can be treated mathematically as a fermion expansion. Compare the previous page of THE EXPANSION OF THE UNIVERSE, the column at the right around the fireworks explosion picture.
 +
+
 +
+

= 
 +
+
 +
+
 +
+
 +
+

Fig. 2.6
In every box are shown the same three locations (red dots). The superposition of three different fermion explosions in three different places, equals the superposition of five fields of one specific velocity. Mark this is only a reordening of velocity vectors over the superposed states, it is no state transition. The locations (red dots) are not displaced and no vectors are displaced, removed or added. As a result an infinite sum of fermion explosions equals an infinite sum of Bose condensates (the fields of one velocity each).
Antimatter vacuum particles
What is the vacuum? According to paragraph The three generations at page 5 of QG (QUATERNION GRAVITATION) each generation has its own Higgs field: the 3rd generation Higgs field consists of pairs of gluons made of 4 colored quarks per pair; the 2nd generation Higgs field is consisting of spin 0 photons that consist of a colorless quark and its colorless antiquark, both with electric charge; and the 1rst generation Higgs field consists of spin 0 neutrinophotons that are equal to a colorless quark antiquark pair without electric charge. (For neutrinophotons see paragraph Neutrinophotons at page 4 of QG.) All fields are supposed to be Bose condensates that are a grid, the solid grid of the vacuum, solid as long as there is no Higgs field absorption from it. (3.1)
We are still regarding the fermion explosion of vacuum particles. We have chosen the BB of the vacuum particles in its ultimate earliest state to consist of identical quarks. How to come from one field of identical quarks to three Higgs field Bose condensates?
In this website the vacuum particles of all three Higgs fields (colored gluon pairs; spin 0 photons; spin 0 neutrinophotons) ultimately consist of a quark and an antiquark within their time borders. The fermion explosion so far provides quarks only.
In this website is chosen that
matter goes forward in time and antimatter goes backward in time
which is (7) and (8) in paragraph Time reversed gravitation at page 2 of THE EXPANSION OF THE UNIVERSE.
There is chosen to follow the scenario as sketched in item 15 at page 1 of THE EXPANSION OF THE UNIVERSE, where at the BB the matter goes forward in time while the antimatter goes backward in time starting from the same BB, in doing so forming an antimatter universe that is completely separated from our universe. Also those antimatter consisted initially of identical antiquarks only. (Antiquarks as we see it. They see quarks, they see themselves as matter and see us as consisting of antimatter).
So in order to get the antiquarks in our vacuum, I have to assume a second fermion explosion in our vacuum right through the first fermion explosion and identical to it, except for that it yields antiquarks instead of quarks.
In the 3rd alinea of paragraph The electron-positron photon Higgs field
at page 5 of NET FORCE IN QED, and tried to work out a little further in paragraph Dark mechanics at page 2 of QG, the mass of a quark and the mass of the identical antiquark (identical except for being anti) cancel each other to precisely zero. So
The quark and antiquark explosions together have precisely energy zero (3.2)
The just described scenario, also following item 15, one may conclude to
( a 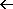 BB1
BB1  a ) + ( a
a ) + ( a 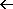 BB2
BB2  a ) = ( a + a
a ) = ( a + a 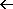 BB1 + BB2
BB1 + BB2  a + a ) (3.3)
a + a ) (3.3)
or conclude to
( a  BB
BB  a ) + ( a
a ) + ( a 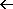 BB
BB 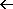 a ) = ( a + a
a ) = ( a + a  BB + BB
BB + BB  a + a ) (3.4)
a + a ) (3.4)
Underlining here means anti-, a = quarks, a = antiquarks; BB1 = Big Bang 1, BB2 = Big Bang 2;  = backward time direction;
= backward time direction;  = forward time direction; BB = Big Bang with before and after the BB only forward time direction, BB = a kind of anti Big Bang with before and after the BB only backward time direction; a = quarks = the whole bunch of identical quarks in the fermion explosion, ditto for a = antiquarks.
= forward time direction; BB = Big Bang with before and after the BB only forward time direction, BB = a kind of anti Big Bang with before and after the BB only backward time direction; a = quarks = the whole bunch of identical quarks in the fermion explosion, ditto for a = antiquarks.
(3.3) and (3.4) are considered to be equal, only the ordering is different. (3.5)
Two fermion explosions give rise to three Higgs fields
How the recombination of a fermion explosion with an anti fermion implosion yields the colored gluon pairs, the spin 0 photons and the spin 0 neutrinophotons of the three Higgs fields? The vacuum quarks and the vacuum antiquarks at the same place in the im/explosion are taken to stand still relative to each other, they can recombine to bosons. However, a recombination process certainly disrupts the fermion explosion and would disrupt any bose condensate as well. (4.1)
Maybe I am making things unnecessary complicated. The vacuum quark fermion explosion and the vacuum antiquark fermion implosion (as they observe it) draw each other. Therefore any quark in the explosion is at the same location as the corresponding antiquark in the implosion. As described at page 5 of NET FORCE IN QED, to form the photon an electron e- and a positron e+ only approach each other until relative distance is too small for the vacuum to distinguish Higgs field absorption by the e+
from Higgs field emission of the e-
(within its time border). See especially paragraph The color of the photon at that page. The e- and e+ within the photon don't react with each other. They don't interchange a particle. They only stay put to each other without seeing each other. *b) But the vacuum does see both of them, one of them emits toward the Higgs field and the other absorbs the same amount of it.
So, in the vacuum fermion explosions, a quark and its corresponding antiquark at the same place don't react either. They don't see each other (although they live in the same world). For the colorless quark-colors +1 and -1 this is described just above. For colored quarks this is in agreement with paragraph Two gluons of opposite sign do not react at page 3 of QG (although this paragraph is way after the black bar that says that, if you are reading TONE for the first time, you can skip the rest of the page).
The quarks don't see each other, but the vacuum does (here you see the necessity of presuming some kind of already present vacuum, isn't it?) and declares them to constitute spin 0 gluons. Or spin 0 photons. Or spin 0 neutrinophotons. We didn't need a state transition to achieve (4.1). The Bose condensates continue to exist.
And here we meet another feature. In the identical fermion explosion all quarks are supposed to have the same spin, otherwise they would not be identical. In the identical fermion implosion all antiquarks have the same spin too, somehow it is the opposite spin as observed from the matter quarks, I guess because of the zero energy requirement (3.2). So when they compose to bosons, the composite spin is 0. But internally there are only spin up quarks (suppose it are spin up quarks) and spin down antiquarks. The very first sign of parity asymetry (There only are observed spin up neutrinos and spin down antineutrinos
). (4.2)
How to proceed? The process described so far creates one vacuum, one Higgs field. Which one, and where are the other two? Does the BB set out as a superposition of fermion explosions of all possible identical quarks? And did we, our universe (which universe? We are still creating our universe), somehow perform a measurement so that we find ourselves back in only one of them, with spin up neutrinos and spin down antineutrinos? Then still remains the question how the other two Higgs fields are formed. Or maybe there is only one Higgs field and are the other two created at the spot when necessary, compare paragraph The spin consideration at page 3 of QG, especially (3.6).
![]() O
O
![]()
![]() NVESTIGATE
NVESTIGATE
Remnant particles in the fermion explosions
To obey the zero energy requirement (3.2) the vacuum particles and the vacuum antiparticles have to match precisely. This holds for the vacuum particles. For the real matter and real antimatter in our universe hold other requirements. This page started with a fermion explosion of matter, see (1.6), then we shifted to the fermion explosion of vacuum particles, derived the field of all possible velocities and found one Higgs field. And now I find myself having difficulties in describing again the matter we started with.
In item 15 at page 1 of THE EXPANSION OF THE UNIVERSE (page 21 of TONE) is said that the matter and antimatter in our universe not necessarily have to match. Page 2 (page 22 of TONE) describes the universe as divided in forward time evolving matter areas and backward time evolving antimatter areas. For this view to become true out of the BB, one expects here at this place extra quarks and there, in other places, extra antiquarks to be added to the two vacuum fermion expansions that draw *c) each other. Locally the counterpart is missing (in the antimatter areas is missing the matter, in the matter areas is missing the antimatter), so the quarks and antiquarks, amongst which are a lot of colored quarks, locally have no other choice than to recombine to baryons or antibaryons. (5.1)
Suppose we presume that the extra quarks and extra antiquarks all have their own fermion explosion, and somehow these fermion explosions don't overlap. *d)
Take an arbitrary point as center where you imagine the BB had taken place. The shown surfaces propagate away from the center and are expanding. h1 is e.g. a bunch of identical quarks, spreading out over surface g1; h2 is a bunch of identical antiquarks, spreading over g2; ditto for all the other bunches that have same velocity (and thus end on the same sphere) but different direction.
A fermion explosion is set immediately, from the very first moment a bunch of identical quarks exists. The strong force has a reaction time of about 10^-23 sec, so during the very first 10^-23 sec there are no strong force reactions, the strong force is unlikely to react earlier than 10^-23 sec after the BB. Moreover, according to paragraph The proton at page 4 of QCD, when the identical quarks (that are going to shape an area) are on precisely the same spot, they don't react with each other by the strong force. The fermion explosion is at least 10^-23 sec free to work. How far can neighboring quarks travel away from each other in 10^-23 sec? That depends on the specific expansion rate. Lightspeed * 10^-23 sec = 3 * 10^8 * 10^-23 = 3 * 10^-15 m = 3 fm, but neighboring quarks are slower than that. What is the minimum expansion rate such that the vacuum can distinguish every particle in the expansion as having a different velocity? At 3 fm the coulomb force is the only significant force between protons. (For protons, mind (34) in Gluon average speed at page 4 of QCD.) Anyway, within the very first 10^-23 sec the quarks in principle are able to reach 0.9 fm mutual distance by fermion explosion. At 0.9 fm the strong force is at maximum. (5.2)
Then in one area quarks unite to baryons, and elsewhere, in other areas, antiquarks unite to antibaryons. *e) Yes, this is a state transition! This disrupts any fermion explosion of remnant particles completely and causes a lot of condendensation heat that will provide an ordinary explosion. Identical quarks *f) can by pairs be converted to other colors, electric charges and spins. In doing so it transforms the remnant vacuum particle part into parts of real particles and real antiparticles.
The BB of matter (sole quarks) and antimatter (sole antiquarks) can in its very first moments be driven by a fermion explosion, but after about 10^-23 sec the BB was driven by the heat of quark recombination, quarks that form baryons and antibaryons. (5.3)

Along with the first strong force reactions are mass absorptions by the quarks from the Higgs field and that causes gravitation according to the mechanism of page 3 of NEG and page 2 of THE EXPANSION OF THE UNIVERSE. Since the just-formed baryons and antibaryons are at a distance of 0.9 fm (strong force at maximum) up to 3 fm (maximum distance traveled), don't they form a black hole then? It is very near to the black hole treshold mass density, so I guess yes, some will, and others won't. (5.4)

Yet still a last remark on the antimatter. How does such an area of antiquarks, observed from us as emerging from the BB, looks like when observed from their own backward time evolving area of space? In their frame they see an implosion towards the BB. Their hadrons exist in an utterly unordered state, caused by a universe's lifetime of reactions. Then, as they observe it, the hadrons spontaneously decouple and form an indentical quark cloud (identical antiquark cloud as we should observe it) that contracts to what they would call a BC, a Big Crunch (fermion implosion).
As observed by us, the cloud of antiquarks (just quarks to them) must be drawn, all antiquarks made being identical in that last moment. But drawn by what? The antiquark cloud is an independent piece of space, there is no need from our BB to demand that they all must be identical.
So maybe they weren't. Then in the BB the quarks are treated a tiny little different than the antiquarks. Quarks might form a fermion explosion until 10^-23 sec had elapsed or mutual distance had reached 0.9 fm. Antiquarks are just an unorderly bunch of antiparticles from the start (that's our BB), or I mean until the end of their universe (at their BC). (5.5)
Drawing is introduced in Observing Dark Galaxies in the column at the right at page 2 of THE EXPANSION OF THE UNIVERSE. Discussion about drawing is not yet settled, see e.g. paragraph The time border and the gluon of color 1 at page 3 of QG. (5.6)
![]() NDER
NDER
![]() LONG TERM
LONG TERM
![]() ONSTRUCTION , I guess
ONSTRUCTION , I guess
--- A previous attempt ---
The moment of recombination of the identical quarks with the identical antiquarks might be the moment of highest energy, when the 3rd Higgs field is formed first. (The Higgs field of the 3rd generation gives the highest masses to real particles, so it must be the most energetic field of the three.) Further expansion cools the 3rd Higgs field until it doesn't have enough energy left to sustain the 3rd generation particles and falls to the 2nd Higgs field made of spin 0 photons that are made of colorless quarks with electric charge.
But mind, there not really is a fermion explosion of the vacuum particles, there immediately is the field of all possible velocities in which there is no further evolution, isn't it? So there is no such thing as cooling down either in the vacuum particle field. All three Higgs fields must be there from the very first moment, the moment of recombination of the quarks with the antiquarks.
So we should regard Higgs field 3 first.
According to (2.8) and (2.10) in paragraph Building vacuum from gluons at page 2 of QG, the gluon pairs of the vacuum are the superposition
( i -i ), ( j -j ), ( k -k ), ( 1 1 )
while the gluon pair superposition of the backward time evolving areas of vacuum is
( i -i ), ( j -j ), ( k -k ), ( -1 -1 )
At several places in this website is concluded that areas of forward time evolving vacuum and areas of backward time evolving vacuum can spatially exist next to each other, separated by the time border. And how to proceed then?
--- End of previous attempt ---
Matter
Let's return to the matter that expanded from the BB. No superpositions here, all particles are real. The expansion cannot be converted into a field of all possible velocities by means of velocity vector reordening.
For the real matter that the BB consists of, we continue (1.4) The bunch of particles the BB consists of, very well might have been identical quarks only
, and (1.6), The BB is driven by an identical-fermion explosion
.
The CMB (cosmic microwave background) is generally accepted as the remnant of the BB and originated at 400,000 years after the BB. The nowadays temperature of the CMB has been measured to be the same in all directions, to about one part in 100,000. This gives rise to the so-called horizon problem. Is the precision of the identical-fermion explosion sufficient to explain the isotropy deviation of no more than one part in 100,000 and thus solve the horizon problem?
![]() O
O
![]()
![]() NVESTIGATE
NVESTIGATE
The velocity of the universe is determined then about 100 % everywhere. So the location of the universe must be indefinite, 100 percent undetermined, in accordance with the Heisenberg uncertainty principle (2.1). Our matter is able to stand still with respect to the expanding frame, more or less embodied by the receding galaxies and especially the CMB.
In our universe as it is now, there is no preferred location where the BB occurred, all locations are equally valid (6.1)
Moreover, as is said just above (2.3): At the moment of Higgs field absorption each particle is the center of the universe at the moment of the BB (the BB of the vacuum particles).
SR still holds. To start with, the model of the expanding universe might be that of Milne: a uniform, isotropic, homogeneous and constant expansion - the uttermost simple expansion there is - of an empty universe, wherein SR is taken into account. Added to the model of Milne are decelerations of the expansion due to gravity in the forward time evolving areas and, in this website only, accelerations of the expansion (as we observe them) in backward time evolving areas.
That the antimatter from the BB has gone backwards in time, starting at the moment of the BB, is a perfect explanation why there is no antimatter in our universe and where it has gone to (6.2)
However, as described in the previous page of THE EXPANSION OF THE UNIVERSE and in item 15 at page 1 of THE EXPANSION OF THE UNIVERSE, there might be antimatter in our universe coming to us along the timeline from another BB in our far future. The amounts of matter we observe around us and antimatter (that we don't see, see item 12 at page 1 of THE EXPANSION OF THE UNIVERSE) then don't have to match. In this website there is a preference for the existence of these foreign antimatter and the foreign antimatter is regarded as the cause of the acceleration of the expansion of the universe. See also paragraph The beginning of the Universe - a previous attempt at the previous page of the storyline THE EXPANSION OF THE UNIVERSE.
Paragraph The proton at page 4 of QCD chooses the strong force between quarks and gluons to be at maximum at 0.9 fm mutual distance and for shorter distances to be proportional to distance and zero at zero distance. So at the very first instant of the BB, when all identical quarks coincide, the strong nuclear force yielded no contribution. Only the electromagnetic force can have worked at the very first instant. (6.3)
However, the reaction time of the electromagnetic force is at least 10^-20 sec. So at the very first instant of the BB the electromagnetic force yielded virtually no contribution too, because the electromagnetic force is too slow to have achieved significant events by then. (6.4)
I am not sure about the implication of (5.3) that the strong force has to wait until neighbouring quarks in the fermion explosion had approached 0.9 fm and 10^-23 sec had elapsed. It appears to me that as soon as the universe has some extend, the strong force from a certain quark would pass over the nearest neighbor quarks and reach for the quarks that are at 0.9 fm distance. The structure of the universe then resembles a bit that of the rings of a chainmail that the medieval knights used to wear instead of the nowadays bulletproof vest. (6.5)
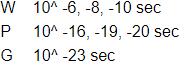 (6.6)
(6.6)
W = Weak force; P = Photon, the electromagnetic force; G = Gluon, the strong force.
We take this as the reaction times of the forces. The lifetime of an unstable particle determines with nearly absolute certainty under which force it decays.
CMB
The decoupling of matter and radiation at 3000 K, about 400,000 years after the BB, was the moment of birth of the CMB that then equals a black body radiation of 3000 K. Since then the matter has clumped into stars, galaxies and clusters of galaxies. The CMB temperature still is isotropic to about one part in 100,000. So the evolution has had no influence on the 2.7 K isotropy. So we may conclude that also the supposed dark antimatter galaxies would have had no influence on the 2.7 K isotropy. (7.1)
The observed temperature of the CMB now is 2.7 K, more than 1000 times smaller than 3000 K. The accepted explanation for this is that the wavelengths of the CMB radiation are stretched in the course of time, they arrive stretching. (7.2)
Here I would propose a simpler explanation. At 400,000 years ATB (After The Bang) our location (the location that will become us) received 3000 K radiation from the direct neighbourhood. That radiation has passed us by since. One billion years later we receive the CMB radiation from locations one billion lightyears away. Those locations recede from us and the light from those locations is severely red shifted to a much lower temperature than 3000 K. Also that radiation has passed us by. Another 12 or 13 billion years later - we are in present times now, 13.8 billion years ATB - all those radiations has passed us by and we are receiving now radiation from places about 13.8 billion ly away. Those places recede that much that the CMB has red shifted to the nowadays observed 2.7 K. It resembles a bit the reasoning in the solution for the paradox of Olbers that I found, see page 7 of the storyline THE EXPANSION OF THE UNIVERSE.
The CMB that we observe is cooling down in the course of the billions of years (7.3)
Which is the same conclusion as the accepted one in (7.2).
![]()
Just another possibility for CMB-like radiation.
During acceleration the accelerated matter experiences the surrounding vacuum as having a temperature proportional to the acceleration (Davies-Unruh equation) (7.4)
This is supposed to hold in forward matter areas as well as in backward antimatter areas.