We sketch an outline of the vacuum and gravity
Three Earth’s diameters above the Earth’s surface there are four little blocks, standing still relative to the Earth, and the stars. (Of course this is impossible. The stars of our galaxy all have some motion relative to each other, the sun is just one of them, the Earth moves around the sun and around its axis. But for convenience we take all these velocities to be zero.) The masses stand still with respect to the vacuum around them. Then the blocks start to fall under the force of gravity.
The vacuum starts to stream and drags along with it all masses that are floating in it. The dragging is 100 percent, the floating masses keep standing still with respect to the streaming vacuum. All masses float side by side, they all fall with the same acceleration. They don’t feel the dragging. They are free floating and weightless. As if there is no gravitation. As if they are standing still.
This supports the view that the floating masses are NOT reacting with the gravitational field. Instead they avoid reaction with the streaming substance of the vacuum
. The masses don’t couple to the gravitational field. They go with the gravitational stream to avoid the need of a coupling.
When a mass finally hits the Earth surface, it lies motionless there, resisting entirely the dragging force of the vacuum into the Earth. (Most objects will shatter, fall apart, bounce and so on. We take all these effects to be zero for our idealized blocks.) The force of the mass onto the sustaining surface is the weigth. Is the mass then reacting with the vacuum?
There is the Davies-Unruh effect stating an object that is accelerated in free space will undergo a very tiny temperature increase proportional to the acceleration. The Davies-Unruh effect occurs because the particles of the object react with the particles that according to the relations of Heisenberg continuously are popping in and out of the vacuum. As far as I know, the Davies-Unruh effect is not yet experimentally confirmed. Gravity and acceleration are indistinguishable and thus objects lying on the surface of the Earth are expected to undergo this temperature increase too.
So, if the effect exists, the vacuum is coupling to the masses lying on the ground.
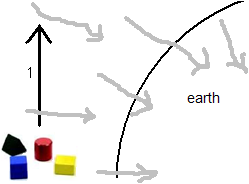
Fig. 4
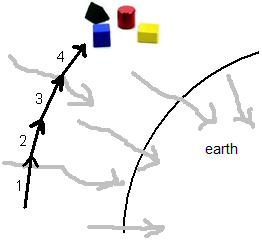
Fig. 5
Fig 4. Now we start with our four little objects to move with rectilinear constant speed perpendicular to the Earth radius (arrow 1). The stream of the gravitational field (grey arrows), perpendicular to arrow 1, drags the objects along with it, towards the Earth. The two perpendicular velocities add to arrow 2 in fig. 5.
Fig 5. The objects once again stream with rectilinear constant speed (arrow 2). Again the stream of gravity drags along the velocity of the objects towards the Earth. The velocities add and result in the slightly deviated velocity of arrow 3. And so on. This make the objects to follow a curved path around the Earth. We assume the objects to have a velocity with respect to the vacuum.
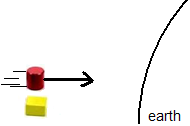 Fig.6
Fig.6
Fig.6. The yellow block is standing still with respect to the Earth and has just started to fall. At that moment, very nearby, a red block passes by. It is falling to the Earth too but it had started earlier, higher above the Earth.
Up until now we assumed a particle can have a velocity with respect to its surrounding vacuum. That is, without reacting with it. The object with its velocity is dragged.
1) In figure 4 and 5 we assumed a vacuum that drags the blocks with it. The velocity of the blocks is more or less perpendicular to the dragging direction of the vacuum.
2) It is an experimentally known fact that, when two objects with relative speed like the blocks in fig. 6, are falling in a gravitational field, they will maintain this relative speed while falling. A small velocity increment dv will be maintained while taken along with the fall in the gravitational field.
3) A lorentz invariant field of all possible velocities will entirely be dragged by the Earth gravitation.
4) In page 6 of this storyline we assumed a particle has a velocity that places it outside its homebase
. A velocity is taken along with the expansion of the universe, without changing magnitude.
The area of space lined out by the blocks, drags along everything in it, every block as well as every speed they have. A small amount of dragging adds to each velocity the same velocity increment. Then in fig. 6, there is no need for an extra, fast-falling vacuum, in which the red block stands still. Nevertheless, such an extra vacuum does exist in the field of all possible velocities.
The entire assemblage of all possible speeds is dragged by, and not only one of them, or four of them, when all four blocks have different speeds.
(If so then those one up to four velocities would have passed to another velocity, merging with it and thus disappearing. And leaving an empty velocity in the invariant field of all possible velocities. It would no longer be invariant.)
Next page we will see one better regard this situation as a vacuum that moves along with the blocks and with respect to which the blocks stand still. That vacuum has a velocity parallel to the Earth surface and perpendicular to the dragging direction of the vacuum that sags into the Earth. The vacuum that drags the blocks towards the Earth instead drags the vacuum that is comoving with the blocks.
A sphere of free falling clocks
When a large intergalactic sphere of free-falling clocks expands due to the expansion of the universe, it expands uniform. After expansion it is still a sphere. When a small sphere, e.g. 1 km diameter, of free-falling clocks is released in the gravitational field of the Earth, e.g. 10,000 km above the Earth surface, it will deform. This deformation is not a pure contraction. When falling towards the Earth, the sphere contracts parallel to the Earth surface, but perpendicular, along the straight line to the Earth’s gravitational centre, it will stretch. The stretching is because the front side of the sphere is a little bit nearer to the Earth’s gravitational centre than the rear side and thus will feel a little stronger attraction to the Earth - and this will maintain to be the case during the rest of the fall onto the Earth surface. What happens then, below the surface, depends on the content. Suppose the deformed sphere of clocks just continue its fall.
Leading thread is the theorem of Gauss. Suppose you have a sphere that consists of spherical shells of same composition and thickness all over each shell. Nearly all planets and stars obey this, more or less. Then all shells above
you (you are inside the shells) can be neglected; all gravitational influences cancel out precisely. The mass of all shells below
you (you are outside the shells now) can be considered to be concentrated in the gravitational centre.
When there are no shells below you (the sphere is hollow) you will be weightless there. You stand on the inner surface of the shells but you have no weight at all due to the mass of the shells.
GR
GR - General Relativity - says ALL possible frames are permitted as frame of reference. Imagine an air force stunt team made a perfect threedimensional rectilinear grid in the atmosphere. The grid is made of smoke trails. All grid lines are provided by a neat scale indent division. Then strange winds stretch and curl this part of the grid, displace and rotate other parts, make shrink and whirl still other parts, and so on. The only demand is no line is disrupted. Define the three laws of Newton with respect to THIS frame. Pacing at constant rectilinear velocity means you keep traversing along such a distorted smoke grid line, all the time making sure to pass the same amount of smoke scale indents per unit of time. No matter how curved the line is or how irregular the scale indents division has become or still do vary in time. And all forces one feels when performing such an enforced constant velocity along a straight line are called gravitations. This is Newton's first law in action. This is, in brief, the point of view of GR.
A permitted frame in GR is the frame of free-falling clocks in the gravitational field, the frame that falls along with gravitation and in which there is no gravitation no more. The frame of clocks that is free-falling along with the accelerated expanding universe is another such a frame too.
Another permitted frame is the Earth, the molecules of the Earth. Or the background euclid grid of vacuum particles, see page 3 of this storyline.
Masses fall weightless in each other's gravitational field, as if there is no gravitation. No gravitational force acts on any mass; no mass goes anywhere caused by a gravitational force.