O
NVESTIGATE
This pop-up frame calculates the relative distance of the marbles the vacuum *) consists of. This distance is calculated about 10^-21 m.
*) I now consider the vacuum to consist of 3 Higgs fields, three different vacuums in fact, see page 5 of QG. THE vacuum is taken as the strongest one of them, the 3rd Higgs field. While we, ordinary people, absorb mass from the 1rst Higgs field.
November 2023
O
NVESTIGATE
Length in meter m, surfaces in square meters, time in second s, mass in kilogram kg,
acceleration at earth's surface = 9.81 m/s^2
Surface of sphere = 4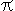
r^2 = 2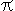r * 2r = circumference * diameter
Earth surface = (4 * 10^7) * (1.28 * 10^7)
Volume of spherical shell that sags into the Earth every second
= Earth surface * thickness shell
= Earth surface * 1/2 * 9.81 * t^2, where time t = 1 s
= Earth surface * 9.81 / 2
= (4 * 1.28 * 9.81 / 2) * 10^(7 + 7)
mass of the earth = 5.97 * 10^24 kg = (5.97 / 1.67) * 10^(24 + 27) protonmasses.
This is the number of nucleons the earth consists of.
We regard all neutrons in the earth as protons and we skip all electrons. The mass difference between the neutrons and protons increased with the mass of all electrons is supposed to be (more than) canceled out by the mass defect of all those nuclei.
Each nucleon consists of 3 quarks. Each quark reacts 10^23 times per second via the strong nuclear force (gluon couplings). Per reaction we assume two vacuum marbles to be absorbed.
The number of reactions per second for electromagnetism (charge-photon couplings) is at least 1000 times smaller, so we skip all photon couplings and their associated Higgs field absorbtions.
Mark the electron mass is roughly about 1000 times smaller than the quark mass.
The number of vacuum particles (Higgs or gravitons, which are assumed to be of equal volume) absorbed per second in the earth =
(2 * 3 * 5.97 / 1.67) * 10^(24 + 27 + 23)
The volume of one vacuum marble then is the volume of the shell divided by the number of particles absorbed per second.
Volume vacuum marble = (4 * 1.28 * 9.81 * 1.67) / (2 * 2 * 3 * 5.97) * 10^(7 + 7 - 24 - 27 - 23) =
1.17 * 10^-60 = (1.05 * 10^-20)^3; that is a cube with sides of 1.05 * 10^-20 m or a sphere of radius between 10^-20 and 10^-21 meters.
So along a proton diameter - a little smaller than 10^-15 meter - fit about 100,000 up to a million vacuum marbles.
Volume of spherical shell that sags into the earth every second / mass of the earth =
= (4 * 1.28 * 9.81) / (2 * 5.97) * 10^(7 + 7 - 24)
= 4.21 * 10^-10 m^3 / kg 
4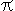/3 * 10^-10
So if per sec per kg there disappears a volume of about 10^-10 times the volume of a sphere of radius 1 m and the vacuum drags along with it all objects in it, then there is simulated a force between masses of
F = 6.67 * 10^-11 * (mass 1) * (mass 2) / distance^2