Definition by construction
Let's define the field of all possible velocities by creating it. For convenience, situate yourself free floating in empty space. Take a sufficient small part of space to work in so that curvature is negligible. Define yourself as standing still. Choose a straight line L through your location. Lay down a long row of blocks standing still to you along L - anyway, if not endless, make it as long as possible. This is row 1. Choose a lowest velocity increment dv, e.g. one quark diameter per million years in 1 of the 2 possible directions along L. Increase your velocity with one dv. You move now with constant speed along row 1. In this new state, define yourself as standing still. Lay down another long row of blocks along L standing still to you; this is row 2. Then again increase your velocity with one dv. Again define yourself as standing still and lay down a long row of blocks - row 3 - along L standing still to you. The velocity of row 2 relative to you is -dv but the velocity of row 1 relative to you now is (-dv -dv) / (1 + -dv * -dv / c
), according to special relativity. And so on, up to an infinite repetition in both directions along L (or anyway parallel to L). Repeat the whole procedure for all possible directions L can point at. Now there is one row of blocks comoving with each possible velocity. You have made the field of all possible velocities.
Changing velocity then is the same as jumping to another row of blocks. To whatever velocity you change, you always find one row of blocks standing still to you and the wide array of rows of blocks with different speeds around you will always look the same, by virtue of the specific way we created it. So this field of all possible velocities exists, is velocity invariant and is Lorentz invariant too. It has to be, there is just no other way, due to the specific way we created it.
Compare an endless stairs of identical steps, each step one foot wide and one foot high. You stand on one step. Due to ordinary perspective you see steps smaller when further away from you. The steps loose dimension in the distance, in both directions of the stairs. Now imagine every step corresponds to a velocity. The step you're standing on corresponds to standing still and two subsequent steps differ one dv. The stairs now is the set of all possible velocities along one line L. Identify the visual reduction of each step with the precise SR-caused velocity decrement of the velocity of the corresponding step. Raising (or descending) one step doesn't change the appearance of the stairs; you will not notice any difference. Every step will adopt the precise velocity decrement of its nearer neighbor when one step nearer. And of its further neighbor when one step further away. When raising or descending the stairs, the set of all possible steps remains the set of all possible steps.
If you choose to use a finer grid of velocities, e.g. 1/10 dv, and start the procedure, then after 10 increments you don't end up at precisely one dv total increment, but a tiny little bit slower, because of the mentioned special relativistic summing of speeds. The finer grid is a better approximation, so you can't use any part of the old grid any more. You have to do it all over again, all the steps of creating the field of all possible velocities. So you better choose dv from the beginning small enough for all your purposes.
In doing so, reaching up to infinite small dv, the impulse of the blocks becomes more and more definite and the blocks spread out all over space (uncertainty relation). This saves us, construction workers, the effort to repeat the whole procedure for every point in space. We could do with one block per row. (I wonder if one row of blocks isn't just one element of the wavefunction, see page 1 of the storyline GRAVITATION).
(1)
(2)
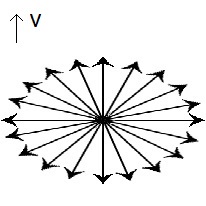
Regard the field of velocities of one single velocity magnitude in all directions (1). (We depicted a plane only, but imagine it to be a sphere of velocities.) When one is speeding by this field with velocity v, the field is Lorentz contracted (2). Blocks in the direction of v will be nearer to each other, while blocks in the direction perpendicular to v will not be affected. As an overall result the block density will increase. If each block had a tiny mass, the field would become more massive. The field is stronger.
Pages using the field of all possible velocities
page 2 of DIMENSIONS
An infinite number of superposing vacuums is not new, they are a necessary ingredient in the field of all possible velocities, a concept that is needed more than once in TONE, my Theory Of Nearly Everything. (TONE is accessible from the upper part of the Contents. And nr 9 in the Additions line of the small contents below in nearly every page. The Contents is accessible by clicking the black dot that always is above and below each page.) To be sure, each of the superposed vacuums (two in this case) consists of its own field of all possible velocities. This is no problem: the fields are Lorentz invariant, one can add one on top of the other and the resulting field will not show a change.
Renormalization Argument 1 at page 4 of THE COLLAPSE OF THE WAVEFUNCTION
In QED renormalization procedure, in each Feynman diagram the amplitude is reciprocal to r, where r is covered distance. The paths of the infinite split-off immoral electrons lay in spacetime, so they have a definite shape in our universe. So for the renormalization procedure of QED itself it is important whether the routes traversed in each contribution, in each Feynman diagram, are dragged along in the action of gravity as described in the NEG storyline. Or that the traversing is to be taken through flat spacetime, the paths being superposed to all gravitational activity, existing in its own empty flat vacuum where in thought all particles that are not needed, are erased. Mind in NEG the Higgs field absorption is taken from one single field out of the field of all possible vecocities.
page 5 of NET FORCE IN QED
Both the gluon sea as well as the e- e+ sea are supposed to exist as fields of all possible velocities. When one field is going to get in motion relative to the other, nothing will change since both fields are velocity invariant and special relativistic invariant.
The Globular Cluster at page 5 of THE EXPANSION OF THE UNIVERSE
When disordered motion, as in globular star clusters, is transformed into an ordered expansion by translocating stars, keeping their impulse vector lengths and directions the same, the result looks like a fireworks expansion. In a fireworks expansion as it is meant here, the velocity of one piece of firework is proportional to the distance to the expansion center. It looks very much like the expanding universe described above. Each possible velocity has its unique proper place. This space then is a version of the set of all possible velocities.
The Big Bang at page 4 of THE EXPANSION OF THE UNIVERSE
The fermion explosion of vacuum particles gives birth to the field of all possible velocities (2.1)
Summary for an accel expand univ at page 5 of THE EXPANSION OF THE UNIVERSE
Especially a small velocity increment dv will be maintained while taken along with the expansion and so a lorentz invariant field of all possible velocities can be constructed in the expanding space of the universe too.
page 1 of NEWTON EINSTEIN GRAVITATION
3) A lorentz invariant field of all possible velocities will entirely be dragged by the Earth gravitation.
page 3 of NEWTON EINSTEIN GRAVITATION
When at motion with respect to such a marble field, because of the Lorentz contraction the field will become denser. To be Lorentz invariant like the vacuum is, the field has to be the superposition of the vacuum particle fields of every possible velocity, the superposition of all grids of solid marbles that only differ a velocity, pervading each other without seeing each other. The solid marble oceans pervade the Earth too. In fact all of Earth, i.g. all matter, is just another superposition to the fields. It is very much like the field of all possible velocities.
page 5 of NEWTON EINSTEIN GRAVITATION
There is no space behind the space (except for the rest of the field of all possible velocities that superposes the specific Higgs field from which is absorbed from), so it can be there is no
hole particle
to observe there.
page 6 of NEWTON EINSTEIN GRAVITATION
It is this decision that defines the empty spot mentioned at page 3 of NEG. Mind there is no space behind the space, except for the field of all possible velocities.
page 8 of NEWTON EINSTEIN GRAVITATION
Normally a field will Lorentz contract and therefore become denser when moving faster relative to it. But when all possible velocities are present and then one moves with respect to it, then your velocity will be added to every of the possible velocities and nothing will change. The field is still the field of all possible velocities. The Higgs field is
velocity invariant.
page 5 of QQD
Any particle only absorbs from that vacuum, that Higgs field, with respect to which it is standing still. Only then it absorbs the least amount of mass from the Higgs field. Or energy, according to E=mc
. This is in the spirit of page 1 of NEG, where is suggested one can stand still with respect to the vacuum. Still there is no preferred vacuum since there is the superposition of all possible Higgs fields, see page 3 of NEG. For any speed in the field of all possible vecocities there is a Higgs field of that speed, to which you can stand still.
page 6 of QUATERNION GRAVITATION
It can be absorbed by the vacuum, causing a single short and tiny expansion of space. The glueball pushes the present vacuum marbles aside to create enough space for itself to fit in. There always is a vacuum in the superposition of all possible vacuums (vacuums of all possible velocities) with respect to which the glueball is standing still. There it is absorbed in, in the frame of the glueball reducing the field of all possible velocities to this only field. After absorption-and-tiny-expansion all vacuums of different velocity are indistinguishable again and the superposition of all possible velocities is restored, as observed from Outside Observers like us.
Interaction between hadron and lepton Higgs field at page 7 of QUATERNION GRAVITATION
Is there interaction between the leptonic and gluonic Higgs fields? Both fields are fields of all possible velocities, see previous page.
page 8 of SPECIAL RELATIVITY
And I wonder what force that is. Is it a particle, the photon, arriving at the local environment, locally making a choice out of a heap of superpositions? That choice, is that the kind of vacuum particles that surround you? The choice of Higgs field out of the field of all possible velocities? The idea is the Higgs field from which mass is absorbed stands still with respect to the absorbing particle. So far so good, but still unexplained remains why the x- and t-axes would tilt then. They do such that c remains 3 * 10^8 m/s. But why? Just an extra difference to make frames that only differ a velocity distinguishable?
End of The field of all possible velocities
.