In QCD color is a real property. In QCD, despite all attempts so far have failed, it is not forbidden to observe color. In this storyline we replace colors by the imaginary units of quaternions. Maybe a better name then would be QQD, Quantum Quaternion Dynamics, instead of QCD. The units are imaginary and cannot be observed directly as for example the electric charge can.

Colors as imaginary quaternion units

Quaternions are governed by

i = j = k = ijk = -1 (Hamilton 1843) (1.1)

Complex numbers have 1 imaginary axis and 1 real axis. Quaternions have 3 imaginary axes, their units called i, j and k, and 1 real axis, spanning a 4 dimensional world. For a basic summary of quaternions, see pop-up frame Quaternions.

Mark (1.1) also could have been defined as

-i = -j = -k = kji = 1, this is precisely the same. (1.2)

A very nice way to get acquainted to quaternions is the piece of Vincert van der Noort Why the four-dimensional space is the most beautiful of all spaces: quaternions.

In accepted QCD is chosen as colorcharges red , green and blue

These are the three colors of the strong force and together they form something that has no color no more and that is called white.

+ + = white, that is: no color anymore. (1.3)

As anticolors is taken cyan , magenta and yellow

These are the anticolors of the strong force and together they too form something that has no color anymore and that too is called white.

+ + = white, that is: no color anymore. (1.4)

So far the colors and anticolors as they are treated in accepted QCD.

Compare page 1 of the QCD storyline.

There are three imaginary quaternion units and multiplied together they form something that has no imaginarity any more: ijk = -1 or kji = 1. This, together with (1.3) and (1.4), inspired me to the following replacements.

Replace	red	by	i
	green		j
	blue		k
	white		1	(1.5)

Equation (1.2) now becomes:

kji = * * = = 1 (1.6)

Mark that when we had multiplied ijk the outcome would have been -1. We will come back to that later.

With the 6 colors from (1.3) and (1.4) one can construct the color circle. One can imagine a kind of seventh color white in the center. In the colorcircle a color and its anticolor are always at opposite sites of the circle.

(1.7)

From (1.5) and the colorcircle we replace the anticolors.

Replace	cyan	by	-i
	magenta		-j
	yellow		-k
	black		-1	(1.8)

An equation like (1.6) is:

-k * -j * -i = * * = = -1 (1.9)

Mark that when we had multiplied -i * -j * -k the outcome would have been +1. We will come back to that later too.

It still can happen we talk about colors and depict them as a color, pretending this world isn't colorless. But we know now it are no colors anymore, it are quaternion units.

A color and the corresponding anticolor together gives something that has no color no more.

* =

* = (1.10)

An imaginary quaternion unit multiplied by the corresponding opposite unit gives something that no longer is imaginary:

i * -i = 1, j * -j = 1, k * -k = 1. (1.11)

Instead of the colorcircle we now use the axes system of the imaginary quaternion units.

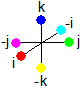
(1.12)

In this picture the angle of projection of the chosen 3-dimensional axes system of imaginary quaternion units is such that the projection resembles the color circle a lot. The fourth axis
1 ------- -1 is not shown.

In QQD there are now 8 gluons (1, i, j, k, -1, -i, -j, -k or , , , , , , , ) from which two of them are colorless (1 and -1) just as in the old well accepted QCD.

Gluons when colors are replaced by quaternions

In QQD Feynman diagrams will be used as is usual in QCD, for example:

The equation of this diagram is:

Q(A B) * g * Q(B C) * GL(B D) (2.1)

(the equation number being ahead is not a mistake)

Put in words this is the displacement of the quark Q from point A to point B times the coupling constant of the color interaction g times the displacement of the quark from B to C times the displacement of the gluon GL from B to D.

In equation (2.1) its composing actions, like Q(A B) and g, are used as a factor. With color we do the same and use color as a factor in the equation.

At point B the magenta quark emits a gluon. The gluon takes away the magenta from the quark and carries it off in its upper color. Taking away normally is a kind of subtraction, but in equation (2.1) you can see that applying an action is multiply in the equation. So here taking away is dividing by magenta .

Taking away magenta = / = / -j = * -( -j ) = * j (1.13)

Then, near to point B, a correlated pair of colors cyan-anticyan appears, a cyan-red pair that is, see the colorcircle. The cyan is given to the quark to replace the taken-away magenta. Giving is a kind of adding, which is a multiplication in the equation.

Adding cyan = * = * -i (1.14)

The remaining red is dragged away in the lower part of the gluon. In accepted color stream representation of QCD that red is depicted as its anticolor cyan.

The magenta goes forward in time, from A to B, from B to D and from D to F. The cyan goes forward in time from E to D and from B to C. But from D to B, following accepted color stream representation, the cyan goes backward in time. When a color goes backward in time it changes into its anticolor, red that is in this case, obviously. See the column at the right.

The gluon now has the potential to add a magenta to an encountering quark (gluon's upper color) and to remove a cyan from it (the gluon's lower color). The potential to remove cyan is the same as the potential to add a red.

Dividing by cyan = / = / -i = * i = *

The gluon then is

= * / = * -j / -i = * i * -j = * *

When dividing a color like -j by another color like -i, it is the same as -j multiplying by i. But mind, you have to left-multiply -j by i. (1.15)

The notation * / = * -j / -i comes closest to depicting gluons as upper and lower color in time-symmetric representation (which we prefer), . Magenta in the upper color, cyan as lower color and the border between them as the breakline.

The notation * * = * i * -j comes closest to the normal representation, .

Other equalities follow:

= / = -j / -i = j / i = / =

which can be checked out in the gluon table.

(In this we recognize the statement/conjecture So we can forget about the colors of the gluon and use its color-shift only in page 3 of the storyline QCD, just above the paragraph Identifying gluons of the same color-shift. But mind, colorshift is abandoned. It's quaternions only now.)

Suppose we would state

= * i * -j = * -j * i = * i / j = * / , which is the opposite from * / .

The first gluon goes from a red quark to a green quark, while the latter gluon goes from a green quark to a red quark. Quaternions usually don't allow a swap of multiplication order, quaternion multiplication is not commutative. The bold = is wrong.

In both cases the red quark and the green quark swap color, the difference is only in the time order of gluon emission and gluon absorption. Which suggests reversing multiplication order is reversing time order - well, at least in this case.

= / = -j / -i = i * -j = -k =

A gluon color pair can be converted to a single color, see the quaternion gluon table.

Only quarks have single color. Quarks have spin 1/2, mass maybe about 20 MeV and charge is +2/3 for the u-quark, or -1/3 for the d-quark. Gluons have spin 1, no mass and no charge. So the transition from a single-color quark into a double-color gluon is not possible until the differences are settled somehow. But no one has ever observed a color, in doing so determining it. Colors remain virtual. So in the superpositions gluons might be considered as single colors, and so we do.

We treat color reactions as if there is a conservation law of color. In fact there is the urge for white end state which says the color sum is a constant and the constant is zero. (1.16)