Colorshift is abandoned now, this is a previous attempt. Quotes from deleted pages.

More possibilities

...3 gluons emitted simultaneously. We can allow 1 quark to emit 2 gluons or all 3 gluons. Simultaneously, or one after the other. We can allow 1 gluon to be emitted that subsequently emits a 2nd gluon. Or that 1rst gluon emits the 2 other gluons. Simultaneously, or one after the other. Or a gluon emits a gluon that emits a gluon.

...A gluon might be a glueball. A glueball can be absorbed by the 1 or 2 remaining gluons, if there are any. Two glueball’s can absorb each other, reducing the number of glueballs present by 1.

...Applying a full turn along the color circle is like circumventing a real lake by walking. When having circumvented the lake for 1/3 of its contour, you arrive at a point. When circumventing the other direction for the other 2/3 of the contour you end up at the same spot, having applied twice the energy you needed for the 1/3 tour. Is it the same for gluons? Applying a colorshift of 1/3 ends up at the same color state as the application of a colorshift -2/3 times a full turn along the colorcircle. If so then the -2/3 colorshift cost twice the energy of the 1/3 colorshift.

 
Color as the phase of a wavefunction

Imagine the color is the phase of a wavefunction. If a full turn around the colorcircle is precisely one wave    then each color is 1/3 of    which yields unequal waveparts. The colors would no longer be fundamentally equal. Likewise with one circle of 2 waves    divided in 3. It is the best to regard one full turn around the colorcircle as precisely 3 waves and each color as one wave

               

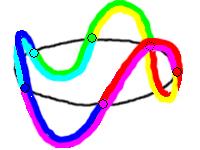
If the wave of a color is then the wave of an anticolor is . One anticolorwave consists of the second half of the previous colorwave and the first half of the next colorwave in the colorcircle. When a color starts with a crest followed by a trough then an anticolor start with a trough followed by a crest. That provides a way to always distinguish a color from an anticolor.

If a color should be an arbitrary 1/3 of the colorcircle (...) So a colorwave always has to start at zero, then going to one maximum, back to zero and going to the opposite maximum and finally ending at zero.

One can arbitrary choose to divide the circle in 3 colorwaves or in 3 anticolorwaves or even in 6 halfcolorwaves. There is not really a difference between particle and antiparticle then.

This leads nowhere. The color is not the phase of a wavefunction.
 

Do gluons really orbit each other?

Gluons move at lightspeed. There is no experimental evidence at all about the velocity of the gluons.

In a glu2on, if the two gluons really orbit each other and still really move about with the speed of light, they might encounter black-hole-like properties.

Gravity curves spacetime up until the event horizon of a black hole. Still larger curvatures lay behind the horizon, impossible for us to see. A ray of light is kept in circular orbit around a black hole at a distance of 3/2 times the radius of the event horizon, although it is an unstable orbit. So when two gluons orbit each other at one and a half times their event horizons, this is physically difficult but not impossible. One has to prove the gluon has an event horizon.
 

The propagation of the virtual gluon

What happens when a emits a that is absorbed by a ? There are at least 4 ways to interpret this.

1) The gluon seems to know on forehand what is the color of the quark it will go to. At its origin the gluon knows its destination in its lower color, which is looking into the future.

When the gluon knows the color of its destination it knows about the spin of the destination too. And the precise direction of emission in space needed for an encounter to take place. When the spin doesn’t fit or the direction isn’t right or whatever-may-be-demanded-further is not satisfied, the gluon is not emitted.

2) The gluon doesn’t know its destination on forehand. It only knows the quark at its origin and bears the origin-quark’s old color in its upper color and the origin-quark’s new color in its lower color (in so-called time-symmetric representation). It just sets off as a gluon that is meant to couple with a cyan quark. It boldly goes where no gluon had gone before, intending just to roam around until it has found its cyan destination. There always is one in an antibaryon.

3) Colorshift interpretation. It doesn’t matter what its destination is. Only the color-shift counts. A can absorb a +shift . But when this leads to a colored end state nature will take measures. Instead of 8 independent gluon fields we need 6.

...It is as if 6 starting quark states (3 colors, each in spin +1/2 and spin -1/2) had emitted 6 gluons, turning the quarks into 6 end states, suggesting 6 superposed worlds in each of which 1 quark emits 1 gluon that ends in 1 other quark. But this isn’t the case at all. The respective identical states that merge, and where the 6 particles do originate from, do not belong to the same worlds. By example the group of 3 number-one end states (see table, not shown) doesn’t match with any group of 3 identical start states. And any group of 3 identical gluon states doesn’t match with any group identical quark start states or end states. So 6 quark states did emit 6 gluon states which turned the emitting quark in 6 end states. But this cannot be separated in 6 independent worlds.

Reactions like these count with the same importance.

 
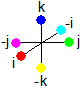
... * = ( -j / -i ) * ( -j /-i ) = i * -j * i * -j = -k * -k = -1

This is a colorless mesonic gluon, part of the time axis.
The solution looks different from those obtained with the colorcircle.
 

Gluon multiplication table

For reasons of symmetry we fill in for * = * =
 

0	-	+	+	0	-	-	+	0
0	-	+	+	0	-	-	+	0		0
	+	0	0	-	+	+	0	-		-
		-	-	+	0	0	-	+		+
			-	-	+	0	0	-		+
				-	-	+	0	0		+
					-	-	+	0		+
						-	-	+		+
							-	-		+
								-		+

 
This is the gluon multiplication table in timesymmetric representation. Of course there is a normal representation too. The lower colors shown in the scheme above are changed in their anticolors.
 

The 36 gluons

						white gluons (glue1balls)
						shift +1/6 (vacuum particle)
						baryonic shifts +2/6
						mesonic shifts +3/6
						baryonic shifts -2/6
						shift -1/6 (vacuum particle)