Deriving SR from QM

In the standing still frame, links that link local environments (such as cells in table, or dominoes) to neighboring local environments of the same moment, are changed to different links, when being in the moving frame. In fact that's all there is to SR, changing links between the domino's of spacetime.

In the x-t diagram (the spacetime diagram), when accelerating, the angle of the space axis, the row of now moments, tilts. Imagine driving a car along a straight road (the space axis) and imagine the time axis upward directed, from you to the zenith. When accelerating, the tilting of the space axis then is like the engine bonnet of the front of your car coming up, blinding sight.

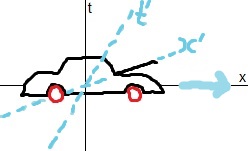fig. 1

There is a clue to the angle of the tilt. The tilt is such that the speed of light remains a constant, c = 3 * 10^8 m/s. The Lorentz transformations are derived using this clue.

But it appears to me that it still needs a force to tilt the angle. Changing velocity, changing frame of reference, needs a force, according to the laws of Newton. That force turns out not only to change velocity, it also tilts the axes of space and time, as it is observed from the outside, the unaccelerated frame of reference.

And I wonder what force that is. Is it a particle, the photon, arriving at the local environment and locally making a choice out of a heap of superpositions? That choice, is that the kind of vacuum particles that surround you? The choice of Higgs field out of the field of all possible velocities? The idea is the Higgs field from which mass is absorbed stands still with respect to the absorbing particle. So far so good, but still unexplained remains why the x- and t-axes would tilt then. They do such that c remains 3 * 10^8 m/s. But why? Just an extra difference to make frames that only differ a velocity distinguishable?

Velocity might be non-existent. Velocity, displacement, might be left out from the theory. Leaving only rotations to the point. It would make quaternions more usable.

Or is the solution somewhere else? The Fourier transformation can transform the wavefunction of a photon of low energy and high uncertainty of place into a photon of high energy and low uncertainty of place. It is this process that shapes or molds the uncertainty relation of Heisenberg.

A low energy photon can be transformed into a high energy photon by you speeding up towards to it. The only thing changing is you, your speed relative to the photon. The photon itself remains untouched and unaffected. The Lorentz transformation then transforms the low energy photon into the high energy photon.

Somehow the Fourier transformation and the Lorentz transformation are the same. The relativistic Doppler equation somehow can be rewritten as a Fourier transform frequency formula.

But it's not me going to do that. Mathematics has never been my strongest point.

Why the fundamental formulas of physics are always so beautifull while their Lorentz transforms are so ugly? (Dirac)

The truth of this remark still is visible for everyone who looks at it. Somewhere in mathematics there must be a road on which the Lorentz transforms are just as beautiful as their original formulas. Quaternions? Quaternions are as to speak specialized in rotation, and the tilt towards each other of the axis in the direction of motion and the axis in the direction of time, IS a rotation.

 

SR and time reversal

Let's regard time reversal in SR.

At page 1 of FORWARD BACKWARD TIME DIRECTION is stated, amongst others:

          :=           and           :=       fig.2

where := means The course of events before the := becomes the course of events after the := by means of time reversal. By time reversal we mean: the film of the events being played backwards.

Let's see whether := not only reverses course of events in time but also yields the proper accompanying SR effects then.

The black bar is e.g. a rocket speeding by, t' and x' are rocket coordinates, x and t are laboratory coordinates (our coordinates). The colored bars are rocket spaces of one specific rocket time, one color bar is e.g. one specific second in the rocket frame.

  fig.2

This is the Minkowski diagram of a rocket with velocity  

 
Fig. 2 := fig. 3

  fig.3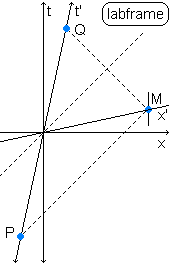  

The := transforms fig.2 into fig. 3, which is precisely the same as fig. 2, except for that the the film of the events is played backwards now (lab frame time arrow t is reversed). Since we read the figure from top to bottom, we see the rocket displacing now from the right to the left.
We conclude the rocket's velocity now is  

The t' rocket time axis has remained the same, it only points the opposite direction now. We repeat a figure from page 2, the last figure at the bottom of the column at the right, that we use to derive the structure of the Minkowski diagram. We see that the light ray now goes from point Q to point M at the mirror that is attached to the rocket's interior, and from M to point P. In doing so it defines the same x' rocket axis.

 
Fig. 3 can be denoted as:

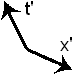    fig.4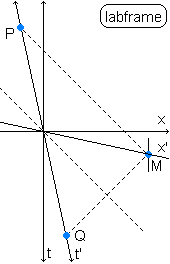

This change-of-denotion encompasses that all horizontal lines fig. 3 consists of and that are drawn one under the other from top to bottom, now are drawn one above the other from bottom to top. It is the mirror reflection with respect to (any line parallel to) the x-axis. It mirrors everything, including the directions of time, so there is no physical change at all, only another way of denoting the same course of events.

As you can see, the rocket's velocity still is

Also the Q-M-P figure is mirror reflected. The light ray still goes from Q via M to P. The x' axis now is tilted (with respect to the x axis) by the opposite angle, perfectly fitting in with the reversed velocity.

So when the film of events is played backward, the accompanying SR effects suit neatly with the reversed course of events.

 

CTL considerations

Only by our memories we are aware of the time dimension, of the elapse of time. The only difference between an ordinary line in space and a timeline on the same place, is the elapse of one moment in time into the next moment in time. It is impossible to stop this transition, to make it not to take place. This transition only happens in one direction.

We only remember one single past. So towards the past there was only one time axis, one time dimension. Towards the future one may assume there will be the corresponding future time axis only. But maybe we would not distinguish between memories build up along one timeline (time dimension) and memories build up along another timeline.

The transition from one moment to the next obeys all kinds of laws. These laws are supposed to be much simpler for a zero dimensional space (a point) and one time axis, forming a line, a timeline, than for a three dimensional world with one time axis.

Suppose the line is a closed string. We stated the line is a timeline and its world has zero dimensions, inhabited by one single quark. The quark is forced from one point on the line to the next.

Suppose a fmo (fast moving observer) in a rocket speeding by looks down to a vast laboratory compound on the Earth's surface. In this storyline is shown that the fmo sees every moment of the laboratory frame simultaneously transform in the next moment of the laboratory frame. However the fmo only sees one plane of the laboratory frame (perpendicular to the direction of rocket motion) per single laboratory moment.

Accept this as a feature of time, how time looks, and apply this look onto our closed string. We are in the lab and the closed string is standing still before us. There is not enough space in the zero dimensional world to exhibit velocities, and so there are no SR effects, but the feature of time is the same, that is what we assume. Then the quark is not somewhere on the string. The quark is simultaneously (in the lab's frame of reference) at every point of the string and every point of the string simultaneously transforms to the next point of the string.

Every moment of our time we see that every moment on the string is passing to the spatial next point on the string, in the time direction, as an action-that-is, as a sparkle of life, that mysterious inevitable transition from one moment the next. It is not that a sparkle displaces from a moment to the next and then to the following next and so on; it is rather that the same sparkle that makes a specific moment to pass onto the next moment happens again and again at every of the observer's moments. Each point of the string has the sparkle al the time (the observer's time). Regarded like that there is not so much difference between a string made of spatial points, without such sparkles, and a string made of timeline points, each of them provided with the sparkle. *)

At a certain moment (a certain of our moments) the string can break, leaving a line segment with two open ends. It tranformed from a CTL to an OTS, an Open Time Segment. The string is not every moment (our moments) the same timeline string. So every of our moments it is a new timeline string that we see. The string in fact exists only one single of our moments. But if the string can be influenced from the outside (that's why we are introducing it) then the entire CTL evolves in the course of time, our time.

Maybe a CTL can break up in two line segments, a quark and an antiquark line segment. However, when the antiquark line segment is turned upside down, it is a quark segment. One has to find something new, a new property that doesn't change when turning upside down. Spiralling is such a property. Take two identical right-threaded screws and put them in line with each other with the blunt sides together. Now hold the two blunt ends between thumb and forefinger in such a way that the blunt parts are both obscured. Now you see one single right-threaded screw with two sharp points at both ends and no blunt part to use for the screwdriver. Turn it upside down and back again. There is no difference.

When every transistion along the entire string doesn't violate any law of nature then the closed string is not contradict, and thus is possible, existable. E.g. for 1 quark in a zero dimensional space there is no way for any entropy development, any entropy increase. So no matter where we start at the string, when we return at our point of departure the entropy will still be the same.

A spatial string filled with three quarks, a baryon, has a red quark, a green quark and a blue one. A CTL with one quark that is three quarks long, exists of three times the same quark, with same color, isn't it? The only action our quark can perform is to emit one or more gluons at the same spot (there is only one spot). The gluons could react with each other. Finally all the gluons can be reabsorbed again, returning to our sole quark in its zero dimensional space.

*) With life we do not only mean life consisting of cells and directed by DNA. We mean the transition from moment to moment, or at least from coupling to coupling, occuring at every particle of the standard model.

Let's start over again. The line is a CTL, a zero dimensional space occupied by one quark in ground state that moves in time along a small circle-like time dimension. The CTL occupies a line in our space, in principle we can see the CTL. We would see then a circle of quarks, each quark provided with the sparkle of time. We see each quark simultaneously transferring from one moment to the next.

The CTL is a tiny universe on itself and doesn't need anything from the outside. In our universe it can and should exist only one of our moments. However, the CTL consists of matter (one quark) that is part of our universe too. So we can assume the CTL has a development in our time too. We see all the time (our time) all quarks simultaneously going from one moment on the CTL to the next moment on the CTL - until there is something that disrupts this. Do we see the CTL only one moment, or does the CTL has a time evolvement in our 4-dim spacetime too?

In this website space is quantized, its quanta (vacuum particles) about 10^-21 m apart. Time is taken to be quantized too, to quanta of 10^-23 sec, the reaction time of the colored strong force. Since the time direction of the CTL is also a space dimension in our world, does one quantum of time on the CTL (10^-23 sec) equal one quantum of our space (10^-21 m)?

Does the quark move along its timeline? Does it displace? The quarks are connected to each other by time transition from one quark to the next, like beads on a string. But the quark doesn't disappear on its spot and reappear on the next. It still is where is was, forever (our forever) passing to the next quark, the quark of the next CTL moment. So the answer seem to be no, the quark doesn't displace along its time axis and no, the quark doesn't have a velocity along its time axis. There only is the reaction time which for the strong force on a quark is set equal to 10^23 per second.

Suppose in our laboratory on Earth a CTL is standing still. Suppose it only existed one single moment of our time and in that specific moment we have an overview of the CTL as described above. A fmo (fast moving observer, although speed smaller than c) speeding by only sees one plane of every moment of us, the laboratory, neatly stacked next to each other in the direction of motion of the fmo and each plane perpendicular to the velocity of the fmo. The laboratory space of the specific laboratory moment that the CTL exists, is split up in planes at subsequent fmo moments.

 

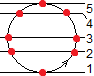
The circle is the CTL, the red dots are the quark on the CTL. The arrow on the circle indicates quark time direction, the direction of time within the CTL. Fmo velocity is in the y-direction. The numbers at the right are subsequent fmo moments.

The fmo only sees one quark in the first and last plane and two quarks in every moment in between. That is, the fmo sees the lowest quark in the figure at a certain fmo moment named 1. At moment 2 the fmo sees two quarks, the left quark transferring to the next quark downwards, the right quark transferring to the next quark upwards. There is no way for the fmo to distinguish upward/downward time transference of the two quarks. At moment 3 the fmo sees the two quarks at maximum distance, the full width of the CTL. At fmo moment 5 the two quarks had merged again to one quark, and the next fmo moment (not shown) the CTL would have disappeared from direct fmo view. (The moment the CTL exists is still there, but the corresponding sheets all lay outside the CTL's location.)

The disappearence of the two quarks at a certain fmo moment, and the simultaneous reappearing of the two quarks a fmo moment later, suggests a velocity of the quarks. At page 5 of this storyline is shown that the speed of one moment of time is greater than c.

Now we crush the circle-like shape of the CTL to a line segment aligned along the direction of motion of the fmo (topological deformation of shape). Our quark now moves in time in the same direction as the fmo does in space. The quark moves onto the end of the line segment, then abruptly changes time direction and then retraces its path in opposite direction, and so on. When the quark changes time direction it becomes an antiquark. When the color of the quark is red, then the color of the antiquark is antired, cyan that is.

The formula shows that when the speed v of the fmo increases, the speed called v(color) of a specific laboratory moment (choose the moment the CTL is visible) slows down as observed by the fmo, until both, fmo as well as the specific laboratory moment, move at lightspeed. That is what page 5 of this storylines points out.

The picture we have now of the CTL at every of the fmo's moments, is a quark antiquark pair, making up a gluon that indeed is assumed to move at c. (For quark pairs making up gluons, see Four quarks in the shell at page 5 of QCD) The gluon moves from one end of the (crushed) CTL to the other end. The space where the quark antiquark pair is, still is a point. So there is no space for the quark and the antiquark to move apart. They cannot form a 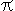meson or W-particle (depending on the color of the quark or antiquark, see the = pairs in the 3rd and 4th scheme at page 5 of QCD).

The minus sign in the formula indicates that the velocities of the frames and the moments-of-time have opposing direction. When the gluon as just described moves at c then the moments of time on the gluon move at c in opposite direction, leading to a kind of standstill of the gluon's moments of time as observed by the outside observer. Likewise for photons and neutrinophotons (for neutrinophotons, see paragraph Neutrinophotons at page 4 of QG.) This helps to imagine how a Bose condensate of gluons or photons or neutrinophotons can form a standing still solid grid as the vacuum is supposed to be in this website.

Surely you're joking, mr. Feynman

At page 24 of a Dutch copy of this book I found the following. Start with a rocket from the Earth and be back when the clock on the ground has ticked away 1 hour. Choose your path such that in the rocket elapses as much time as possible. The larger the height, the weaker the Earth gravitational field, the faster runs the internal rocket clock (GR). The larger the rocket's velocity the slower its clocks run (SR).

It turns out that free fall (no acceleration except from the gravitational field) gives the maximum total elapse of time in the rocket. So you shouldn't use the rocket's engine to navigate. At the start just give a single upward thrust such it is back after a fall of one hour.

Is it an intrinsic property of the theories of relativity GR and SR? What is the advantage for nature of having maximum elapse of time in the rocket frame, does it save energy or something? Is it the quantum mechanical result of the interference of all possible paths that are back in one hour? If the gravitational field wasn't inversely squared but had a different mathematical dependence, would then free fall tracks still ensure maximum elapse of time in the rocket frame? That were the questions that raised when first reading this problem.

Now I red another copy of that book, an English copy, and at page 37 it says: It's the fundamental principle of Einstein's gravity - that is, what's called the proper time is at a maximum for the actual curve, the real motion of matter.

In the first copy of the book it was presented as a riddle to which nobody knows the answer yet. In the second copy Feynman points out it isn't. What I understand now is the following. An object called A in free fall follows a straight line at constant velocity in curved space. In tracing that line it has no acceleration whatsoever due to gravity. (No acceleration means velocity remaining constant, that's the definition of no acceleration.) Any deviation from the straight line that subsequently returns to a point on that line where the rocket is, would cause SR dilation of the clocks in the deviating rocket. Also when the deviator would stick to the track and only accelerates or decelerates, it would cause SR dilation of the clocks in the deviating rocket. It is the same way as the twin paradox arises, with object A as the aged brother at home and the rocket as the traveler brother that stayed younger.

Let's start over again. Rocket 1 in free fall follows a straight line in curved space. A second rocket, rocket 2, starts at that line, side by side with rocket 1, then deviates from it and then returns to a point on the line where rocket 1 is. Now at the point of collission (be carefull, if the rocket 1 orbit is in the x-y-plane, then perform the rocket 2 track one rocket diameter aside in the z-direction) change to a MCRF* that stands still with respect to rocket 1 at the point of collision. To do so you have to perform a Lorentz transform. Then you have the precise circumstances of the twin paradox.

By the way, the answer to the last question, about if the gravitational field wasn't inversely proportional to squared distance, but had a different mathematical dependence, obviously is: yes, the free fall track still ensures maximum elapse of time in the rocket frame.

*) MCRF: Momentary Comoving Rest Frame, or MCFR Momentary Comoving Frame of Reference