Page 4 and 6 of this storyline sum up all arguments that are important when thinking about quarks and gluons in nucleons in this website. Used is the model of a particle absorbing Higgs field to gain mass, and an antiparticle within its time border emitting to the Higgs field. The time border is defined in (21), (22) and (23) in paragraph The calculation of the time border at page 2 of THE EXPANSION OF THE UNIVERSE.

This view is based on the storylines NEG page 3, 4 and 5 and FB TIME DIRECTION page 3. You can skip these pages and read them later as long as you take (7.1) for granted as well as the remarks made above about Higgs absorption and emission.

A little knowledge about quaternions would be nice. Especially several remarks all over the place about the structure of the vacuum, are based on the view introduced at page 2 of QG, Quaternion Gravitation, where this structure is introduced. Keep special attention to the quaternion parts and (try to) skip the colorshift remarks. Colorshift is a concept that is abandoned now. The quaternion approach of strong force colors is worked out in the storyline QQD.

Quark exchange

Can a quark go anywhere? In case of the antibaryon, 3 quarks in an antibaryon, that is in 3 quite nearby points A, B and C can go to 3 other quite nearby points D, E and F along all possible paths this can happen - but always the 3 quarks must remain in close proximity, within 10^-15 meters. In groundstate this necessarily forms a kind of bundle through spacetime made of innumerable paths superposing. For a proton this can be any length, and any length of time, since the proton is stable. So yes, a quark can go anywhere, as long as its companions do agree to follow (nearly) the same path.

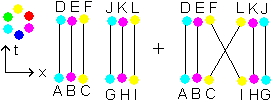
Consider 2 neighboring antibaryons in a nucleus of several antiprotons and antineutrons. Suppose the 2 yellow quarks happened to be identical except for their location (same energy and impulse, both anti-u-quarks and spin +1/2, by example). Then there is a superposition of the yellow quark going from C to F and the yellow quark going from I to L with the yellow quarks going from C to L and from I to F. The start-states and end-states are the same so both possibilities superpose. Although the latter with a smaller contribution due to distance-reduction, since path C-L is a little longer than C-F and I-F is a little longer than I-L.

Mind the 2 antibaryons are supposed to overlap a little. Regard the table in paragraph The proton. Regard the choices we made for A, B and C. When the 2 yellow quarks are neighboring in the overlap area, they are too near to each other and the force between them is too weak. They will recede until force is strong enough. The quarks have aligned spin and indeed will attract each other. Then I imagine they will spin around each other a number of times and when finally let each other go, they are that dizzy that neither of them will have the slightest idea whether they are in their own antibaryon or in the neighbor, and so these possibilities superpose.

The two antiquarks under consideration are of same color only 1/3 of the time, due to gluon exchange in the antibaryon. They have same spin half of the time. Compared to strong reaction time, they do not change taste. Let's guess their impulse-energy range is identical in half the time. Finally, when circling around each other and happen to end up in their own antibaryon, there is no exchange. In only half of the cases there actually is an interchange. So only in 1/3 * 1/2 * 1/2 * 1/2 = 1/24 of the time our two antiquarks do really interchange.

All possible disturbances count with equal importance

When the straight line segment connecting start state point to end state point is included, color disturbances are closed paths in spacetime. Obviously that straight line segment cannot exceed about 1 fm in space and 1 cycle in time.

For every gluon that appears, the coupling constant of the color interaction appears as a factor in the wavefunction. For every gluon that appears and disappears again the coupling constant appears twice. The coupling-constant of the color-interaction is about one and therefore the repetitive occurrence of the color constant as a factor hardly diminishes the amplitude of the wavefunction.

Suppose, a particle sets out from a certain point in an unknown direction. Nothing disturbs the particle, its impulse remains a constant. The amplitude of its wavefunction is reciprocal to the traveled distance because the surface of the sphere of all points where the particle can be after a certain time, increases with the square of the distance. We accept this to hold for quarks and gluons too. But the gluons emitted by a baryon (3-quark system) often return to that baryon to conserve white end state there. Nowhere color may be left exposed. If colors travel closed paths and when the colors approach their origin again, the wavefunction's amplitude will increase and finally precisely cancel out the initial decreasing.

So all possible disturbances count with equal importance; almost equal. There are 2 exceptions to this rule: glueballs and neighboring baryons.

Glueballs

In this site each of the superposed reactions is taking place in its own world, having a reality experience of its own and taking the time and space it needs for completion. It experiences itself as the only disturbance taking place at that moment on that place. It doesn't see the other possibilities, the other disturbances. Despite its status as superposed virtual reaction, every disturbance happens in a complete world that obeys all known laws of nature, like the conservation law of energy, impulse, etc.

A glueball just leaves the baryon and the amplitude of its wavefunction is reciprocal to the traveled distance. They cost a lot of energy to form, we assume, so their abundance, rate of occurrence, is low. The glueball's high energy gives a lot of possible, existable particle assemblages with identical overall properties guaranteed by the conservation laws. E.g. the possibility the gluon splits in 3 gluons (step 1). Three gluons merge easier than two, see page 7 of this storyline. Each of the three gluons decays in a quark-antiquark pair (step 2), that rejoin crosswise (step 3) and then the gluons rejoin again to the single gluon (step 4). It all are massless universes, in a sense that there is no net Higgs field absorption and thus no gravitation and no time. The superposed gluon universes take no time - that is, not from our time.

Every moment the world splits in as many worlds as there are possibilities for the glueball assemblage to evolve to, to be something. That can be just the same glueball or one of the other possibilities. Assemblages that are unstable decay as soon as possible, in doing so preventing an eventual turning back to the original glueball assemblage. This holds as an observation and you find yourself back in one of them, not seeing the other possibilities no more. The universes then do not rejoin to one universe. In every universe there is another you, eventually evolving differently from now on. This is the decay model of this site in the mind of page 2 of EXPERIMENTS ON THE COLLAPSE OF THE WAVEFUNCTION.

Neighboring baryons

Can photons observe the baryon and terminate a chain of color reactions? The idea is: the photon observes a quark (it is absorbed or emitted by a quark in the nucleon) and then the nucleon to which the quark belongs must have settled its color condition at white, despite the fact that the photon only sees the quark's electric charge and not its color.

In the nucleon there are two kinds of electric charge: the u-quark with +2/3 and the d-quark with -1/3 unit of electric charge. In the proton p = uud there are (2 + 2 + 1) / 3 = 5/3 charges present, in the neutron n = udd, there are only (2 + 1 + 1) / 3 = 4/3. The neutron offers 1/3 charge less than the proton to couple with the photon, that is 20 % cross section less for photons to hit the neutron. So per second the neutron is hit 20 % less than the proton, there is 20 % more time between two subsequent incoming photons. If color reach is restricted by photon observation, the color reach of the neutron is expected to be 20 % larger than the reach of the proton.

(Maybe neutronium - matter made from 2 or more neutrons - exists inside the nucleus. There is no net electromagnetic force working on the neutronium to propel it outside or just outside the nucleus. There are only color forces keeping it within.)

The minimal typical electromagnetic reaction time is about 10^-20 seconds. A single source (particle) cannot create photons at a higher pace. So one can have an observation of a baryon by a photon (e.g. from another baryon), then 10^-20 seconds spare time and then the next photon comes in. In 10^-20 seconds a lightspeed gluon covers 3 x 10^8 m/s * 10^-20 s = 3 x 10^-12 meter. This is back and forth since the gluon path is closed. So when restricted by photon observations the reach of the gluon would be about 10^-12 meter: 1000 times farther than the actual reach of the gluon is.

In one proton plus one neutron are present (2/3 + 2/3 + 1/3) + (2/3 + 1/3 + 1/3) = 5/3 + 4/3 = 9/3 = 3 units of electric charge. So to restrict color range by photon observation one needs 10^-12 / (3 x 10^-15) = about 400 or 300 times more nucleons to create the photons needed than there are present.

It obviously doesn't work like this.

The Light Speed - Planck Constant - conjecture

Finally I want to end with a few conjectures. The habits in renormalization theory are described by Feynman as immoral. However, the backward evolving of time has been justified using the view of this site, e.g. experiment 2 (page 2 of EXPERIMENTS ON THE COLLAPSE OF THE WAVEFUNCTION about that superpositions are universes on their own) and the theories of gravitation (page 3 of NEWTON EINSTEIN GRAVITATION) and backward time gravitation (page 1 of EXPANSION OF THE UNIVERSE). At paragraph What is a coupling? at page 4 of THE DIRECTION OF TIME is offered a way how the curved paths of photons in some Feynman diagrams can come to be. This leaves the FTL-behavior (Faster Than Light) of the virtual particles as immoral, as well as that at a lot of routes the photons seem to move slower than c.

What is the difference between the universes in the superposition and our universe? I guess its mass, its local gravitational field strength, its local number of Higgs field absorptions per cubic meter. Low mass universes, like those superposed in QED and QCD renormalization, have in fact infinite upper velocity - that's how we calculate with them! Does this mean these universes have infinite lightspeed? (Lightspeed then is more an upper velocity as defined in SR and not specifically the speed of photons.) If so, then lightspeed may be higher for lighter universes, approaching infinite lightspeed in a zero mass universe. All relativistic effects would vanish in low mass universes.

But dependence of lightspeed from local gravitational field strength means light would speed up when further away from the sun and this is not observed in e.g. delay times in the covering of Jupiter's moons by Jupiter.

Maybe low mass universe should be universes of low number of particles in it. How does a particle know how much other particles the universe contains? Renormalization theory as in QED implies that a particle is every moment visited by at least one virtual particle from every other particle in the 4-dim universe, no matter how far away those other particles are or how far in the future or past. Is this a measure for the number of particles in the universe?

I used to think that the Paradox of Olbers, that holds for brightness of starlight, also should hold for gravitational strength since they both obey inverse square dependence of distance. A mass should undergo a same amount of gravitation from every shell of same thickness around it, no matter how far away that shell is or how many shells there are. If there are infinite shells then on any object on Earth there is an infinitely strong gravitational pull from all sides. But the paradox of Olbers is solved, see page 7 of THE EXPANSION OF THE UNIVERSE. Those infinite influences are not there, not for light and so not for gravitation too, is the opinion now.

Another conjecture is (46) in paragraph Quark mass at page 4 of QCD.

Yet another conjecture. Keep the Sommerfield fine structure constant α at constant, in doing so keeping the atom sizes at constant. Allow c to approach infinity while h approaches zero in such a way that the product hc remains at constant.

α = (1 / 4 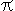ε ) ( e / 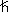c ) = e / (2 hc ε)

Also the energy of the photon, E = hc / wavelength, doesn't change then.

I wonder how QED and QCD renormalization would behave when this is performed. When c approaches to infinity and h approaches to zero one gets a Newtonian universe. How a Newtonian renormalization would be? It reminds me to Mr Tompkins in Wonderland. In this book h becomes larger and c becomes smaller. Did George Gamow considered this kind of arguments, then gave up and finally made a wonderful story about it?