Acting on a photon without destroying it

This was an awful lot of philosophy again. Let's try to investigate how it actually works for a particle.

Is it possible to perform an act on a photon without destroying it? When a beam of light impinges on a surface of glass 4 % is mirror-reflected and 96 % is refracted according to the law of Snellius. But when analysed in QED there are no photons that are reflected or refracted. In QED there are only 3 actions possible:

    1) An electric charge goes from one position to another;

    2) A photon goes from one position to another;

    3) An electric charge emits or absorbs a photon.

It is said that all of optics and electromagnetics and all of QED can be derived from these 3 actions alone.

A photon can only be acted on by an electric charge. Photons only couple to electric charge but if they do the photon is absorbed. These 3 actions offer no possibilities for a photon to be acted on without being absorbed by an electric charge. So no, it is not possible to perform an act on a photon without destroying it. Or is it?

A photon goes from location 1 to location 3. Somewhere on its route, on a place called 2, happens to reside an electron. The photon can go from 1 to 3, just passing through the electron as if it wasn't there (upper light ray in fig.4). It also can be absorbed by the electron at 2, immediately re-emitted again and go from 2 to 3 (lower possibility). When we cannot distinguish these possibilities then they are in superposition.

For this superposition to be apparent, the photons 1-to-2 and 2-to-3 (Abbreviate to ph 1-2 and ph 2-3) need to be of the same energy and spin, travelling in the same direction along the same line, with perfectly suiting phase and no loss of time at the coupling - just as if the coupling had not taken place. At the part of the path before 2 the photons ph 1-2 and ph 1-3 are identical and merge to one photon-state. The photon hadn't decided yet to couple to the electron or not; the world hadn't yet split. At the part of the path after 2 the photons ph 1-3 and ph 2-3 are identical and merge to one photon-state again.

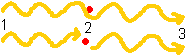          fig.4

The resulting wavefunction of the photon is a superposition of ph1-3 and ph 1-2 + ph 2-3:

P(13) + P(12) * j * j * P(23).

The wavefunctions (ph 1-3) and (ph 1-2 + ph 2-3) are not equal. In the latter the coupling constant of the electromagnetic force j (which is nearly 1/10) has occurred twice as a factor, one time for absorption (when the photon is destructed) and once again at emission (when a new photon is created). This reduces the contribution of this possibility by a factor of nearly 100. So the wavefunction of a photon is affected by an absorption-and-reemission, even if the reemitted photon perfectly suits to its predecessor: its amplitude is reduced.

So the unaffected ph 1-3 contributes about 99 percent to the endstate of the photon. The absorbed and reemitted ph 1-2 + ph 2-3 contribute about 1 percent. If there is no time-loss at the coupling then the coupling ph 1-2 + ph 2-3 as described above, is always strengthened by a just-passing-by ph 1-3. The ph 1-3 nearly replaces the ph 1-2 + ph 2-3, the endstate ph 1-3 + ph 1-2 + ph 2-3 is only slightly different from the photon's wavefunction when there had been no electron there.

Have we acted on the photon? For about 1 percent yes, we have. Is the photon absorbed? For 99 percent no, the photon is not absorbed.

When entered, this state will generally turn out to be a just-passing-by ph 1-3. The photon is not destroyed but we didn't act on it either. When entered, in some cases there will turn to have been acted on the photon (by the coupling) but the photon is destroyed and then revived again. When we want to have a photon in QED that is acted on without being destroyed we mustn't enter a state. We are bound not to observe the photon. This means the reasoning so far holds for virtual photons only. Photons from which we shall never know for sure if they did or didn't couple to the electron. And then only when the coupling takes no time and causes no time-loss when occurring.

But even when the coupling takes no time then still our goal - to change to a different past of the photon - remained to be not achieved. No matter if the photon is or isn't acted on, the photon has precisely the same past.

What is a coupling?

The coupling might be a process taking time, with details in it, things to happen in the time-interval. The things that happen can remain pointlike all the time or they can occupy some space of some dimension. Electrons and photons may have shapes evolving during the coupling.

At page 7 of my storyline NEWTON EINSTEIN GRAVITATION I present an approach to the coupling in which the coupling takes no time nor space at all. But well, this approach is not yet worked out properly and is not in use.

At page 4 of my storyline QCD, paragraph Gluon average speed, I found some arguments about the strong force coupling time.

In superstrings a coupling takes time and the strings take space. But does the coupling-process cause a delay in the photon's path? If the process happens at lower than lightspeed velocity there would be a time delay. If at light speed, the timedilation is infinite, leaving no time at all for the process to evolve. At this stage it looks if the coupling in superstrings does cause a delay in time. Unless…

Space has 3 dimensions and the 4th is time. At a point we have an electron. Through the electron's location go lines in all possible dimensions. Take the line in the direction of the 5th dimension and curl it up in the direction of the 6th dimension. Curl the line in the direction of the 7th dimension up in the direction of the 8th dimension. Curl the 9th dimension up in the direction of the 10th dimension. You have created now a 3-dim snipeworld (see margin at the right), a torus with a 3-dim surface in a 6-dim space. The torus and our 3-dim space share precisely one point, the location of the electron - and that's not because of the curvature of any dimension nor is it because of the curling-up of dimensions. The torus is flat (zero curvature) and so is the 6-dim embedding space. The coupling can take its space and time in the torus. An extra time dimension is needed to serve the process in the torus, isn't it? The incoming and outgoing photon go “through the same door at the same moment but in opposite directions” (I hope that isn't a problem). As observed from our local environment the coupling then does take no time.

The torus-space is just a possibility joining the point of our electron. Therefore its overall properties are the same as our local environment. Its 3-dimensionality, the laws of physics holding there, the elapse of time. Does creating an empty universe like this cost energy? If so then the least energy is taken by the maximum curled-up empty torus (providing the minimal non-zero-but-finite 3-dim content) with no curvature and occupying only 1 point of our 3-dim space. The lesser the energy of the torus, the more abundant its occurrence.

Another possibility, superposed with the one in the previous paragraph:

Take the line of motion of the photon at the electron's location. Superpose with it a line that at the electron's location has precisely the same direction but before and after the electron is curved in the direction of the 5th dimension. The line and our 3-dim space share precisely one point then, the location of the electron. The line leaves our 3-dim universe there, in this case because of the curling up of the line. It loops its small curled dimension before it arrives back at the electron's location again. There they “go through the same door in same direction at the same moment of our time”. The line can curl up or down in the direction of the 5th dimension, both possibilities are superposed. [Figure] At the location of the electron lines in the direction of the other 2 dimensions of our space are curled up in the same way, respectively in the direction of the 6th and 7th dimension, each in upward and downward curled version. They form a torus again of a 3-dim zero curvature surface in a zero curvature 6-dim space. A rushing-in photon at the electron's location then splits in 3 photons, 1 going the upward curled route, 1 going downward and 1 going just right through without reacting with the electron. There is no extra time-dimension needed, as far as I see.

Should we consider such far-fetched possibilities? We know the coupling exists. QM subsequently learns that along with the coupling will superpose all other possibilities according to which the coupling also could have taken place. The only demand is existablility. So yes, provided they can exist, we should incorporate such possibilities.

Page 3 up to and including page 6 of NEG says the vacuum is a flat, uncurved structure of vacuum marbles. There is curvature caused by Higgs absorption, but each start of curvature is immediately reflattened by the act of gravity. So essentially spacetime is flat. Both examples of spacedistortions treated above are flat spaces only. So that fits in so far. TONE also says there is no space behind the space, there isn't a higher dimensional space made of vacuum marbles in which our 4dim spacetimes are embedded in. That means that the actual way e.g. the mentioned tori are bend, is not defined. Each loose way of folding would suffice, there is no way to distinguish them. We don't have to consider all these way of folding. Flatness of the bend spaces is the only demand. So it seems yes, the proposed models contribute.

When I was younger I used to imagine particles as 3-dimensional blobs changing shape as a preparation for merging or splitting, a bit like the liquid model for atomic nuclei. For quite a time I used to image the blobs as made of a something that coheres. QED supposes the electron (and the photon too) to consist of a horde of virtual photons and virtual electron-positron pairs. The electron, and the photon too, resembles a galaxy made up of stars rather than a single pointlike particle. But all these constituting particles are in superposition with respect to each other. They don't see each other. The cloud of virtual particles doesn't cohere. (The possibility of all particles reacting does contribute, but is diminished in amplitude by a factor of about 10 to the power of the number of involved particles because of the repeated occurrence of the electromagnetic coupling constant. So this possibility plays no role.)

The case the coupling delay time is zero, should be better considered as the limit of the coupling delay-time approaching to zero. Or are there possibilities? In one possibility the coupling takes time, in the other it doesn't, and depending on situation they superpose?

When the coupling does take time, in the example just described the mimicking reemitted photon (the ph 2-3) may trace the path of the unaffected photon (the ph 1-3), but it stays behind a little. It stays behind twice the time it takes to couple (let's call it the couplingtime), and twice the distance a ray of light can cover in that time (the couplingdistance). From the moment the photon reaches the electron, the wavefunctions (ph 1-3) and (ph 1-2 + ph 2-3) are distinguishable now. When measured we will enter just one of them. We enter 1-to-3 and the photon is unaffected. We enter the ph 1-2 + ph 2-3 state and the photon is destroyed and replaced by a new one.

In the previous paragraph we declared that when the coupling takes no time, the photon has precisely the same past no matter the photon is or isn't acted on. Our goal, to change to a different past of the photon, hasn't been achieved.

Can the photon emitted at 2 come from a different direction?