The volume of the sphere

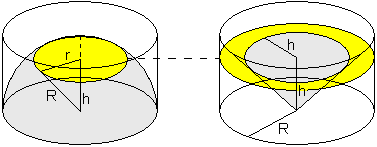
R = radius of the sphere

r = radius of the yellow circle (left picture)

(left picture)

Pythagoras: R = h + r so r = R - h

Surface of yellow circle = r = (R - h)

(right picture)

Surface of the yellow ring around the cone

= surface of the outer circle - surface of the inner circle

= R - h

= (R - h)

At every height h the surface of the yellow ring around the cone equals the surface of the yellow circle in the hemisphere.

Therefore the volume of the hemisphere equals the volume within the cylinder outside the cone.

Volume hemisphere

= volume cylinder - volume cone

= r * r - r * r / 3

= 2 r^3 / 3

Archimedes (287 - 212 b.c.)
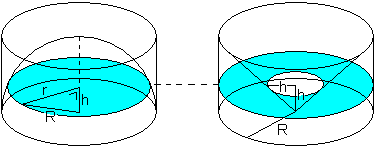
Archimedes found the ratio (the volume of a cone with circular base and height of half the base diameter) : (the volume of a half sphere of same base) : (cylinder of same base and height) = 1 : 2 : 3.

He had it inscribed on his gravestone. He actually found that a horizontal plane intersection with a half sphere and with the volume IN the cylinder but OUTSIDE the cone have same surface at same height. From this he concluded the bodies must have same volume.

The surface of the sphere

Dapple the surface of a sphere more or less regularly with dots.

Connect the points such that there emerges a more or less regular distribution of more or less regular n-sided polygons.

There has emerged a more or less regular polyhedron.

Connect the vertices of the n-sided polygons with the center of the sphere.

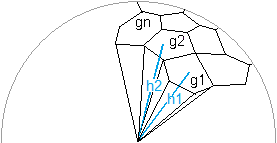
The volume of the more or less regular polyhedron

= sum of the pyramids with the n-sided polygons as base

= g1 * h1 / 3 + g2 * h2 / 3 + ... + gn * hn / 3

As n approaches infinity, the volume of the more or less regular polyhedron approaches the volume of the sphere, the surface of the polyhedron approaches the surface of the same sphere and all heights hn approach the radius r of the sphere.

Let approach all heights hn to radius r first. (Officially this is not allowed. All mentioned properties approach infinity simultaneous.)

The volume of the more or less regular polyhedron

= g1 * r / 3 + g2 * r / 3 + ... + gn * r / 3

= (g1 + g2 + ... + gn) * r / 3

= Surface of the more or less regular polyhedron * r / 3

Volume of the sphere = Surface of the sphere * r / 3

Volume of the sphere = 4 r^3 / 3

Surface of the sphere * r / 3 = 4 r^3 / 3

The surface of the sphere of radius r = 4 r

This is precisely 4 times the surface of the circle with radius r !

There is one more theorem (without proof) found in some textbook. The shaded band on the surface of the sphere is the horizontal projection of the black band on the enveloping cilincer.

The shaded band and the black band have equal surface

The vertical surface of the cilinder is the sum of joined black bands. The surface of the sphere is the sum of the joined corresponding shaded bands. So the surface of the sphere equals the vertical surface of the enveloping cilinder.

The surface of the sphere of radius r = (2 r) * (2 r) = 4 r

2r * 2r can also be interpreted as circumference * diameter of the sphere. This looks a little bit as what we started with: in a circle holds that circumference / diameter =