The surface of the circle

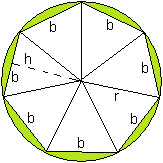
A regular n-sided polygon (the white part inside the green circumference) can be divided in n congruent isosceles triangles (two sides equal) with their top in the center of the n-sided polygon and their base on the circumference of the n-sided polygon.

Surface of n-sided polygon

= hb/2 + hb/2 + ... + hb/2   (n terms)

= n * hb/2

= nb * h/2

= (circumference of the n-sided polygon) * h/2

For n approaching infinity the surface of the n-sided polygon approaches the surface of a circle, height h approaches to the radius r of the circle and the circumference of the n-sided polygon approaches to the circumference of the circle of radius r.

The surface of the circle

= (circumference of the circle) * r/2

= 2 r * r/2

= r

The surface of a circle with radius r = r