Three tetrahedrons in a prism

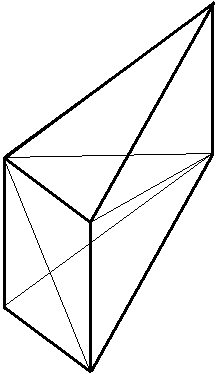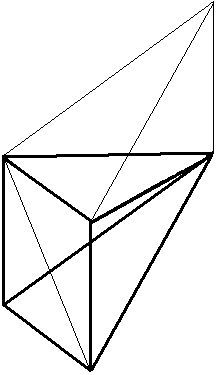
(1)       (2)

A tetrahedron is a pyramid with a triangular base area and three sides.

The triangular prism (a prism with a triangle as base area) can be divided in three tetrahedrons (1).

The triangular prism can also be regarded as a pyramid (made of two of the tetrahedrons) with a rectangle as base and four sides. The third tetrahedron is placed on one side of it (2).

       

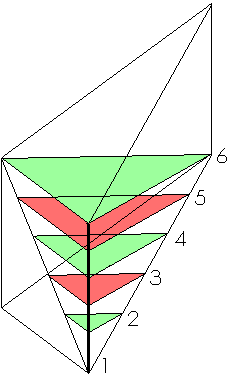
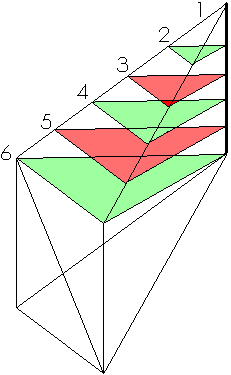
We now compare two tetrahedrons and do that three times. first we pile up green and red triangles in two different tetrahedrons. All triangles are parallel. Identical triangles have same number and same color. As you can see, the two compared tetrahedrons consist of precisely the same triangles, stacked along two parallel line segments of same length (the thick black lines). So the two tetrahedrons have same volume.

   

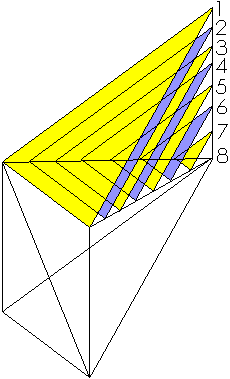
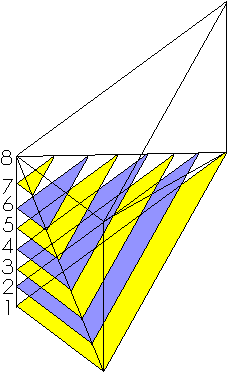
A tetrahedron can be approached by a stack of n triangles of thickness h/n, h is the length of the line segment perpendicular to the base area, along which the triangles are stacked. When you shift the triangles along their surfaces, the total volume of the stack doesn't change. By shifting triangles in the stack one transforms the tetrahedron in subsequently the two other tetrahedrons. When n approaches infinity, the stack approaches the tetrahedron.

   

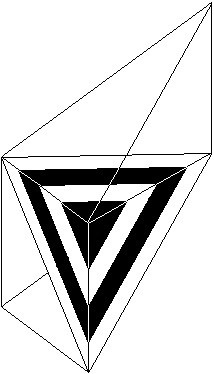
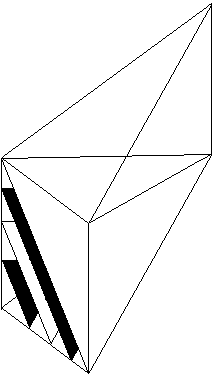
It is clear: the 3 tetrahedrons have same volume.

volume of the tetrahedron

= volume of the prism / 3

= base area * height / 3

             

Eudoxos of Knidos (circa 400 - 340 b.c.)
Eudoxos found the ratio between the volume of the pyramid and the volume of a prism of same base area is 1 : 3.