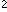The theorem of Pythagoras
Next two figures are congruent.

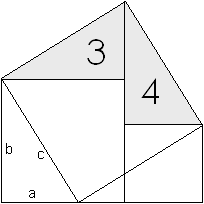
The right-angled triangles 1, 2, 3 and 4 are congruent.
The surface of the entire figure
= 1 + 2 + the big white square (left picture)
= 3 + 4 + the middle-sized white square + the small white square (right picture)
Surfaces of triangles 1 + 2 = surfaces of triangles 3 + 4
The surface of the big white square
= surface of the middle-sized white square + surface of the small white square
Surface of the big square = c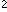
Surface of the middle-sized square = b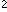
Surface of surface of the small square = a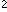
c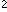 = a
= a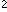 + b
+ b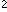
Theorem of Pythagoras
Circa 531 b.c. Pythagoras himself most probably found a precursor of the theorem that is named after him. Probably his school later found the actual theorem.
Limits can be deceptive
Consider the length of the stairs. Regard the left stairs at side a. The stairs consists of the horizontal line segments 1 up to and including 6 plus the vertical line segments a up to and including f. Now displace all horizontal line segments downward to b1. They now form line segment b1. Then displace all vertical line segments to the right to h. They form line segment h.


The length of the left stairs
= length of all horizontal line segments + length of all vertical line segments
= b1 + h
As n approaches infinity, the upper red line and lower green line approach each other and become one single line, the oblique side a of the triangle. The stairs gets an infinite number of infinite small steps and cannot be distinguished from oblique side a anymore.
The length of the oblique side = a
So is a = h + b1? And likewise c = h + b2?
To get a better picture as n approaches infinity, follow this on two screens simultaneously: a static one where you see the steps of the stairs becoming smaller and smaller and finally disappear between the two approaching lines. And a second screen that zooms in with n. There, as to speak, it is the outside world that expands to infinity, while the objects in the second screen (the steps of the stairs) don't change shape or size. In the second screen you always see the stairs can be distinguished from the oblique side a, no matter how large n grows.
However, this holds for most if not every of the used approximations so far. We used the approximation method in The surface of the right-angled triangle
, The surface of the circle
, The volume of the prism
and The volume of the pyramid and the cone
. There is was right. In the case of the stairs it is not. And to be frank, I don't directly see why, or why not.
The length of the left stairs = h + b1. The length of the right stairs = h + b2.
The length of oblique lines a and c are given in
a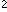 = h
= h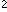 + b1
+ b1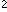 and c
and c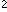 = h
= h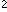 + b2
+ b2