The volume of the prism

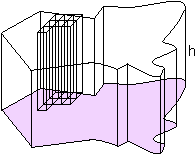
Take a base area of one piece and arbitrary shape (purple area). Displace a copy of the base perpendicular to the base area up over height h. Connect all corresponding points of the circumference by vertical line segments of length h. All these line segments together form the side surface. This figure is called a prism (of arbitrary shape).

Approach the prism by n bars of vertical height h and horizontal square surface g of 1/n of the total (estimated) base area. The picture shows 7 bars.

One bar is a rectangular block of volume gh. The volume of the prism is approximately the sum of the volume of the bars.

Volume prism =

= gh + gh + ... + gh   (n terms)

= (g + g + ... +g) h

= (estimated base area) * height

For n approaching infinity, the estimated base area approaches the base area and the volume of the estimated prism approaches the volume of the prism.

Volume of the prism = base area x height

The volume of the cylinder

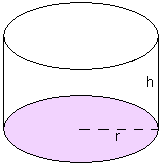
A cylinder is a prism with a circle as base area.

The volume of the cilinder with radius r = base area x height = r h