Volume of the pyramid and the cone

You can regard the tetrahedron as a 3-sided pyramid with the 4th side as its base.

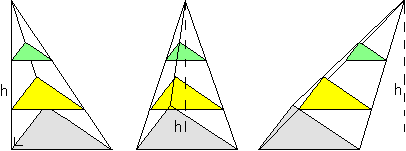
All 3-sided pyramids of same base area (grey triangles) and same height h consist of precisely the same triangles stacked upon each other along the same height, and therefore all those pyramids have same volume.

Every pyramid with a n-sided polygon as base area (n > 3), can be divided into n 3-sided pyramids with base area g1, g2, ..., gn.

           

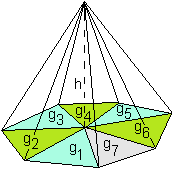
Volume pyramid

= g1 * h / 3 + g2 * h / 3 + g3 * h / 3 + ... + gn * h / 3

= (g1 + g2 + g3 ... + gn) * h / 3

= surface n-sided polygon * h / 3

Volume of the pyramid = base area x height / 3

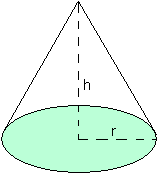
When the base area of the pyramid is a regular n-sided polygon and n approaches infinity, the base area approaches a circle and the pyramid approaches a cone.

Volume of the cone = r h / 3