Symmetry




On can regard the Minkowski diagram as a table consisting of cells neatly ordered in rows and columns. In fig. 3 below one can distinguish the horizontal rows and vertical columns of the x-t laboratory frame. One can also distinguish the tilted rows and columns of the x'-t' rocket frame.

An event marks a point in spacetime, approximated by the cell it is in. Two events that coincide will keep coinciding no matter in what frame observed. Two events in the same cell that are divided by a small space or time very well may reside in different cells when observed in a different frame.

One cell represents a point in spacetime. In fact it is not a point but a one-moment slice of space perpendicular to the rocket's velocity. You have by example the slice the laboratory L is in. The appropriate column then is the history of that slice.

The laboratory experiences one moment of its x-y-z-t system of rods and clocks at the time. They call it the now and now they experience the whole system of rods and clocks passing to the next moment. In fig. 3 one horizontal row is clearly one moment of laboratory space, one moment of the Earth's system of rods and clocks.

In the laboratory they were just testing a new way of spacetime status transferring. They first replace each laboratory frame cell of the Minkowski diagram by 3 numbers, one above the other. The Minkowski diagram was converted into a table. These 3 numbers are:

  rocket time t' (determines the color of the rocket in that cell);
  laboratory time t (Earth time);
  laboratory x-coordinate (the position of the cell in the laboratory-frame).

Rocket frame position x', the fourth number, is not shown.

The 3 numbers in a particular cell are undividedly attached to each other as the numbers of one domino stone, no matter in what frame observed. One very well may consider the surface of a cell of spacetime to be the domino stone's surface. For the moment the dominoes maintain relative position precisely like the cells they replace in the Minkowski diagram of laboratory spacetime. The surface of the table is the structure of spacetime.

Unfortunately the laboratory M turned out to fall just in between two domino's.

The part of the Minkowski diagram they transformed to a number-scheme concerns a length of 7 rocket colors on 5 subsequent moments in the lab-frame.



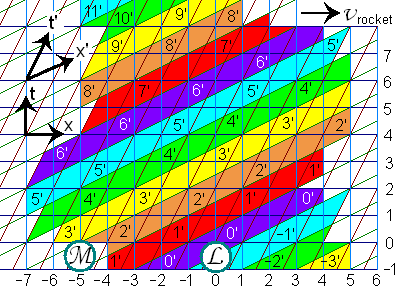
Minkowski diagram


Fig.3 The Minkowski diagram in the laboratory frame can be considered to consist of cells.



9'
6
-6		 8'
6
-4		 7'
6
- 2		 6'
6
0L		 5'
6
2		 4'
6
4		 3'
6
6
 
8'
5
-6		 7'
5
-4		 6'
5
- 2		 5'
5
0L		 4'
5
2		 3'
5
4		 2'
5
6
 
7'
4
-6		 6'
4
-4		 5'
4
- 2		 4'
4
0L		 3'
4
2		 2'
4
4		 1'
4
6
 
6'
3
-6		 5'
3
-4		 4'
3
- 2		 3'
3
0L		 2'
3
2		 1'
3
4		 0'
3
6
 
5'
2
-6		 4'
2
-4		 3'
2
- 2		 2'
2
0L		 1'
2
2		 0'
2
4		 -1'
2
6

arrow to the right   Rocket velocity

Regard the first block, 9' 6 -6 . The 9' is measured along the first tilted yellow bar. The 6 and -6 are to be taken along the horizontal and vertical axes respectively. 9' 6 -6 is one single point with coordinates 9', 6, -6. The x' coordinates are not shown. In this way 7 x 5 = 35 points are written out here.


In the rocket they have a similar time experience. The rocket passengers also experience one rocket-moment of their system of rods and clocks at the time and then that rocket moment passes to the next rocket moment. In the cockpit the captain had just asked the operator if the laboratory had already sent their new spacetime status.

Yes captain! the operator said. He had just got transmitted the domino scheme as showed above and gave it to the captain who gave it a close watch. The captain lifted his eyebrows.

What kind of nonsense is this, Karl? he cried out. All the times were lying in a heap!

This is what they told us, sir, the operator said. This is how they see us, they say.

But we don't see us like that, don't we? asked the captain.

No sir the operator replied.

Be so kind, detach those slices and put them in the right order, please! the captain said. The operator got at work. After a while he finished the job and gave the reordered scheme to the captain. This is what he got:



        9'
6
-6		     
      8'
6
-4		  8'
5
-6		    
     7'
6
- 2		  7'
5
-4		  7'
4
-6		   
    6'
6
0L		  6'
5
- 2		  6'
4
-4		  6'
3
-6		 
   5'
6
2		  5'
5
0L		  5'
4
- 2		  5'
3
-4		  5'
2
-6
  4'
6
4		  4'
5
2		  4'
4
0L		  4'
3
- 2		  4'
2
-4		  
3'
6
6		  3'
5
4		  3'
4
2		  3'
3
0L		  3'
2
- 2		  
  2'
5
6		  2'
4
4		  2'
3
2		  2'
2
0L		    
   1'
4
6		  1'
3
4		  1'
2
2		     
    0'
3
6		  0'
2
4		      
     -1'
2
6		       
arrow to the left   Earth velocity


Yes, that's right! the captain replied. That's how we see us! The scheme is a little fragmentary but the pattern is clear. Do you see it is them who consist of slices of all different times?

And Karl did see it. He had been the first to perform a Lorentz transformation on laboratory spacetime coordinates.

The table Karl constructed consists of the same domino stones as the laboratory table. You can reorder domino stones in a spacetime table but you can't separate the numbers of one domino stone. The last table showed rows of equal rocket time. The rocket is standing still now, it's the Earth that is moving in opposite direction. The velocity of the Earth is represented by the inclination of the line of L's in the table. For the table to meet rocket Minkowski spacetime (lightrays always at 45 degrees angle) the inclination rate of the line of L's should be equal to the inclination rate of the t' rocket time axis in the laboratory Minkowski diagram (fig.3).

The empty cells in the table are no gaps. It only meant the scheme had been represented better when spacetime measurements were given by a factor 2 more accurate. Then the gaps would have been filled with the intermediate measurements. The leaning line of equal laboratory times betrays the dissynchronization of the laboratory times in the rocket frame. The inclination of the line of equal laboratory times should be equal to that of a rocket band of one color in the laboratory Minkowski diagram (by example a yellow band).

Two frames that are moving relative to each other see each other dissynchronized.

They also see all each others lengths contracted along the direction of motion. They see each others clocks running slower - also timedilation is symmetric between frames in motion relative to each other.

When relative velocity slows down to zero then original sizes are restored. The other frame regains its normal lengths, clocks are no longer dissynchronized and all run at the same pace again. That is, time itself is running everywhere at the same pace again. All phenomenons characteristic for SR disappear except for one.

In the frame that has undergone acceleration the amount of timedilation build up so far, becomes real. Acceleration realizes timedilation.

Gravity is not distinguishable from acceleration and therefore also gravity realizes timedilation. But that is GR, general relativity.