High above the earth, its nearest point just behind the orbit of the moon, a rocket passes by. It's a very huge ship, its diameter is about that of the moon, it length at least a lighthour. From the earth one can see the large round windows at its side. Its speed approaches that of light and so, despite the rocket seems to span the whole sky, the show will be over within an hour.

In the ship the light is changing all the time. One moment (moment 1' rocket time) a passenger on board sees the whole rocket illuminated in red, one second later (moment 2' rocket time) the whole rocket is orange. On moment 3' the rocket is all yellow and on moment 4' the rocket is in green. Then follows blue and violet and then the cycle starts over again with red, orange, yellow, etc. - six seconds for one color cycle.

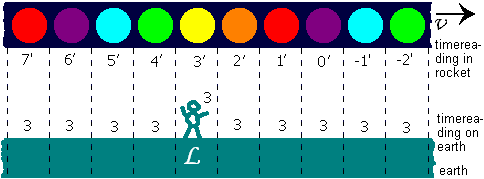    fig.2

If we say a rocket passenger sees the whole rocket in red (let's assume the interior being a whole, no partitions whatsoever) then we of course mean afterward collected observations as agreed upon in the previous page.

What does a rocket passenger actually see in direct vision? Suppose the passenger has a seat somewhere in the middle of the rocket. The diameter of the moon is often listed as 3474, 3475 or 3476 km. Let's fix the diameter of a rocket window on 3000 km, a little bit smaller than the moon. The speed of light is about 300,000 km/sec. With a window diameter of 3000 km, a passenger will still see approximately 100 windows around him or her in the same color (by example red). Light that arrives from further away than one lightsecond has the color of one second ago (violet). Light from further away than 2 lightseconds has the color of 2 seconds ago (blue). And so on. In direct vision a rocket passenger sees, counted from his or her place to areas further away in both directions, the order red-violet-blue-green-yellow-orange-red-etc in subsequent rocket compartments. Since the next color is up to 300,000 km away, a telescope is advised. But we don't use direct vision. We collect observations afterwards.

Suppose you are standing on the earth, on a place called L at a moment called 3 (see fig.2). What does the earthly bound observer see then of the rocket colors? You can see the color of a compartment through the round windows. According to Newton is 1=1', 2=2', 3=3' and so on. But according to Einstein this is only the case when the rocket is motionless with respect to the earth. The rocket moves by with nearly lightspeed. Now we see something quite different.

We see the rocket in a rainbow of window colors, see fig.2. Here we meet the first of two most important phenomena in sr: timedissynchronisation. Around you it is moment 3 all over earth. But at that same moment on earth you see the rocket as divided in slices of different rocket time. The slices are perpendicular to the direction of motion. Slices to the right show rocket time of the past (the past of the rocket) and further past in proportion you go further right. Slices to the left show rocket time of the future (the future of the rocket), and further future in proportion you go further left. Only the slice right above you, the slice you're in now, lists earth time, the same time as you are in on earth. The 3 and the 3' should be placed right above each other. At moment 3 earth time you're in the 3'-moment rocket time.

This is afterward-collected time-measurements only. What does one see in direct vision? For reasons to become clear in the next pages a description has to wait.

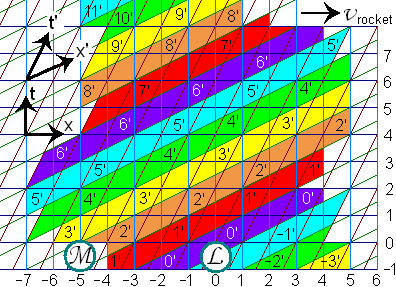
Fig.3: The Minkowski diagram
Figures at the right and lower side are the t and x laboratory coordinates.
The t' rocket coordinates are drawn in the picture, the x' rocket coordinates are not mentioned.

Let's pick out earth-moment 3.

Fig 4: Moment 3 on earth. If at that earth-moment one makes in mind a step to the right or to the left you arrive in a different rocket-moment

But mind, making a real step takes time. One cannot do that in one single earth-moment. The maximum speed for such a step is the 45 degrees lightspeed angle. In this type of diagram that is not a very high speed and it lead you out of moment 3 to the next moment all too soon.