Shall we experiment a little?

Start with the well-known time dilation formula from SR

t' = t / SQRT( 1 - v / c )             (12.01)

t = time in frame 0, t' = time in frame 1, t'' = time in frame 2, and so on. All frames differ a velocity. Frame 0 sees frame 1 to have velocity v, frame 1 sees frame 0 to have velocity -v. Displacement s = vt, s' = -vt'. 1ijk-space = quaternion space, xyzt-spacetime = our well-known spacetime. Take in mind two events A and B and set the Origin in A.

t' = t / SQRT( 1 - v / c )

( 1 - v / c ) t' = t

t' - v t' / c = t' - s' / c = t

(c t') - s' = (c t) - 0 = ...

The 0 means s = 0, we just set s at zero.

SR states the interval (c t) - s is a constant for all frames:

(c t) - s = (c t') - s' = (c t'') - s'' = (c t''') - s''' = ... = constant             (12.02)

When you take the Lorentz transformations t' = ... and s' = ... and fill them in in (c t') - s' then you find (c t) - s.

In fact this is all there is to SR. It is called the invariance of the interval. When there was no SR then in an x-t-diagram would have hold the theorem of Pythagoras, (c t') + s' = constant for all frames. The t-axis and the axes x, y and z would be perpendicular to each other in all frames. Lengths along the t axis would have been treated just like lengths along x, y or z. So only this minus sign is the difference between Newton spacetime and Minkowski spacetime. Can quaternions provide this minus sign?

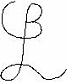
Take time t to be real and take displacement s' to be the length of quaternion q = fi + gj + hk. A rectangle with sides a meter and b meter has surface ab m. A length of b meter squared is b m. Likewise squaring length fi yields (fi) = f i = -f. Quaternion unit i is regarded as measurement unit like the meter, and so are j and k. Then

s' = f i + g j + h k

= -f -g -h             (12.03)

(c t') - s' = (c t)

(c t') + f + g + h = (c t)             (12.04)

Which is the ordinary Pythagoras theorem in 1ijk space.

If you take time as real and take space dimensions as imaginary and take SR for granted, then 1ijk quaternion space reacts as xyzt spacetime, as far as spacetime coordinates and the distances between them are concerned.

I sometimes call this the real-imaginary swap. It has to be admitted that other properties like surface and volume are not directly recognized as working the same in 1ijk and xyzt space.

1ijk is a richer space. In 1ijk space length a times width b is height c, where if a * b = c then b * a = -c. When changing from 1ijk to xyzt spacetime, the height dimension property is lost, leaving only a real number there. The two possibilities ab = c and ba = -c are reduced to ab = ba = c. Compare the transition from wavefunction to probability division by by taking the length (the modulus) and squaring it.

Something like this minus-sign one also meets in (3.02) at page 3 of QQD:

(-1 + i + j + k) (-1 + i + j + k) = -2 -2i -2j -2k = -2 ( -1 + i + j + k)

Try it yourself in the excel document baryoncollision.xls

A previous attempt

                        

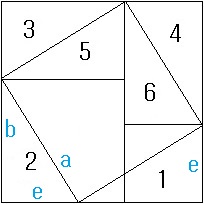
Triangles 1 up to 6 are congruent.
1 means the surface of triangle 1, and so on.

a + 1 + 2 + 3 + 4 - b

= e + 3 + 4 + 5 + 6

a - b = e

a + (b * i) = e

Generalize this to

a + (b * i) + (c * j) + (d * k) = e

a - b - c - d = e

This resembles the invariance of the interval,

t - x - y - z = a