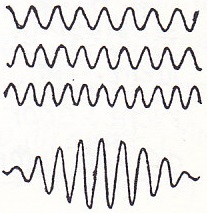
Infinite long waves, equal everywhere and forever the same

Quotes from

FTL? (Faster Than Light)

by Chiao, Kwiat and Steinberg,
Scientific American August 1993, page 43.

Infinite long waves, equal everywhere and forever the same. A wave plus another wave with a little larger frequency and a wave with a little smaller frequency gives a pulse-like object. Adding sufficient frequencies yield a real pulse or wave-packet. A larger spread of added frequencies yield a shorter pulse. A smaller spread gives a longer pulse.

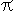Δf * Δt 1/4, this holds for every kind of waves.

E = hf -> ΔE * Δt h/4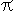, uncertainty relation.

f = frequency, Δt = pulse duration, h = Planck's constant.

Usually the blue pulse speed is a little slower than the red pulse speed, causing dispersion: an originally white pulse changes into a rainbow-like longer pulse, the reds a little ahead, the blues a little behind.

Every kind of glass has dispersion, also bundle splitters and mirrors suffer this. When a photon passes through glass of 2.5 cm thick, its pulse width is 4 times as large.

One such wave, infinite long, equal everywhere and forever the same, is equal to a photon of infinite precise frequency and thus infinite uncertain place and time (uncertainty relation). It is a photon and so it has an existence on its own, just like the usual photons.

Call this a field frequency, one frequency out of the field of all possible frequencies.

Imagine a real particle, e.g. an electron, to exist in one definite state. Observation of a particle always goes by means of another particle, there is just no other way. Take our electron to be observed by a photon.

Take the photon as a superposition of an infinite number of nearly equal field frequencies taken out of the field of all possible frequencies. The phase of each frequency is taken identical at one specific location. That location then is the maximum of the pulse's amplitude and is the location of the photon.

Subsequently the electron absorbs the photon. The electron is observed simultaneously by a herd of nearly equal photons, resulting in a similar herd of observed electron states. The electron then exists in a superposition of a quite narrow group of nearly identical state guided by the uncertainty relations of Heisenberg; just as the original photon already was.

When the electron then emits a photon, it is this herd of electrons in superposition that all at the same moment and at the same place emit one specific frequency out of the field of all possible frequencies, one such infinite long wave, equal everywhere and forever the same. The phase of all emitted photons is identical at the moment of emission. The electrons in superposition were nearly identical and after the emission they are identical. The electron's definite end state is the result of all possible ways the electron could have arrived there.

The electron is in one definite state back again. The photon is a herd of nearly identical frequencies again.

One starts with a single state electron and a herd of photons in superposition. Then the photon is absorbed and is gone, and the electron splits in as many electrons as there were photon states. The herd of electron states each emit a photon. The electron states merge again to the single state as it had at the start. Simultaneously the herd-of-photons superposition is restored. Usually this process is described by the uncertainty relations of Heisenberg. In the process there is no collapse of a wavefunction.

This paragraph describes the coupling between a photon and an electric charge. Paragraph There is one more peculiarity to view at page 2 of the storyline EXPERIMENTS ON THE COLLAPSE OF THE WAVEFUNCTION, tries to take into account spin.

Gluons and photons outside of time

There are only two massless particles in the Standard Model: the photon and the gluon. They have net absorption zero from the Higgs field and thus no mass and no gravitational field. Aren't they entirely “outside of time” as well? (See the conjecture at page 6 of QCD) Their entire world line? It seems to fit in with the following two points.

1) Because of SR time is standing still at the photon. It will be so at the gluon as well. So we will not miss events happening at the photon. Such events are not there. For the gluon we would miss all gluon-gluon couplings.

2) According to QED the photon does not exist as a localized particle. You cannot clip a part of empty space, e.g. a cube meter, with a photon in it and say Look, I caught a photon!. According to QED the photon travels all possible routes from source to goal and when you clip a part of space with the photon in it, only the most important contributions are in there. But not all the other contributions that visit all points of spacetime outside the clipped part. It would be convenient if all those reactions would have a place outside of time, where they can do their job without being hindered by usual limitations like causality and the speed of light. (Feynman said Particles are immoral there!) Is this candidate for ground below the QED picture?

One is tempted to suggest renormalization from QED would work as well when only the photons travel all paths from source to goal and that the electrons don't. But the two slit experiment works with electrons instead of photons as well. So no, that cannot be, isn't it?

O  NVESTIGATE

The field of all possible frequencies

The article of T. H. Boyer, The classical vacuum, Scientific American august 1985, discusses the zero-point radiation field.

The article makes clear a Lorentz invariant field of all possible frequencies has to be of intensity I f^3    (f = frequency).