Application 4: Baryons

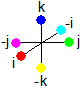
IF kji = 1 is color neutral THEN -k * -j * i = 1 is color neutral too (i, j, k, -i, -j, -k are quark colors, 1 and -1 are gluons).

This is in fact an application from the Minus Sign Go Wild approach at page 3 of QG. Not true for observed end states. Maybe true for unobserved intermediate states, the so-called virtual particles? The immoral virtual particles (as Feynman called them) in renormalization procedure go backward in time, faster than light and its photons move in small curves wherever required. So maybe more immoral behavior can be expected between the virtual particles under consideration.

	1		2		3		4		5		6		7

 
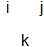
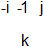
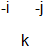
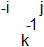
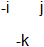
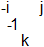
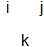
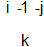
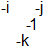
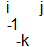
This would violate the conservation of color, but such a law is not yet known. The only law used is the everything-overwhelming urge for color neutrality. And that a color cannot just like that on its own change in another color; to do so is needed a color particle like is used here -1.

The transition from b1 (baryon 1) to b3 is caused by -1 going from i to j (b2) OR by -1 going from j to i (b2 below). The emitting color is divided by -1 and the absorbing color is multiplied by -1. The two possibilities b2 and b2-below cannot be distinguished and superpose. Compare the usual color swap between colors by means of a colored gluon.

The transition from b3 to b5 is caused by -1 going from -j to k (b4 up) OR by -1 going from k to -j (b4 below). Also these two possibilities superpose.

But wait, in b4 below, couldn't the -1 escape? -1 itself is colorless and it leaves behind a white antibaryon. Normally, in ground state: no, energy not available. But when energy is sufficient to provide the free -1's mass, then yes. IF this can be, then we have a baryon with antibaryon colors.

We consider now the single -1 gluon emission only. Starting from b1, an ordinary baryon, there are 6 different ways to arrive at a b3-like state (i > j meaning -1 gluon going from i to j)

i > j, j > i, j > k, k > j, k > i, i > k

and 3 ways to remain in the b1 state:

i > i, j > j, k > k.

All -1 emissions have same chance, and so have all -1 absorptions.

( When an i emits a -1, the -1 is initially nearest to that i, eventually giving it the first chance to absorb. So there might be a little enhanced chance for i > i, j > j and so on. We take this effect negligible. )

At b3 there are 7 ways to stay in a similar state (with 1 plus-color and 2 minus-colors, 1 color and 2 anticolors that is)

-i > k, k > -i, -j > k, k > -j, -i > -i, -j > -j, k > k

and 2 ways to return to the original baryon state:

-i > -j, -j > -i.

The total number of steps is 6 + 3 +7 + 2 = 18, yielding a net number of steps of 6 - 2 = 4 towards the one color and two anticolor state. So when starting with a population of b1-likes one soon ends up with a population of b3-likes, with only a few b1-likes. The ratio of plus-color abundance to minus-color abundance then is 1 : 2 or 1/3 : 2/3. Is there a connection with the -1/3 and +2/3 electric charge of the d- and u-quarks in a baryon?

According to the representation of the vacuum in QUATERNION GRAVITATION page 2, even when the reactions shown above would not take place, then a baryon state b1 will absorb one (-1 -1) vacuum marble to arrive at state b3. Subsequently it will remain in that state as argued.

Mark that IF we would still work with gluons with an upper and a lower color, instead of a quaternion unit replacing the gluon, that THEN in -k * -j * i = 1 some of the 12 so-called unused gluons would be used there.
 

   and   

 
E. g. and would swap i and -j. See the gluon table.

 

Still application 4: Mesons

	1		2		3		4		5
	i       -i		i   -1   i		-i       i		i   -1   i		i       -i
	i        i		i   -1  -i		-i      -i		i  -1   -i		i        i

 
The lower mesons are no mesons, it are colored end state objects, despite their colorless outcome -1 in multipliction, i * i = -i * -i = -1. See the text below (3.41) in paragraph Mesons at page 3 of QQD (the first 7 alineas).

Mark that if the upper meson nr 1 is u u (thus the left quark is u with color i and the right quark is u with anticolor -i) that then the upper middle meson nr 3 is at the left the same quark u with anticolor -i and at the right the same antiquark u with color i. It are a quark-with-anticolor and an antiquark-with-color, but since the overall color composition is maintained, there seem to be no objection to it.