When I started in 2012 to identify nuclear colors with quaternion units I did that on morphological grounds only. When a few years later I stuck on the existence of Pauli matrices and matrices for quaternions, this identification turned out to be much nearer to the core than expected. The 8 Gell-Mann matrices are the 8 gluons. The first three Gell-Mann matrices contain the 3 Pauli matrices as their core. Multiplying two Pauli matrices yield a quaternion unit which is a gluon in my theory. I experienced it as surprising and encouraging.

Quaternions as 2 x 2 matrices

Quaternions (left side of equation) can be represented as 2 x 2 matrices (right side of equation).

a + bi + cj + dk =           (9.1)       *)

Mark the upper row in the matrix contains already all necessary variables a, b, c and d. The second row is “junk”, extra machinery necessary to keep the matrix running. When you take a, b, c and d and set three of them at zero and set the fourth at 1 or -1, then you get the quaternion unit matrices.       *)

*) Mind the i in the left side of the equation is the quaternion unit i, while the i in the right side of the equation is the complex number i (two-dim plane of one real axis and one imaginary axis).

1 =         i =         j =         k =         (9.2)

-1 =       -i =       -j =       -k =         (9.3)

SU(2) is the following group:

SU(2) =             (9.4)

where the overline denotes complex conjugation.

When you substitute α = a + bi and β = c' + di and c' = -c, then you get eq. (9.1) again. SU(2) then is the 3-dim surface of a 4-dim sphere in a 4-dim space with 2 real and 2 imaginary dimensions. While quaternions cover all of a 4-dim space with 1 real and 3 imaginary dimensions. That is not the same. But the matrices are the same and therefore I dare to state:

Quaternions are SU(2)               (9.5)

S HIS   ORRECT?

SU(2) has 2 real dimensions and 2 imaginary dimensions is satisfied in (any quaternion unit) = (a Pauli matrix) x (a Pauli matrix) when you take axes 1 and i from the first Pauli matrix orthogonal to the axes 1 and i from the second Pauli matrix. This means that the two Pauli matrices are completely independent, isn't it? So IF the Pauli matrices here can be orthogonal THEN quaternion 1ijk space can be SU(2).

In QM orthogonal states exclude each other, isn't it? It is one or the other, but not both. Are the Pauli matrices states here? In quaternions there is some ambiguity. A quaternion can define a rotation (an operator, I guess) as well as a point in 1ijk space (a state). Pauli matrices are a kind of "square roots" from quaternions, a kind of factorization, see in the column aside at the right.

Pauli matrices

There are three Pauli matrices: sigma 1, sigma 2 and sigma 3, denoted as s1, s2 and s3.

s1 =         s2 =         s3 =         (9.6)

When two Pauli matrices are multiplied, one always gets a quaternion unit.

		s1	s2	s3
s1		1	i	-j
s2		-i	1	k
s3		j	-k	1		(9.7)

(9.7) means s1 * s2 = i, s1 * s3 = -j, and so on. Seven quaternion units 1, i, j, k, -i, -j and -k are formed, but -1 isn't. -1 times a Pauli matrix like s1 just yields -s1. It doesn't yield a quaternion unit. So I don't place the matrix of -1 next to s1, s2 and s3.

1 =             -1 =             see (9.2) and (9.3)

		1	-1
1		1	-1
-1		-1	1		(9.8)

This means that everywhere in this website you can replace every quaternion unit by the appropriate Pauli matrix product. After replacement there is no quaternion no more anywhere in this site.           (9.9)

Nevertheless, if you do so the quaternion calculation formalism remains intact as long as you always and everywhere keep the Pauli matrices of one Pauli matrix product together.           (9.10)

A Pauli matrix usually means a particle, e.g. the electron, or a quark in this case. Two Pauli matrices in multiplication usually mean two particles in interaction, e.g. a collision. Two Pauli matrices staying in multiplication then mean two particles in continuous interaction, like in a composite.

According to Four quarks in the shell at page 5 of QCD the gluon is a composite of a quark and an antiquark that approached each other within their time borders. If each quark is given by one Pauli matrix, then the two quarks together are given by two Pauli matrices in multiplication. That then is the gluon. The two quarks making up the gluon are independent from each other and so are the two Pauli matrices of those two quarks.

There is another way of representing quaternions, by real 4 x 4 matrices (real means that there only are used real numbers in the matrix), very useful when one has a matrix multiplication app to ones disposal, see quaternions. Or see References link nr 2 below. This seems to indicate that quaternions are SO(4).

Quaternions are SO(4)               (9.11)

Maybe one best says that quaternions are SU(2) and that they can simulate SO(4). Something like that.

However, each of the two quarks composing a gluon has color too and each color consists of two Pauli matrices. So this is not so simple, especially since the quark and antiquark in the gluon do not merge but stay apart as separate particles.

O   NVESTIGATE

The gluon as quark antiquark composite is worked out in the storyline QCD, especially Meson exchange at page 4 and Four quarks in the shell at page 5.

Remark (9.10) means that the gluon remains intact as long as the constituting quarks remain together, within their time borders. This is obvious since when the quarks are separated you have to provide their mass and that showed to be impossible so far.           (9.12)

The color i of a quark consists of two Pauli matrices s1 * s2.

For quaternions holds ijk = -1. From (9.7) we know

i = s1 * s2,

j = s3 * s1 and

k = s2 * s3. So

ijk = s1 * s2 * s3 * s1 * s2 * s3 = -1

So -1 can be formed from 6 Pauli matrices in multiplication.           (9.13)

-1 turns out to be a glu3on, see Three gluons applied together at page 3 of this storyline. Page 7 of QCD shows that

3 gluons merge easier to 1 gluon than 2 gluons do               (9.14)

Or otherwise, from the 3-gluon composite two of the gluons might be absorbed in the shell of the third gluon, see Four quarks in the shell at page 5 of QCD. A single -1 gluon should remain then.           (9.15)

i = j = k = -1, so

s1 * s2 * s1 * s2 = s3 * s1 * s3 * s1 = s2 * s3 * s2 * s3 = -1

So -1 can be formed from 4 Pauli matrices too, two gluons that are. But as said, 2 gluons merge less easy than 3 do.           (9.16)

Gell-Mann matrices

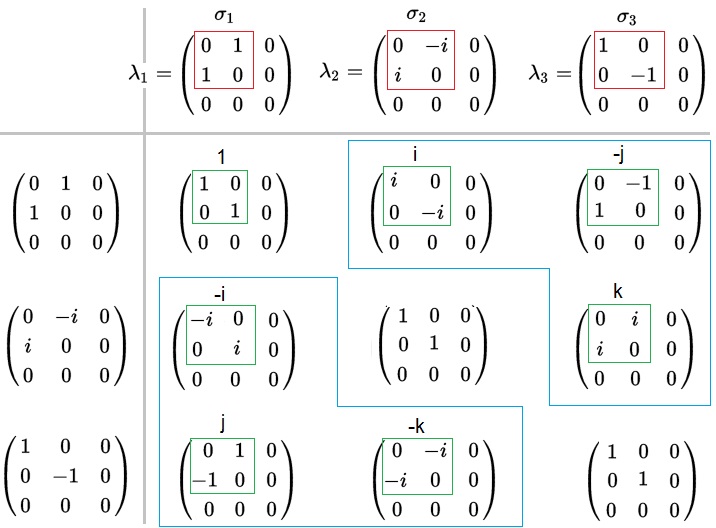
This scheme shows the first 3 (out of 8) Gell-Mann matrices λ1, λ2 and λ3 and their products. These products are in fact the matrices I propose as gluons. The red frames are the Pauli matrices σ1, σ2 and σ3. The green frames are the quaternion units, except for -1. The large blue frames together are one subset. The Gell-Mann matrices λ4 up to and including λ8 (not shown) are not to be used.

According to the view of this storyline in fact all Gell-Mann matrices are not to be used anymore.           (9.20)

Resemblances and differences of QQD versus QCD

What makes me think the quaternions of SU(2) can mimic the Gell-Mann matrices of SU(3)? A summary of resemblances (green numbers) and differences (red numbers) between QCD gluons (part a) and QQD quaternions (part b).

1a) There are 3 colors that together give something that has no color no more.

1b) There are 3 imaginary quaternions that when multiplied with each other, give something that has no imaginarity no more: ijk = -1 en kji = 1.

2a) The 3 colors together give white, a kind of “7th color that isn't a color”.

2b) The 3 imaginary quaternion units, when multiplied with each other, give 1 or -1. When 1 is called white then -1 is black . Black and white, instead of white only.

3a) Red * green = green * red = antiblue, or yellow: * = * = . The order of multiplication is not important.

3b) In quaternions the order of multiplication is important:
i * j = k en j * i = -k.
There is little other way than to accept there are often two possible outcomes, when colors meet. The possible outcomes superpose. They can cancel each other. Or double their value in the wavefunction.

4a) Every color has one anticolor.
and (or red and cyan),
and (or green and magenta),
and (or blue and yellow).

4b) Each of the imaginary quaternions has one opposite:
i and -i,
j and -j,
k and -k.

5a) A color and the appropriate anticolor give something that has no color no more and that is white.

5b) An imaginary quaternion unit times its opposite gives something that isn't imaginary no more and that is 1.
i * -i = 1
j * -j = 1
k * -k = 1

This is the case in our forward time evolving space. In backward time evolving space, as observed by us, it is:
i * -i = -1
j * -j = -1
k * -k = -1
An imaginary quaternion unit times its opposite gives something that isn't imaginary no more and that is -1. See Dark multiplication rules below.

6a) One can order the 6 colors in a 2 dimensional colorcircle. White, an eventual 7th color, can be thought of being placed in the middle of the circle.

6b) The imaginary quaternion units form 6 points in a 3 dimensional coordinate system. The 7th unit 1 and the 8th unit -1 are quaternion units on the real axis. The real axis is a 4th dimension then (not shown). Does this mean SU(3) is replaced by a kind of SU(2) X O(1), with 2 subsets [i, j, k, -i, -j, -k] and [1, -1]?

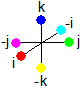
7a) Red can transform to green by a red-to-green gluon.

7b) A color like i can transform to the color j by multiplication with the gluon j/i. Just like in complex numbers dividing by i is the same as multiplying by -i. However, j has to be LEFT-MULTIPLIED by -i:

j/i = -i * j = -k, see page 1 of this storyline, eq. (1.15)

When a quark of color i transforms into a quark of color j by the gluon j/i, the quark color i has to be RIGHT-MULTIPLIED by the gluon -k:

i * j/i = i * -i * j = i * -k ( = j ).

Both in gluon absorption as well as in gluon emission, the color always has to be right-multiplied by the gluon, see Page 2 of this storyline, eq. (2.3).

8a) There are 8 gluons, 6 of them have color, 2 of them are colorless (both white).

8b) There are 8 gluons, 6 of them have color, 2 of them are colorless (white and black respectively).

Will the b parts make things easier and simpler than the parts a? When so, maybe things can be calculated that in SU(3) are very difficult and doubtful, if not impossible.           (9.30)

References

(1) https://en.wikipedia.org/wiki/special_unitary_group for the matrix of SU(2) and the Gell-Mann matrices.

(2) https://en.wikipedia.org/wiki/quaternion for the matrix of the quaternions.

(3) https://en.wikipedia.org/wiki/pauli_matrices for the Pauli matrices.