Counting interactions

My quest for comprising gravity as a netforce started in real matter.

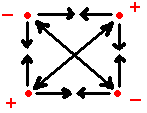
Assemble two positive electric charges and two negative electric charges in a square as shown. At first glance one might say "There are two positive charges plus two negative charges, so the total charge is zero and so the total force is zero too". But when counting the number of attractions and repulsions, one sees there are four attractions and only two repulsions. The repulsions act over a little longer distance than the attractions and thus are weaker. The net force isn't zero at all. Under the electric force alone this square should implode! At least at first moment.

One can see the forces perpendicular to the plane of the charges are zero. And the forces on each charge are equal and symmetrical. So one can expect the square to remain a square while imploding. Which means the contraction will continue.

Lets go one dimension higher, not 4 charges in a square but 8 charges in a cube.

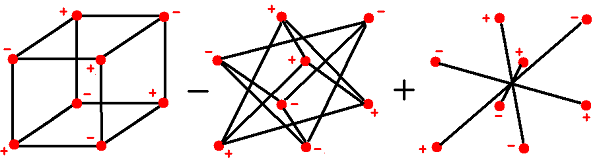
Now we have:

12 attractions of strength 1 in the first figure

minus 12 repulsions of strength 1/2 in the second figure

plus 4 attractions of strength 1/3 in the last figure

= 12 - 6 + 4/3 = 6.75

(The distances of the repulsions in the second cube are SQRT 2 times the distances of attraction in the first cube, according to Pythagoras, SQRT = square root. The strength of the electric force falls with the inverse square of the distance. The distances of the attractions in the third cube are SQRT 3 times the distance of an attraction in the first cube.)

We have effective nearly 7 attractions of strength one more than repulsions. So this cube will contract too. For reasons of symmetry one may expect the cube staying a cube while contracting. At first glance it looks stable too. So also this contraction will go on and on.

Does this hold for more charges?

Suppose we start from a large but finite cloud of an even number of positive and negative charges, homogeneous distributed over space and in a homogeneous distribution of charge. This is the most stable distribution. Every excess of one kind of charges anywhere tends to spread until it is smeared out over the cloud of charges as much as possible.

For simplicity we assume their masses all to be equal and at one certain moment of time t all charges are standing still relative to each other.

Select from the cloud a sphere with n positive and n negative charges in it and neglect all other charges as if they weren't there. ("click them off")

The total number of attractions in the remaining sphere is

# attractions = n

(the number of negative charges times the number of positive charges)

The total number of repulsions is

# repulsions = 2 * 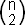= n - n

(all possible pairs in the group of negative charges plus all possible pairs in the group of positive charges)

The net force is the total number of attractive interactions minus the total number of repulsive interactions

netforce = n - (n - n) = n

So in a cloud of n positive and n negative charges there are n attractions more than repulsions.

The electric force falls with increasing distance. It is only for this reason we try to maintain a maximum homogeneity of spatial and charge distribution. Then the distances of the repulsive interactions are assumed to be distributed in the same way and to have the same weight as the distances of the attractive interactions.

As a result a contracting force is working all over the cloud at moment t. The cloud is going to contract, at least at first moment t.

Does the spatial distribution of the 2n charges in the cloud keep its shape while contracting? For symmetrical reasons the contracting force is directed to the sphere's center all over the cloud and one may expect this stays like that. But the strength of the force, isn't it stronger at the center and weaker the more one goes towards the surface? Or is it the other way around? I should my simulation keep running again and then I can see. Let's suppose for the moment the force is the same all over the cloud.

Suppose we go back to moment t and we take an extra (2n+1)th charge and place it in an appropriate way in the frayed edge of the sphere. We do this simply by slowly enlarging the sphere's radius and, if necessary, displace the center of the sphere a little, until precisely one of the "clicked-off" charges is enclosed in the sphere too and "click it on" again. This ads 2n interactions to the cloud, n attractive and n repulsive ones. But if someone who has never seen the cloud before, is coming to look at the cloud after we added our (2n+1)th particle, that person will not be able to judge which particle it was that we had been adding! In the same way the cloud itself will not be able to tell the new particle from the rest.

One could argue that the cloud consists of an even amount of well-mixed positive and negative particles of equal mass and will be electrically neutral with respect to an extra particle outside. But at this moment this person might definitely be pointed to the fact that the cloud is in fact a multipole, an electric field that is the sum of all monopole electric fields of the individual charges. The result may look neutral from large distance but at close detail it should reveal a very complicated pattern of outgoing and ingoing fieldlines that are nearly straight lines originating in the center of the sphere.

So if the particle accidentally happens to lie on an outgoing fieldline it would recede from the cloud. It would be repelled, our questioner insists.

Well, here the homogeneity of the spatial and charge distribution should come to the rescue. It would provide every charge is always a little bit more surrounded by it opposites than by its equals which should make it always lying on an inward directed fieldline - anyway, I think the repelling field line will go into space, turn around there and speed back again into the cloud of charges. The particle will always return. That holds as an attraction!

Well, this sounds a little bit fuzzy, but all right, usually this indeed might be the case. But then still the (2n+1)th particle added n repulsive interactions and n attractive ones, which still are supposed to cancel each other out nearly completely. So no matter what fieldline it is on in the resulting multipole field, this is of no significance. Our extra particle will fall behind while the rest of the cloud starts to contract.

But then, which one was our particle? Which particle will remain behind?

Because the cloud doesn't distinguish between its 2n+1 particles no one will stay behind. There is just no other way.

In other words: a negative (and likewise a positive) charge will be attracted by a neutral cloud of n positive and n negative particles.

The contraction only will proceed a little slower. The estimation calculated above now is:

# attractions = n (n+1) = n + n

# repulsions = 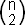+ 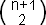= n (n-1) / 2 + n (n+1) / 2 = n

netforce = n + n - n = n

So we still have n attractions more than repulsions. This cloud will contract.

The next step is to remember which one was our (2n+1)th particle and then again slowly enlarge the sphere of charges (and if necessary displace it a little too) so that it encompasses another particle, of opposite charge this time, just next to our (2n+1)th particle. For educative reasons we assume this succeeded this time.

What do we have now? At first we made the cloud electrically neutral again. It now consists of n+1 positive and n+1 negative charges. So according to preceding reasoning this cloud is going to contract. But we might interpret the two new particles (number 2n+1 and number 2n+2) as a new mini-cloud. That cloud contracts because we made the particles being each others opposite. The rest of the cloud, being the n positive and n negative charges with which we started, contracts too. And since the whole cloud of n+1 positive and n+1 negative charge will start to contract anyway, we may interpret this result as follows.

The electrical neutral cloud of n+1 positive and n+1 negative charges and the electrical neutral cloud of our two new particles are attracting each other.

although a little too fast maybe, we draw from this the general conclusion that two neutral clouds of electrical charges with a homogeneous spatial and charge distribution (which is an equilibrium-condition), will attract each other.

Localforce

Non-relativistic and non-quantum mechanical research on electrically neutral multipoles shows in general that the netforce of a number of 2 to the power of m charges on a charge outside is inversely proportional to the distance to the cloud to the power of m+2 :

netforce of charges 1 /

So you see, the well-known inversely square Coulomb-law only appears for m=0, = 1, that is for one single charge only.

So the netforce of a very small cloud (just a few numbers of pairs) on an outside charge may be significant on a small distance (like a few times the distance between the charges of one pair). The netforce per charge is significant then. But the netforce of a little larger cloud falls all too rapidly with the distance to be of any importance on a little larger scale. We can conclude:

The netforce of a charge distribution in a cloud as mentioned above only works local. Let's call this a localforce.

Which means that for a charge in the cloud only the nearest parts are important for the netforce. The rest of the cloud can be neglected. The whole cloud can be considered to be a patchwork of border-overlapping localities, stitched together by the netforce. One patch only attracts adjacent patches and when the localities contract, the patchwork as a whole contracts too. Patches further away have no significant influence no more.

The patchwork acts as elastic matter, in which also tensors are used, just as in GR, General Relativity; although calculation that it exactly acts as in GR, is lacking. It acts too as a jar of glueballs sticking together, reminding to the strong nuclear force that is working over short distances only. Nowadays is used the view of my storyline NEG (Newton Einstein Gravitation), you can start at page 3 The Higgs Field - Part 1.

What precisely is one locality? As mentioned above, this seems to be just one single charge. The electric field of one single charge has the least decrease with distance and hence the largest range, making the patches maximal.

When you begin with on pair of charges - one positive and one negative - and subsequently add more and more of such pairs, the total mass of the charge collection will increase proportional to the number of charges (except for the mass defect, a usually small effect from special relativity). But the increase in netforce remains far below proportionality to the number of charges. For one pair the force falls with r^3, for 2 pairs the force falls with r^4. According to the formula above there is a decrease proportional to the distance to the cloud to the power of the number of charges. At a fixed distance with a huge number of charges the netforce will be diminished by that distance to the power of that huge number of charges.

The formula of the netforce has a peculiar property with respect to that distance. If you position yourself on distance 1, you get 1 to the power or m+2, which is always 1. So at this special distance you may add as much charges as you like, but the diminishing-with-the-distance-effect will not work here. For distances even smaller than 1 one becomes a strong increase of the power with increasing number of charges. This distance 1 must be a special constant. I mean, it cannot be you can choose it arbitrarily. The force then would have no definite behaviour at a certain distance, by example in the case of adding charges, if you always might be able to choose that distance to be 1.

So we have now:

An electrically neutral cloud of charges contracts under the electric force of single charges which work only local. Two of such clouds, when in close contact, will merge.

In REAL MATTER the netforce seems to take the shape of the so called Van der Waals force. The Van der Waals force is inversely proportional to the 6th power of the distance. In the formula above this means that m+2 = 6 and so m = 4. One patch causing netforce has 2^m charges, 2^4 = 16 charges consisting of 2^3 = 8 positive ones and also 2^3 = 8 negative ones.

In QED the vacuum is filled with even amounts of electrons and positrons, as well as even amounts of mesons and antimesons, protons and antiprotons, and so on, however all in different relative densities. Particles swiftly popping in and out of existence too fast for detection, in doing so forming a cloud in which one expects a contracting netforce. The acquired velocities of the individual particles would vanish with them all the time, being replaced as they are by new particles that do not possess the additional velocities due to contraction.

But do the particles of the vacuum react with each other? See page 2 of the storyline ELECTRIC NET FORCE IN REAL MATTER.