Do the charges of the vacuum react with each other?
To cover the range of QED we only regard here electric interactions between charged particles. For convenience we regard the particles as electrons and positrons. The wavy lines in the Feynman diagrams are photons then.
Electric charges are in kinds +
and -
.
- repels -, + repels +, - and + (and also + and -) attract each other, that's the attraction-repulsion law we use here.
Do the charges of the vacuum react with each other? We say at first approximation - zero order Feynman diagrams only (no photon couplings) - that the answer is no. When two virtual particles happen to appear in each others neighborhood at overlapping time intervals, they do not see each other. They live in different worlds. Those worlds interfere, as observed by the outside observer, but they do not react with each other.
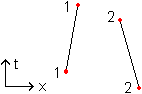
The picture is in fact two different Feynman diagrams in interference
| 1
2 Att: 0 Rep: 0 Net: 0 |
- - 0 0 0 |
- + 0 0 0 |
+ - 0 0 0 |
+ + 0 0 0 |
Att = number of attractions, Rep = number of repulsions, Net = net force.
It is not very surprising particles 1 and 2 do not see each other since the connecting photon between them is missing.
Each column gives one possible charge distribution of the involved particles (only 1 and 2 here). Electrons and positrons have equal chance to appear in the vacuum, therefore all possible charge distributions appear with equal chance, and not only the charge distributions with equal numbers of positive and negative charge.
The last three rows in the table count attractive and repulsive interactions. Net force
in the last row counts Attractive
minus Repulsive
which estimates the electric netforce in the charge distribution considered in this column. A positive number indicates a contracting netforce there, a negative number indicates an expanding netforce.
The next contributing possibilities are
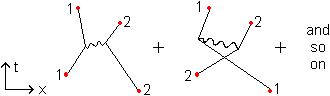
| 1
2 Att: 2 Rep: 2 Net: 0 |
- - 0 1 -1 |
- + 1 0 1 |
+ - 1 0 1 |
+ + 0 1 -1 |
Every time you add a photon-electron coupling to a diagram the amplitude of the wavefunction of that diagram diminishes by a factor of nearly 10. That is the value of the coupling constant of the electric force, the photon. Since the virtual photon is always emitted and absorbed, in the diagrams photon-electron couplings appear in pairs. So per added photon the wavefunction of the diagram diminishes in strength by a factor 100.
From the table above we infer that the chance of 1 and 2 being in a repelling interaction (they are both electrons or both positrons) equals the chance of 1 and 2 being in an attractive interaction (1 is an electron and 2 a positron; 2 is an electron and 1 a positron). So even when there are more particles in interaction, the interaction between every pair of particles in the cloud has a like chance to be repelling as to be attractive.
Every charged particle with antiparticle of same mass and opposite charge, appears positive or negative with like chance in the vacuum. (So yielding a zero electric netforce.) The electron and positron; muon and antimuon; W+ and W-; u-quark and anti-u-quark; proton and antiproton; pion and antipion; kaon and antikaon; and so on.
So there will be no electric netforce in the Feynman diagrams for electric charges in the vacuum. But maybe it is still worthwhile to follow what's happening in detail when one is estimating the electric netforce. Follow the green buttons of the QED
storyline.
But there is more than electromagnetism alone in the vacuum. Except for the photon we have the gluon and the W+, W- and Z-null bosons as force mediating particles. All the known particles contribute to the virtual vacuum, however some more than others. Follow the NETFORCE
grey buttons.