The sea of possibilities

A film play in reversed time direction
- The classical view

Event A := Event B here means Event A becomes Event B by means of time reversal. In this page time reversed means: the film of the event being played backwards. The event before the := always can exist physically with a reasonable chance of occurrence. If the reversed event after the := cannot exist or is very unlikely, the event is indicated by an arrow.

7) Suppose you have a hot chamber and a cold chamber against one another. In both chambers are molecules. The chamber contents are separated, molecules cannot go from one chamber to the other. Heat spreads through the walls. Suppose there is only heat exchange through the partition between the chambers, for convenience suppose the heat loss to the outside (as well as heat coming in from the outside) to be negligible.

Cold             Hot

First consider the heat in the hot chamber. Assume for the moment all the particles in the cold chamber being at zero temperature (almost), their heat content to be negligible. Observe how the heat of the hot chamber spreads over the other chamber. When both chambers have equal temperature all over, equilibrium (1) is achieved.

Now consider the heat in the cold chamber. Return to initial state and subsequently assume all the particles of the hot chamber being at almost zero temperature, containing negligible heat. Observe how the heat of the cold chamber spreads over the other chamber. When both chambers have equal temperature all over, equilibrium (2) is achieved. This is of course a lower temperature than in equilibrium (1).

Return to initial state. Observe how the heat of the cold chamber spreads at the same time as the heat of the hot chamber does. Both heat spreads are precisely as if the initial heat in the other chamber was absent. Finally the equilibrium heat of (1) + (2) is achieved. Heat is energy and energy is conserved, at each moment the lower heat and the higher heat just sum up.

Heat spreads like the waves on a water surface. The hotter heat as well as the lower heat spread and add. It is as if heat streams from hot to cold.

8) Consider a pond of arbitrary shape, its surface being perfectly still. Then somewhere in the pond during about one minute, a wave generator produces huge waves, but not that huge the waves top over. After the generator has stopped, the water surface can be assumed to host a complex wave pattern. If there is no loss of wave energy by friction or reflection (for convenience we assume so) the pattern will go on evolving for ever.

Suddenly a grid as large as the whole pond, made of square tubes as long as the depth of the pond, is fully put into the water. Now all the water is in the grid. The water in each tube has precisely the height it had in that location of the pond at the moment the grid was put in. The water cannot escape from a tube. The water has stopped waving, its complex wave pattern frozen, stored as it is in the grid. Next day, same time, the grid is suddenly removed in the way it had been placed there. The waves then keep on evolving as if there had been no one-day time delay.

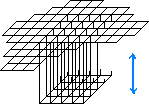
The grid, partly shown, goes through the water in the blue arrow direction.

(It has also been proposed to radar-image film the development of the water surface from above for about 20 minutes, then map out one image at the beginning, bring the surface to standstill by switching ON friction for a while, fill each tube of the grid with precisely enough water in accordance to the map and bring the flat bottom of the grid in touch with the silenced surface of the pond. Then release all tubes simultaneously while removing the grid quickly upward. Film the development of the water surface for 20 minutes and compare the two films. They should show identical course of events.)

This shows the following things.

 There is not really an impulse in the propagation of the wave. When the water was stored in the grid, all such impulses were rendered to zero. In fact there is not really a wave. There are only pillars of water side by side, spreading out over each other.

 Each pillar of water sags down and spreads out circular over the water around it, as if the other pillars were absent (principle of Huygens). They just spread out over each other. That’s all there is to a wave of water.

Is the spread of one such a pillar time reversible? Imagine a circular pond, its surface being perfectly still. Now in its center a regular series of waves is generated precisely until the first wave reaches the perimeter and then the generator stops. The whole pond now is covered with waves without overlap (no interference). When a wave spreads, its circle becomes larger and its height lowers. When the wave bounces of the perimeter, it reverses direction. The wave’s circle becomes smaller again, the wave crests heighten and when reaching the center they have precisely the energy with which they were created. They could give it all back to the generator. If not, the wave bounces elastically of the generator as if they had just been created and it starts all over again. Without friction or other energy losses, this would last forever.

1         2         3  

So the spread of a pillar of water is time reversible? Let us have a closer look at one wave’s cross section. Wave 1, in what direction will it go, left or right? Wave 1 is symmetrical, there is no preferred direction, it cannot choose. It will sag down and split in two waves going in both directions, see 2 and 3. There is no impulse in these two waves, they consist of pillars of water only. If they were symmetric too, they would also split into two waves. Thus they are not symmetric, they can’t be. The slope of the wave in the direction of movement is a little bit steeper than its rear, causing water to fall in the ravine there. The extra water present at the rear prevents water streaming back. This causes the wave to propagate.

Reversing the film of the propagation of a wave on a water surface yield a wave propagating in the direction of its gentle slope and this cannot exist. Well, it is not completely impossible, but up to the impossible, as is argued in the next paragraph. So yes, there is a time arrow in the propagation of water waves.

9) When things were spread out, to undo this, each piece has to go back along its route. However, usually the spread pieces spread further. Not necessary in smaller pieces; displacement holds as a kind of spread too. But there are so many directions to spread along and only one to reassemble, to undo the spread. Therefore the time reversed version of a spread usually shows an unlikely row of events. Far more unlikely (but not impossible) than its forward time counterpart. Everything that spreads, usually has a time arrow. Emitted light and sound, dust, waves of water, shock waves. All time arrows.

The increase of entropy is about the spread of heat, the spread of pieces, the spread of the number of occupied states over the number of possible states.

Well, that is, if you wait long enough, any system of finite energy in a finite volume will some fine day return arbitrary close to its original state (Liouville, Poincaré). It all are just states. Every state will return arbitrary close to any of the other possible states, only if you wait long enough.

Entropy is better taken as the number of arrangements of its constituents, the number of all its possible states, without referring to the actual state. Actually, entropy is taken to be proportional to the logarithm of the number of arrangements.

System A has n constituents, a second system B has m constituents, = is proportional to.

If the number of arrangements of A 2^n, then the entropy of A log ( 2^n ) n

Similar arrangements of B 2^m, entropy B log ( 2^m ) m

When two systems are joined, the number of arrangements in the joined system equals the product of the number of arrangements of the original systems. The entropy of the joined system equals the sum of the entropies of the original systems.

Usually the number of disordered states, with maximum applied spread, outnumber largely the number of ordered, unspread states. It is most likely to develop from an ordered state, with smaller number of similar states, to a state with larger number of comparable states, the disordered states. So disorder, or spread, increases. Entropy is increasing, as they call it. Mind this is not a law. It only is most probable entropy will increase.

Brian Green in his book The fabric of the cosmos points out that this means that an unlikely state like the world around you, most of the time is supposed to be preceded by a more unlikely state, which on its turn is preceded by a still more unlikely state, and so on - would you call this an explanation? Until in the uttermost distant past you have the unlikeliest state possible, and how likely is that to be, ever. Well, as said, every system of finite energy in a finite volume will some fine day return arbitrary close to its original state, if you only wait long enough. So all acquired entropy increase will some day spontaneously be undone to an arbitrary level of accuracy. Some day.

Read Brian Green, chapter Chance and the arrow.

10) Somewhere in the void between the galaxies there is a large cloud of atoms. They are all of the same kind, H2 or C-60 or anything. Deep in the cloud there are 14 atoms in each others neighborhood, see the red dots 1 up to 14 in the first picture. Atom 10 emits one photon in unknown direction. As experienced by us, Outside Observers, a spherical superposition of photons (one for every distinguishable direction) spreads with light speed from the atom. It passes by the atoms 9, 8, 7, 6, 5, 13, 4 and 3, one after another without being absorbed, and finally arrives at atom 14. There the photon is absorbed, just before the sphere would have reached 2 and 1. The photon is observed, the wavefunction collapses.

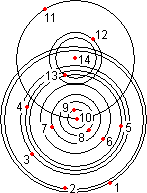
A photon going from 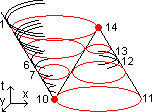atom 10 to atom 14

The forward propagation is as valid as the backward cone

The time reversed version of this course of events starts with a sphere of photon superpositions (through 14 and between the spheres of 2 and 3 in the picture) suddenly emerging in space and then shrinking down, back to the atom it came from (atom 10) and subsequently become absorbed there.

On itself this is not forbidden but in forward time space such superposition fronts don’t occur this way. But wait, superposition shells cannot be observed. In this case the superposition is superposed by another superposition, unobservable either: the spherical superposition of photons spreading with light speed from atom 14. Mind this evolution is backward in time. But this superposition has a different evolution! It subsequently passes by atoms 13, 12 and 9 before simultaneously arriving at 10 and 11. It misses 4 absorption chances and is then absorbed by atom 10. But hey! the chance to skip 4 chances is larger than the chance to skip 8 chances of absorption! This means we have mistaken prevalent time direction: when a real photon is connecting atoms 10 and 14, then the chance the backward version occurs is larger than the chance to meet the forward version. One could conclude time runs backward there. (Maybe this item nr 10 is not so classic after all.)

The photon connects atoms 10 and 14. The superposed photon-spheres from emission to absorption, forward as well as backward in time, are unobserved. As far as concerned the basic actions in QED the backward time course of events is as valid as the forward time course.

In the picture at the right are shown four moments. There t is the normal, forward time. At each moment the photon shells forward and backward shown in one horizontal plane should contribute to the wavefunction of the photon between 10 an 14. 1) atom 10 at moment of emission plus the photon shell through 10 and 11; 2) a smaller red circle in a second horizontal plane plus the neighboring smaller red circle in the other cone; 3) in a third horizontal plane, summed another two such circles, having interchanges size more or less; 4) the photon shell between the spheres of 2 and 3 through 14 plus 14 at its moment of emission backward in time.

The version containing backward time contributions has different statistics than the version consisting of forward time contributions only. In principle it is calculable and the outcome of experiment then should decide. So far this is ordinary quantum mechanics.

To be fair, QED renormalization calculates the sum of all possible ways through all of spacetime the photon could have traveled from 10 to 14. All possible ways from 14 back to 10 are not added in QED renormalization. Nevertheless, QED works perfect without the backward version. I guess it has never been tried, adding the backward version in QED, but I think, since the coupling has no time arrow, there should have been a backward contribution in QED.

Unless there is time arrow in the vacuum itself, spoiling the superposition. If backward time vacuum is distinguishable from forward time vacuum then they will not superpose. A choice out of the two of them, forward and backward, will be made.

Well then, is there a time arrow in the cloud? If forward time vacuum and backward time vacuum are indistinguishable: no, there isn’t. I mean, yes, there is, but only local and shortliving and supposed to occur in equal amounts forward and backward. There is a cloud of atoms and photons rushing between them, but a large scale time arrow is absent. That is, deep inside the cloud. But the border of the cloud emits the heat radiation fitting to the cloud’s temperature into the void.

To be continued at the next page.