Experiment 4 - the experiment

Description

The main idea of page 2 the storyline THE COLLAPSE OF THE WAVEFUNCTION can be stated as follows:

For every observer W1 who by means of an observation P (by example one photon) does make collapse the wavefunction of a system E (by example an electron), there can be found an other observer W2 for whom the wavefunction of W1 + P + E hasn’t collapsed.

In the probability distribution of this wavefunction (W1 + P + E) the observation P of E by W1 doesn’t exist. It does as wavefunction, but not as an observation.

I tried to shape this in an experiment. It starts as in the famous experiment with the Cat of Schrödinger. Then it runs into the equally famous two slit experiment. Finally a second and a third observer enters the scene.

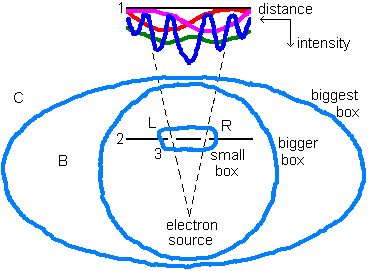
The blue rectangle, the circle and the ellipse represent boxes like that where the Cat of Schrödinger was put in. The nanorobot A is just outside the small box.

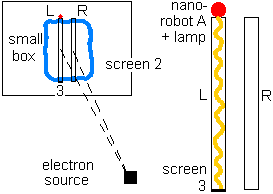
A is a nanorobot (the red dot) that resides within screen 2, just above the L-slit (the left slit in screen 2). In nanorobot A is a radioactive atom. When the atom decays, the robot turns on a lamp (instead of killing a cat by poison). Nanorobot A has at its disposal the readings from screens 1, 2 and 3.

Clicking these two pictures is meant to open two pop-up screens with the same pictures. With these two figures at hand the rest of the page is easier to follow.

When the atom has not yet decayed nothing happens and the lamp remains off. When one half-life of the atom has passed by the atom is in a superposition of even amounts of decayed as not-decayed. At that moment the connection between the radioactive atom and the lamp is shut of. The as yet decaying of the atom will not turn on the lamp no more.

Dotted lines = electrons, fired off one by one in such a way there is always only one electron in motion present in the experiment.
The electron-source is directed to the middle point of the slits. The indeterminacy of the electrons makes it sometimes go through the L-slit, sometimes through the R-slit, but in most cases to end in screen 2.

= screenmaterial.
Screen 1 detects location of electron-hits that has passed screen 2.
Screen 2 detects and shields away electron-hits who thus had missed the two slits that are present in screen 2.
Screen 3 resides at the bottom of the L-slit and detects the photon from the lamp.

= photons, fired off by the lamp one by one. For every electron emitted by the electron source the lamp fires off one photon. The photon crosses the length of the L-slit and is detected by screen 3 at the bottom of the L-slit. The timing is such that an electron going through the L-slit and the current photon from the lamp will always hit each other. The photon doesn’t disturb the electrons path but in the collision the photon itself is scattered away. The pattern of electron-hits appearing on screen 1 should not be disturbed by collision-effects of the photon and the electron. When the photon is scattered away this is confirmed by the absence of a screen-3-hit. On the other hand a photon-hit on screen 3 is interpreted as the electron not passing the L-slit.

As long as there is no observation with the photon-lamp the individual electrons go simultaneous through both slits and are projected then on screen 1. There the interference pattern of darker and lighter bands appears.

For the electron to follow its path undisturbed, the photon must be not too energetic. But too low energetic photons don’t interact with the electron certainly enough, don’t they? Maybe it is necessary to prepare all the photons at spin -1 and all the electrons at spin +1/2 and to align the spin-axis of the electrons and photons on forehand. This enlarges the chance on a reaction between them to its maximum. The machinery for this can reside outside all boxes since they might be too big. So the photon always comes from the outside. The act of switching on the lamp might be the opening of a shutter at the top of the L-slit to let the photon to pass by. Once opened the shutter remains open. Should that do? When there is a meting of the particles we must be able to trust the reaction will take place. And we want to detect every fired electron, in screen 2 or in screen 1. We don’t want to loose an electron because it was diverted by the photon collision. We must be able to trust on that too. Can this be done?

The experiment takes off

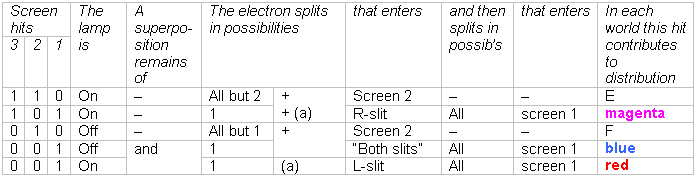
Assume the radioactive atom in A did not decay in time and the lamp is off. The shutter is closed and screen 3 detects nothing. An electron is fired off. The nanorobot A splits in a large number of worlds. In all of them except for one A registers a measurement somewhere in screen 2: the electron has missed the slits. In every of those worlds this is supported by the absence of an electron-hit on screen 1. In the one exceptional world A does not measure an electron-hit in screen 2 and we draw the conclusion it has passed the slits which is confirmed by an electron-hit on screen 1.

The nanorobot doesn’t know through which slit the electron went. The small box is closed, its content being in a superposition of its two states (electron passes through the L-slit; electron passes through the R-slit). After a number of screen-1-hits A begins to distinguish the blue distribution of light and dark bands of the interference pattern from the electrons coming through the slits.

After a large number of releases there is one world where all the electrons hit screen 2. There must be one world where they all went both slits. The chance is the biggest to found oneself back in a world where nearly all electrons end up in screen 2 and the remaining fraction go both slits.

Assume the radioactive atom in A did decay in time and the lamp is on. The shutter is open. An electron is fired off. Nanorobot A splits in a large number of worlds. In all of them except for two A registers a measurement somewhere in screen 2: the electron has missed the slits. In every of those worlds there is a photon-detection on screen 3 and the absence of an electron-hit on screen 1. But there are two worlds left in which the electron passed the slits and where A knows through which one. The small box is opened there.

In one world A registers the absence of a photon-hit on screen 3, the absence of an electron-hit on screen 2 and an electron-hit on screen 1. Therefore A concludes the electron has passed the L-slit and has scattered the photon away. In the other world A registers a photon-hit on screen 3, the absence of an electron-hit on screen 2 and an electron-hit on screen 1. There A concludes the electron has passed through the R-slit. After a number of screen-1-hits A begins to distinguish the red distribution from the electrons that went through the L slit plus the magenta distribution from the electrons that went through the R slit. This is the green distribution.

After a large number of releases there is one world where all the electrons hit screen 2. There must be one world where they all went through the L-slit. And another one where they all went through the R-slit. In most cases it is something in between. The chance is the biggest to be in a world where nearly all electrons end up in screen 2 and from the remaining part approximately half of the electrons go L and half of them go R in some random alternation.

A human being enters the scene

B is a human Being that has no access to what is in the bigger box (see figure) except for that B sees the records of screen 1, 2 and 3. A hit on one of those screens is an observation done by B making the world of B to split in all its possibilities, all the possible places where the hit can occur.

How soon B will be hit by decoherence which opens the bigger box? How small must A be made to slow down decoherence sufficiently for B to finish the experiment? Would it make sense to make A of one radioactive atom, putted in a C60-buckyball and connecting the ball to the shutter by a carbon nanotube? The purpose is the radioactive atom decays, the decay-products hit the carbon cage and release some electrons there, which subsequently runs through the carbon tube to the shutter and switch it open. Does the C60 survive such a decay not too damaged?
Let’s assume for now the nanorobot A at least consists of one radioactive atom, a C60-buckyball, a nanotube, some electric circuiting, a shutter and a memory.
Will the circuit work reliable? Too small circuits suffer of quantum uncertainty. Can the shutter work reliable enough? The lamp must be able to be in a definite state on or off.
In fact, A is an experiment on its own.

When B registers a photon-hit on screen 3, B has entered the world in which the radioactive atom has decayed in time. The shutter is open, the lamp is on. The bigger box has been opened. The electron that is fired off along with the photon is most likely to hit screen 2. The chance is low it precisely aimed for one of the slits. So the electron splits in all the electrons ending in all the possible places of screen 2 and one electron that is passing through the R-slit and one electron that is passing through the L-slit (the latter one without screen-3-hit, see more about this 2 paragraphs ahead). Each of these two electrons then splits in all the electrons hitting all the possible places of screen 1. Always remember, these are all different worlds that do not see each other. The R-slit-electron contributes to a magenta distribution while the L-slit-electron contributes to a red distribution.

When an electron has been fired off and B has not registered a photon on screen 3 then the lamp is off (except for the case in the next paragraph). The electron splits in all the electrons ending in all the possible places of screen 2 and one electron passing both slits simultaneously. This last world splits in the all the electrons hitting all the possible places of screen 1, each hit contributing to a blue distribution on screen 1.

The absence of a screen-3-hit is not completely decisive about the lamp being off. If the radioactive atom decayed in time the lamp is on. Suppose a photon is fired off and the electron went through the L-slit, scatters away the photon and splits in all the electrons hitting all the possible places of screen 1 contributing to a red distribution. Then the lamp is on without a screen-3-hit.

An overview of this is presented in the next table.

We have five different endstates, from which four are distinguishable.

A next electron is fired off in each of the possible worlds. It ends most likely in screen 2. If not yet decided whether the lamp is on or off it is now, so can be expected. With only a few screen-1 electron-hits a pattern cannot be distinguished there yet. Once the state of the lamp is decided one only comes across the green lamp-on distribution on screen 1 or the blue lamp-off distribution.

When there are fired more and more electrons, there must be one world in which the lamp is on and all the electrons go L. And one world in which the lamp is off and all the electrons go through both slits. If so then B observes these two possibilities to remain in superposition for ever, leaving the lamp on and off at the same time. But it is most unlikely B finds itself back in such a world. A screen-2-hit is decisive whether the lamp is on or of, so the first screen-2-hit will be decisive on that. A screen-2 electron-hit with absent screen-3 photon-hit (all F-worlds) is a detection the lamp is off and in all those worlds the lamp remains off. A screen-2 electron-hit plus a screen-3 photon-hit (all E-worlds) is a detection the lamp is on and then the lamp remains on.

When all electrons go R the accompanying screen-3-hits reveal the lamp is on. When all electrons go screen 2 we haven’t entered a very interesting world, isn’t it? But this is all most unlikely. After quite a number of hits necessary for a pattern to appear on screen 1, it is the most probable B finds itself back in a world where the lamp is on or in a world where the lamp is off.

So we better put screen 2 and screen 3 in the bigger box too, as in fact the figure is indicating. (Technically it is difficult to draw screen 2 outside the bigger box. We are in three dimensions, screen 3 is at the bottom of a slit and A at the top so it can be done for screen 3.) But we shall provide the screens 2 and 3 with a memory that stores when hit. Then the screen-2- and screen-3-observations lay there for anyone willing to look at it on a later time. Anyway, nanorobot A will always have those measurement-results too. We can always ask A.

Suppose B manages sufficiently to shield away decoherence effects from screen 3 and especially screen 2. When we have no access to screen-2- or screen-3-measurements we can only draw the superpositions of all possible cases. What are those?

After some time quite a number of particle releases have taken place. When we discard in our minds all cases of screen-2-hits, in half of all remaining cases B expects to find no hits on screen 3 because the lamp was off. (As should become evident when B checks the memory of screen 2 and 3 afterward, or asked A. We need to check screen-2-hits to be able to discard them.). When the lamp was on B expects half of those cases no photon-hits too because the photon has been scattered away by the electron passing the L-slit. In the remaining half, and so only one quarter of all non-screen-2-hit-cases, B indeed expects to find a record of a photon-hit on screen 3. So what does B draw as the state of the memory of screen 2 or 3 or A when checked?

B experiences the interference effects (if any) of the wavefunction of the material of an A-memory that stores no hits on screen 3 with the wavefunction of the material of an A-memory that stores screen-3-hits in half of all cases. When we discard all screen-2-hits those two sets of wavefunctions have equal strength. The same holds for the screen-2- and screen-3-memories. B cannot verify this. At the moment B would try so by making contact with screen 2, 3 or A the wavefunction of what is in the bigger box collapses and the state of the memory of screen 3 changes into OR no detections (lamp off) OR detections in half of all observations (lamp on), when discarded all screen-2-hits. In accordance with page 2 and 3 in the storyline THE SEA OF POSSIBILITIES the reality of screen 2, 3 and A has adapted itself to the reality of B. That is, in fact the reality of B is adapting itself to one of the superposed possibilities. But since B cannot know the reality of screen 2, 3 or A before the act of making contact, B will not notice this change.

As far as I can see the detection of screen 1 doesn’t have this disadvantage. An electron can have travelled from the electron source on to a certain point on screen 1 via one of the slits while there was an observation by a photon from the photon lamp in A, as well as that this happened while the lamp was off. As far as I can see this are undistinguishable alternatives for B and so there is interference of these alternatives - that is, as long as decoherence effects are small enough to keep A, the photons, screens 2 (with the slits), screen 3 and the electrons inside the bigger box.

Once again regard the moment B is making contact with A. The bigger box opens en the superposition of A collapses. For B the lamp now is on or off, but not both.

When the lamp is on the interference pattern on screen 1, being red + magenta + blue now changes into red + magenta (which is the green pattern). Screen 3 shows detections in half of all screen-1-hit measurements.

When the lamp is off the interference pattern on screen 1, being red + magenta + blue now changes into blue. Screen 3 shows no detections at all.

And this is a shocking conclusion! The physical present divisions on screen 1 alter in other, different physical present divisions!

I must have made a mistake somewhere. The observation of the red + magenta + blue division should not occur since it holds as a measurement. From the beginning there must already have been made a choice whether the lamp is on or off. One sees red + magenta on screen 1 when the lamp is on and blue when the lamp is off. It should be impossible for B to keep A in the bigger box. But I don’t see why. Decoherence is not a fundamental feature of spacetime. Except from the uncertainty relations of Heisenberg decoherence in principle can be made as small as desired. Then all superpositions remain intact that lead to the red + magenta + blue division.

Let’s assume the red + magenta + blue division does occur and see what happen.

Only by making contact with the nanorobot A, for B the superposition on screen 1 change observably. It is the reality of B itself that changes! At that moment B has conveyed from someone standing outside the situation and observing a superposition of all possibilities, to someone that is part of the situation and has plunged in one of the superposed states. But which one?

A second human being enters the scene

There is a person C for whom A, B, the electrons and the photons are present in a biggest box (see figure). This C has established decoherence effects to be slowed down sufficiently to perform the experiment. He (assume it’s a he) has no contact whatsoever with the contents of the biggest box except for he gets readings from screen 1. Then C sees on screen 1 the sum of the distributions red + magenta + blue. That’s precisely the same as B saw before opening the bigger box by making contact with A. But now B is part of one of the superposed possibilities. But which one?

I think no choice is made. C sees the lamp is on and off at the same time. But I suspect B - that is the B making contact with A - is present in both states, in the one in which the lamp is on as well as the one wherein the lamp is off. That is to say, as observed by C both states exist and B cannot disappear just like that. Even not from one of the possibilities that, as later B can assure to C if C would ask for, has a reality experience of its own.

There must exist two B’s, as observed from C. One in each of the possible states of lamp-on or lamp-off. And each B has its own experience of reality. B itself doesn’t notice anything of this. None of the B’s. And each reality experience has an own A. So there are two A’s too. And as soon as C makes contact with B henceforward there are also two C’s. And so on. Each time you make a wavefunction collapse and measure a certain value, there are other you’s at the same time and place that measured the other possible values.

And then the contact between A and B is disconnected again. What happens then? When in the two-slit experiment measurement is stopped the interference pattern reappears on the screen behind the slits. But that is then with new electrons!

Now there are two A-and-B’s. One of them has a radioactive atom that has decayed and then it remains decayed. In this case there isn’t a new radioactive atom, isn’t it? The other A-and-B has a radioactive atom that hasn’t decayed. And I think with that one the whole experiment as described so far can start over again.
It seems there is always one possibility left where the radioactive atom hasn’t decayed. This resembles the quantum-Zeno-effect in which a state 1, that in a certain time shifts to another state 2, cannot do this because there is measurement all the time setting the just started shifting back to state 1.

The state you observe depends on your point off view. Things look pretty different from inside a box than as observed from the outside.

But arguing backward in time from screen 1 onto the radioactive atom things seem to look different. Suppose, only the blue pattern is visible on screen 1. Then we are in the possibility where we have made an observation the lamp is off and the radioactive atom didn’t decay in that first elapse of time at the length of one half-life. But reasoning in forward time-direction the experiment consists of a superposition of an increasing number of states with each its own experience of reality. So when you are in one of those states with an own reality experience and then reason back along the course of the experiment, then you have to meet somewhere the other realities and go in superposition with them. The state with the atom not decaying superpose with the one in which it does decay. But you will never notice that. In our reality experience the atom hasn’t decayed in time and the lamp is off and we see the blue distribution on screen 1. The other realities that are superposed with us we don’t see no longer. Unless there happens something strange as described for the forward time direction, like the red + magenta + blue changing into blue. When going backward in time one would actually see appearing from the nothing the other states and superpose with them, united again.

2006-02-27 first edition

2007-11-09 second edition

NDER    LONG TERM  ONSTRUCTION