Experiment 1 - the EPR experiment
Near to earth a correlated pair of photons emerges from a source. Photon 1 goes this way; photon 2 goes the opposite direction. The photons are in a superposition of the states “photon 1 has spin up and photon 2 has spin down” and “photon 2 spin up and photon 1 spin down”. After one hour photon 1 hits a probe and its spin is measured to be “up”. What about the superposition? What about the spin of photon 2?
p1 <---------------- source ------------------> p2
According to The story and The story - part 2
at page 2 of the storyline THE COLLAPSE OF THE WAVEFUNCTION, there are two complete worlds existing, occupying the same space at the same time. In world 1 photon 1 has spin up and photon 2 has spin down. Denote this as w1 = p1 + p2
+ p2 . In world 2 photon 2 has spin up and photon 1 has spin down, w2 = p2
. In world 2 photon 2 has spin up and photon 1 has spin down, w2 = p2 + p1
+ p1 . When the probe measures the spin it splits into two identical versions at the same place and at the same time. One version of the probe enters world 1. The other version enters world 2, measuring our photon to have spin down.
. When the probe measures the spin it splits into two identical versions at the same place and at the same time. One version of the probe enters world 1. The other version enters world 2, measuring our photon to have spin down.
Within a couple of hours after entering, decoherence provides the rest of the solar system having entered the two worlds too.
There is no spooky action on a distance
. The only unbelievable thing is the existence of alternatives of the current situation at the same time and the same place. Complete solar systems, at least. But we have to believe since we remember having measured in an earlier stage the interference pattern of both worlds pervading each other. And in principle there are others far away, Outside Observers not yet hit by decoherence, who still measure the interference pattern of the superposition of the worlds from which we have already entered one.
Let's once again return to our world where the probe has measured p1 to be up. The probe has measured spin up, so that possibility is real. The Outside Observers observe the interference of w1 and w2 and see no clue whatsoever that one of that worlds is more real than the other. Therefore the Outside Observers judge w1 and w2 as equally real. And since we know that one of those worlds is real, the other one must be real too.
So w1 and w2 are real. The environment of one of them, the rest of the world around the two photons of e.g. w1, is real when it includes you, as you can see. But the reality of the identical environment around the two photons of w2 is a believe. We have no measurements from that second identical world. Therefore quantum mechanics demands that superposing with one identical environment around w2 are all other possible environments that also could have sustained the two unobserved photons of w2 at that moment. It is more than only two worlds existing at the same place and time. I cannot estimate how large a mistake we make by ignoring all of the superposing worlds except for the one that is identical to ours. In this site the mistake is taken to be that small we can ignore it.
This experiment is at every moment entirely described by four points on a straight line (except for the starting moment). All nearby points have constant relative velocity of 2/3 * c, where c = the speed of light. All points start out from one point (one space time event), although the two laboratories  and
and  can be thought of having had the same velocity before that.
can be thought of having had the same velocity before that.
The experiment consists of two EPR-experiments combined simultaneous:
 <--- 2/3 c <--- 2/3 c
| 
| 2/3 c ---> 
|
| (1)
|
and
|
|
| 
| 2/3 c ---> 
| 2/3 c --->> 
| (2)
|
ad up to the experiment
|
 <--- 2/3 c <--- 2/3 c
|  
| 2/3 c --->  
| 2/3 c --->> 
| (3)
|
In experiment (1) the particles  and
and  are a correlated electron-positron pair, created at an “2 photon
are a correlated electron-positron pair, created at an “2 photon  e+ e-” event in
e+ e-” event in  lab 1. And so are the
lab 1. And so are the  and
and  created at
created at  lab 2 in experiment (2)
lab 2 in experiment (2)
For the velocity of the uttermost right black particle, as observed in the lab 1 frame, we used the formula
(v1 + v2) / (1 + v1*v2/c )
)
= (2/3*c + 2/3*c) / (1 + 2/3*c*2/3*c / c )
)
= 0.923 * c
Because its resemblance with the simplest form of an expanding space, this should learn us something about correlated points in the expanding universe. But we don‘t go into that here.
The black particles are measured by a there already present satellite, or by a send-along instrument.
In the grey area with edge parallel to the x-axis, the spins of the correlated pair of particles of lab 1 are in a superposition of “ up +
up +  down” and “
down” and “ down +
down +  up”, according to usual EPR requirements. Above that edge the wavefunction has collapsed to either
up”, according to usual EPR requirements. Above that edge the wavefunction has collapsed to either  up and
up and  down or the other way around. In the other grey area with edge parallel to the x'-axis the correlated particles of lab 2 are also in superposition of spin up-down and down-up. Above that edge the wavefunction has also collapsed to either
down or the other way around. In the other grey area with edge parallel to the x'-axis the correlated particles of lab 2 are also in superposition of spin up-down and down-up. Above that edge the wavefunction has also collapsed to either  up and
up and  down or vice versa.
down or vice versa.
Which edge is the true one? The situation with respect to lab 1 and lab 2 and their correlated particles is completely symmetric. Both grey areas are equally valid and so it seems both areas are simultaneously present. Oke, so be it, for the unobserved superpositions. But when spins are measured and results are send with light speed to lab 1 and lab 2, one can see in the picture that both labs receive their messages simultaneously. Leaving no space for any eventually contradictional behavior.
The picture is a Minkowski diagram made in lab 1, it is a lab-1 recording. Because of the symmetry of the situation the Minkowski diagram as observed from lab 2 must be precisely the same. Except, maybe, for the picture being left-right mirror reflected.
What if, at the creation of the two pairs of particles, the particles somehow got mixed up? E.g. one has lost track accidentally which positron belongs to which laboratory exactly. How can one distinguish? CAN one distinguish? Different pair divisions can give different wavefunction collapse edges in spacetime. Well, you know the quantum rule: as long as the possibilities cannot be distinguished, they go in superposition. Maybe I should have used an e+ e- pair for lab 1 and a p+ p- pair for lab 2.
EPR in GR
When one of the particles in the EPR experiment falls in a black hole, its signal cannot reach out to us anymore. How this works out precisely depends on in how far the routes of particles in renormalization procedure follow the gravitational curves of spacetime. See Renormalization at page 4 of THE COLLAPSE OF THE WAVEFUNCTION.
 + p2
+ p2 . In world 2 photon 2 has spin up and photon 1 has spin down, w2 = p2
. In world 2 photon 2 has spin up and photon 1 has spin down, w2 = p2 + p1
+ p1 . When the probe measures the spin it splits into two identical versions at the same place and at the same time. One version of the probe enters world 1. The other version enters world 2, measuring our photon to have spin down.
. When the probe measures the spin it splits into two identical versions at the same place and at the same time. One version of the probe enters world 1. The other version enters world 2, measuring our photon to have spin down.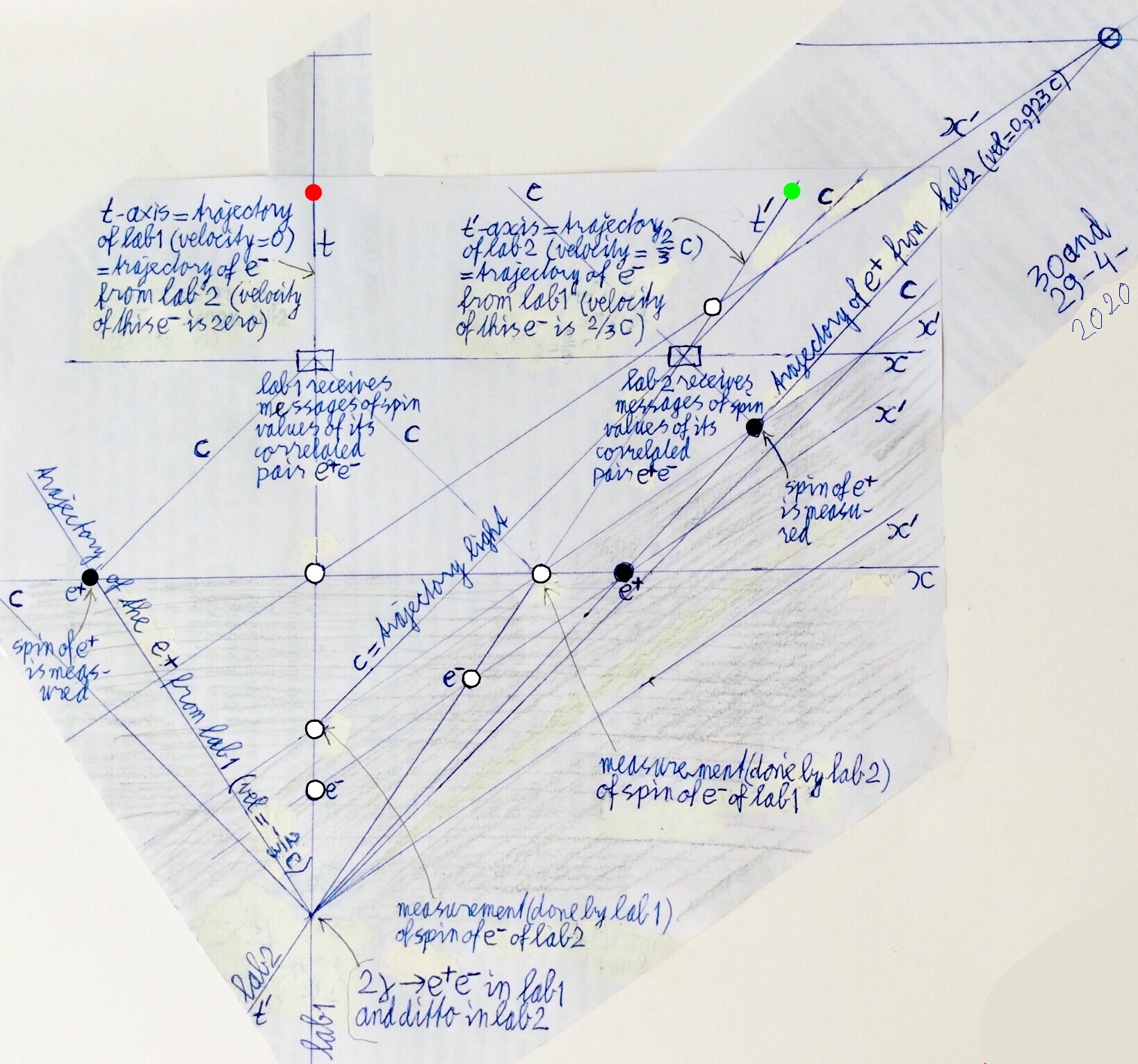
 and
and  can be thought of having had the same velocity before that.
can be thought of having had the same velocity before that. <--- 2/3 c
<--- 2/3 c

 e+ e-” event in
e+ e-” event in  )
)