Chapter 3
Quantum Quaternion Dynamics
I ran into the existence of quaternions in 2012. In QCD there are three colors of the strong force and together they form something that has no color no more and that is called white. There are three imaginary quaternion units and multiplied together they form something that has no imaginarity no more: ijk = -1 or kji = 1. It was this resemblance that stroke me in 2012 and put me on the track.
Abstract 
Page 31
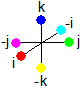
Quaternions are defined by: i
= j = k = ijk = -1
Colors as Quaternions:
= 1, 
= i, 
= j, 
= k, 
= -1, 
= -i, 
= -j, 
= -k
Gluons: 
= / = -j / -i = i * -j = -k =
Page 32
Two colors together: in the Feynman diagram. We RIGHT MULTIPLY the quark by the gluon. In a reaction equation involving emission and absorption of a gluon of color k (take the color of the gluon to be k) the k has to be assigned to the coupling. Then there appears one k at both ends of the gluon.
Page 33
About 3 colors applied together. When particles couple and merge to a merger particle, the colors (quaternion units) of the particles must be multiplied.
Regardless the colored outcome, the observed color product end state always is +1 or -1.
When the particles stay together but do not merge, their colors sum up. All possible multiplication orders superpose, so then the sum end state of a color composition (colors not merging) is always zero.
The physical interpretation of multiplication order is: start multiplying with this, a little later with that and at last with this. And something about mesons.
Quarks have color and antiquarks have anticolor
After the black bar: 1) Some worked out color reactions. 2) Three gluons applied together,
which is about the glu3on, a composition of 3 gluons together without immediately merging. 3) And a previous attempt.
Page 34
The CPT theorem applies to colors in quaternions. Colors are imaginary in QQD. Colorless end state is compulsory for us, Outside Observers, without any imaginary component. There is a real-imaginary swap working when going from 1ijk colorspace to xyzt spacetime, and vice versa. About color -1.
Page 35
Allow the Minus Sign Go Wild approach and start with a population of well-known baryon colors (i + j + k per baryon). By black glueball exchange one soon ends up with a population of mainly baryons like *-i *-j *k which are colored states. The ratio of plus-color abundance to minus-color abundance then is 1 : 2 or 1/3 : 2/3.
Page 36
Quaternions as 2 x 2 matrices. When two Pauli matrices are multiplied, one always obtains a quaternion unit matrix - all the quaternion units except for -1. Quaternions are SU(2). Resemblances and differences between QQD and QCD.
