A second free falling system, moving with a velocity with respect to the first system

We continue our effort to transform away the Newton gravitational field in an Einsteinian way of thinking.

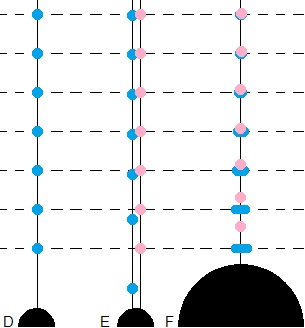              Fig. 3

D is at startmoment 1, E and F are at moment 2.
E is the system of rods and clocks, F is the system of free falling clocks.

Now imagine an endless row of clocks along a radius from the center of Earth. Every blue ball is a clock of one unit of length diameter. At start state D every clock has same distance to its two nearest clocks as measured with clock diameters, forming an endless ruler perpendicular to the Earth surface. Our ruler starts infinite far away and ends at the Earth surface.

After a certain time the ruler in the system of rods and clocks looks like in E: not a usual ruler no more, nor an exponential ruler, but well, still a ruler of some kind. In the free falling system of F it was a ruler and so it is still the same ruler. Only the blue masses do spread in horizontal direction (parallel to the Earth surface), keeping their horizontal diameter at same ratio to the Earth diameter, and shrink in vertical direction (that is: along a radius from the Earth center).

At moment 2 in the system of rods and clocks E, we start a new ruler of pink masses standing still with respect to the Earth center. The ruler in fact is a copy of the ruler of blue masses at its start moment in D. Since the blue masses have build up some velocity and since the pink masses are standing still with respect to the Earth center, the blue masses pass by the pink masses. In F the motion of the blue masses is transformed away. Therefore in F the pink masses fall upward.

In the system of rods and clocks E, when two masses like a blue mass and its corresponding pink one, have a certain relative vertical velocity, they maintain that relative velocity while falling to the Earth. Also in the system of free falling clocks F the pink balls have constant velocity as measured in local blue ball vertical diameters. This is as it should be when gravitation is transformed away: there is no gravitation anymore and thus present velocities remain constant (first Newton law).

But no, this is not true. It is true only when the gravitational field is homogeneous, for environments where the gravitational field strength doesn't differ from place to place. The gravitational field of Earth in fact does not host such an environment. It is nearly true for balls near to each other, or far away from the Earth. In the system of rods and clocks a blue ball is always ahead on its corresponding pink ball on their way to the Earth surface. Therefore the blue ball constantly is in a little stronger field where the corresponding pink ball not yet has arrived. The blue ball undergoes an extra pull enlarging their relative velocity a tiny bit. The blue ball and the corresponding pink ball are in acceleration relative to each other. And even that acceleration is not a constant.

Imagine launching a temporarily ruler of red clocks (not shown). Not an endless row but say only 10 clocks long and initially coinciding with 10 subsequent pink balls. The red clocks are supplied by small rocket motors. Suppose, we are in the system of rods and clocks E. Now the motors are used to give the red balls just that extra push towards the Earth, needed to keep the velocity relative to its corresponding blue ball at constant. Soon the red balls separate from their pink balls. Since such a separation is an event, happening at one specific point in spacetime, also in the system of free falling clocks F the red and blue balls separate. In F the red balls have constant velocity as measured in local blue ball vertical diameters. And since the pink balls separate from the red balls, the pink balls do not have constant velocity, measured in local blue ball vertical diameters.

So gravitation has not been transformed away. It had for one system of rods and clocks only. But not for a simultaneous second system of rods and clocks that is in motion relative to the first.