Transforming away the Earth gravitational field

They say: gravitation can be transformed away. They say when you perform all your measurements with respect to a coordinate system that completely falls along with gravitation, in space as well as in time, then there is no way no more to measure or to detect gravitation. I tried to visualize this with some masses in the Earth gravitational field and taking into account tidal effects.

The idea seems so simple. You hang in outer space, in your space suit, motionless with respect to the Earth and 10,000 km above its surface (for convenience we set the rotation and speed of the Earth at zero). There is no gravitation and so you don't fall towards the Earth. Instead the Earth below you grows with an accelerated expansion. Also you grow at same expansion rate, so you and the Earth keep same ratio. Key is you and the Earth keep standing still, that is, the mass centers of you and the Earth keep standing still.

On Earth everything falls with same acceleration and when starting at stand still the covered distance of a falling object after t seconds is 4.9 * t meters. To mimic this the Earth surface has to cover that distance by growing. It is not an exponential growing like doubling every second would be. Doubling every second is 2^t but it is t^2.

You see the Earth growing and after an hour or so the Earth has grown that much its surface hits you. You almost instantly acquire the speed of the Earth surface - for convenience we assume you survive the impact well. Since the Earth keeps on to accelerate its growth, you will keep on feeling to be pushed onto the Earth surface. This is your weight. You stand up and jump. For a short time you move away from the Earth but soon the ever accelerating expansion of the Earth has caught up with you and pushes you to its surface just as before.

1) When repeating this on the moon, with an astronaut hanging still 1000 km above its surface, the moon and the astronaut will grow at lower acceleration than the Earth and its Earth bound companion. So whenever the astronauts would meet, their size ratio might differ astronomical.

2) There also is a problem with satellites. Since there is no gravitation to keep a satellite in orbit, you can imagine a satellite just moving at constant speed along a straight line. That straight line is parallel to the Earth surface and at the height of its orbit. It passes over way above the ground and when moving further on the straight line, the satellite tries to recede from Earth. But instead of building up mutual distance, the Earth grows in such a pace the distance from the satellite to the Earth surface remains the same. At first instant the satellite seems to orbit Earth, but after some time becomes apparent the satellite will never pass a certain point. The satellite will circumvent about one quarter of the planet once but never more.

Transforming away the Newtonian gravitational field

Let's try another approach. We try to transform away the Newton gravitational field in an Einsteinian way of thinking.

We start with the rigid system of rods and clocks from fig. 1 at page 1 of SR and then we decouple and remove all rods, leaving us with a system of free falling clocks. The small cubes at the intersecting places of the rods are the clocks. We distort the orthogonal coordinate system a little to get a polar coordinate system with the Origin in the center of the Earth. We focus on 6 clocks 10,000 km above the Earth surface. The clocks are transparent so light rays are allowed to proceed to the center of a clock, being reflected there and leave the clock again in a different direction. The clock cube ribs are one unit of length (not necessarily one meter). In the pictures the clocks are represented by small blue balls. We consider only one kind of force, gravitation. Without that force there would be no force working on the balls.

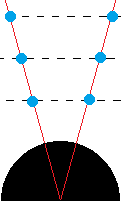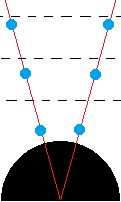A             B             C 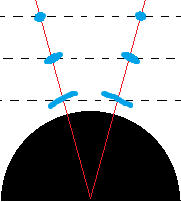            Fig. 1

A is the start state at moment 1; B and C are end states at moment 2, some time later. Not on scale.

Regard B, the end state as it would have been observed in the system of rods and clocks. This is the well known picture. Balls next to each other in horizontal direction (parallel to the Earth surface) that have fallen half the distance to the center of the Earth are twice as near to each other now, because every ball falls to the center of the Earth. Balls above each other (on a radius from the center of the Earth) will have increased mutual distance. Balls above each other higher above the Earth surface have built up lesser increase of mutual distance than lower balls above each other, because gravitation is stronger when nearer to the Earth. These distortions of a block-like volume, when falling to the Earth, are called tidal effects.

Now regard C, the system of free falling clocks. There is no gravitation observed there. The system of clocks falls such that every clock is weightless in its fall down to Earth. Clocks don't observe gravitation no more, so there is no gravitation no more. As a consequence clocks that are standing still relative to each other, and to the center of the Earth, keep standing still to each other and to the center of the Earth. And every two clocks that were running same time at same pace keep running the same time and pace.

Light rays going from one ball center to the other, or from one ball center to the center of the Earth, should always need the same amount of time to cover this distance.

Instead the Earth expands. And the blue balls elongate horizontally. The unit length embodied by the clock's horizontal diameter elongates parallel to the Earth surface. Lower balls have horizontal meter sticks that are more elongated than upper balls. Then lower balls are nearer to each other than upper balls, as measured with their local meter stick.

At the same time blue balls shrink vertically (along a radius to the Earth center) and so does the vertical meter stick in the ball. Therefore their relative vertical distance, as measured with this local meter stick, enlarges. The nearer to the Earth surface, the faster the ball vertically shrinks.

Let's call the meter stick embodied by the diameter of a ball the atomic meter stick. And the second measured by the clock in the ball an atomic second. This refers to the fact that all kind of clocks consist of at least one elementary particle (like the photon), or assemblages of particles like atoms.

In C of Fig. 1, when the most upper balls have 1 meter mutual distance, until the expanding surface of the Earth would hit them, they will stay at 1 meter mutual distance, since the balls were at rest and stay at rest, in coordinate system C. We call this meter the free falling meter. The coordinate system is polar, so lower balls have a little smaller mutual distance, but also this distance, like all distances, will remain constant. (But how to define the free falling second then?)

Suppose you had a probing rocket, that at nearly light speed swiftly could travel between the balls, and the center of the Earth. When probing horizontally (balls of same height above the Earth surface) the horizontal atomic meter stick in the rocket doesn't change. (The atomic meter doesn't change along horizontal tracks that take no time. The rocket's probing track takes some time and in that time the meter stick elongates a tiny little bit, but we ignore that.)

When probing vertically the horizontal atomic rocket meter stick elongates severely and the vertical rocket meter stick does shrink a lot. When lowering height to half the distance to the center of the Earth the horizontal rocket meter stick has halved. When returning to original location this changes becomes undone again. This is because GR says there is no difference between gravitation and an acceleration of corresponding size.

Here it is the acceleration that makes the meter stick to shrink or elongate. At the way from an upper ball to a lower one the acceleration makes the meter stick to shrink, while in the other way around to the upper ball the meter stick would elongate to its original size. This then must count as a negative acceleration. This is not just the acceleration in opposite direction. Precisely as there is a metric for space and time there must be an acceleration tensor. Acceleration is not a value nor a vector, acceleration is a tensor. And somehow the acceleration tensor is inverted.

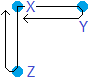          Fig. 2

Now focus on 3 balls in A, the start state of Fig. 1, see Fig. 2 Suppose the center of ball X has equal distance to the centers of Y and Z. Two photons are emitted simultaneous from the center of ball X to the centers of ball Y and Z. There the photons reflect and return to ball X. In start state 1 of Fig. 1 the photons will be back simultaneous. (We assume in the short time the photons need for their journey, the start state doesn't evolve significantly.) In end state 2 they will not be back simultaneous: photon Y (the photon from X to Y and back again) will arrive earlier than photon Z, since X and Y had approached each other, while X and Z had receded from each other. Events that are simultaneous and at same location in the system of rods and clocks will be simultaneous and at same location in the system of free falling clocks. So also in C, the system of free falling clocks, the two photons will not arrive back again simultaneous in ball X.

But in the system of free falling clocks nothing moves. The balls in A were standing still and remain standing still and so they do in C. By standing still we mean: the mass centers of the balls and the Earth don't move. All ball's surfaces distort and the Earth surface approaches because the Earth expands. So there is displacement of surfaces.

But we don't deal with surfaces, the photons traveled from center to center and those centers didn't move. There is only one solution: in the free falling system the speed of light no longer is a constant! In the system of rods and clocks it is. Measured with atomic meter sticks and atomic seconds - that's all we have in our measurement instruments! - c always remains c. But measured with free falling meters and free falling seconds the horizontal speed of light increases, while the vertical speed of light slows down.

Is this the so-called tilt of light cones, when shifting from one place in the gravitational field to a place of quite different gravitation?