End of Chapter 1
Conclusions 
1.1) Space and time are quantized and are made of particles (so-called vacuum particles).
1.2) The gravitation law of Newton is derived in a way that fits in with a kind of Higgs field absorption AND that fits in with the premises of GR.
1.3) GR is valid. Only some details differ. Light doesn’t gravitate. Wavefunctions always start out in flat space. Renormalization procedure takes place in flat space.
1.4) The Einstein equation is G = 8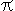
γT, where γ is the gravitational constant. The equation you work with is G * T
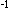= 8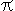γ * [1], where [1] is the 4*4 unitary matrix, describing curvature zero. This is of course the same equation as Einstein’s, but the interpretation differs.
1.5) The action of absorbing mass from the Higgs field curves spacetime. The action of gravity restores zero curvature. The background vacuum grid remains flat Minkowski space.
Discussion
1.1) We can understand how the normal filled vacuum preserves its volume: the vacuum marbles maintain touching positions. But the empty shell does not consist of vacuum marbles. There is no space behind the space to measure distances when the vacuum marble sea is absent. So how does the empty shell preserves its volume?
1.2) The identification of the jerkily sequence of displacements with a smooth velocity of a Higgs field, is this identification justified? I had a previous attempt with the jerkily displacements in one wavefunction A and the smooth velocity of a Higgs field in another wavefunction B and those two wavefunctions then should be indistinguishable. When it comes to observation A or B would be made real, depending on coincedence. When A turned out to be observed then a displacement remains but no increase of velocity. When B is observed then the displacement as well as the velocity increase remains. Leading to a kind of average velocity increase, an average acceleration.
1.3) In how far can well known fluid equations in flat space give shape to the streaming
of vacuum particles?
1.4) What if - just a thought experiment! - there is GR but no SR? Only Newtonian gravitation? When a light ray passes by the Earth and is deflected by the Earth gravitational field, then the deflection according to GR is twice the deflection according to Newton. Consider what is left when you remove SR from GR by lightspeed approaching infinity. As far as I understand a kind of empty theory remains. That is, you only get the Newtonian gravitation in matrix form (tensor form). All extraordinary effects like the slowing down of time in strong gravitational fields will have disappeared, isn't it? So, when restoring lightspeed = c, I expect SR in Newtonian gravitation also will double the angle of deflection.
1.5) at the end of State 3 at previous page is stated that renormalization procedure is set up as new every time a coupling is made. This is taken as to conclude renormalization performs in flat space. In paragraph Renormalization at page 4 of THE COLLAPSE OF THE WAVEFUNCTION are given two arguments, ARGUMENT 1 concludes this indeed is right, ARGUMENT 2 concludes this is wrong, and subsequently is concluded that decision between these two arguments cannot be made yet. Is that true?
