THE SURFACE OF THE SPHERE

Geometry as it is meant to be

The circumference of the circle

Imagine a picture completely assembled from small line segments, little pieces of straight lines, like the hair of the person in the picture. When you enlarge the picture as in a copier, every segment will be magnified with the same factor. All enlarged segments have the same ratio relative to each other as before.

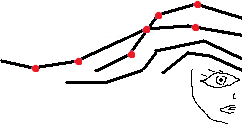
Imagine another picture assembled from straight and curved segments. Tailors and seamstresses use tape measures. Lay such a tape measure along every segment and make a photograph of the picture. When the photograph is magnified in the copier, the number of scale indents along every segment has remained the same.

Approach each curved segment by laying a chain of n small straight segments along the curve, n = an integer. The picture now consists of straight segments only. For n approaching to infinity the chain approaches the curve. When you enlarge the picture in the copier every segment will be magnified with the same factor, no matter how large n grows. All enlarged segments have the same ratio relative to each other as before.

When you enlarge a picture in a copier, the length of every curve is magnified by the same factor. All segment lengths, curved as well as straight, maintain their original ratios relative to each other. They maintain their shape.

The circumference of a circle is a curve.

The diameter of a circle is a segment.

When you enlarge or reduce a circle, the ratio of the circumference and the diameter remains the same.

Measurements reveal this ratio is 3.1415...

3.1415... is called

Circumference / diameter =

When r = the radius of the circle then the diameter of the circle = 2 r.

Circumference of the circle = 2 r

This result is not derived, in fact. It is a theorem, an observation.

There are a lot of formulas to calculate .