1. IONS PUSHED TO ONE SIDE OF THE STALK
3. BOL'S IN VERTICAL MOTION - THE LORENTZ FORCE
4. BOL'S IN VERTICAL MOTION - PART 2
5. THE SUPERBOL AND ALTERNATING CURRENTS
13. MAGNETIC DUST SUCKED IN AND SPRAYED OUT
I wished I had done better at school, when I was young. I wished I had finished university. Then I should have been better on calculation. I could have calculated the magnitude of all the mentioned effects and estimate their outcome in numbers.
Above the crop floats a BoL. For the moment it hangs there perfectly still. No force from the BoL's circlecurrent acts on the electric charges of the ions in the stalks. As long as the circlecurrent doesn't change, its accompanying magnetic field doesn't change either. A magnetic field that doesn't change and doesn't move exerts no force on electrical charges that are standing still, like the ions in the stalk (Lorentz force law). So for the moment nothing happens.
Suddenly the BoL moves upward. For practical reasons we do not take the BoL starting its movement in the air, above the crop, but in stead from the soil's surface. That is, we take the circlecurrent lying flat on the soil, half of the BoL is below soil surface. To understand what happens now we everywhere decompose the magnetic field of the BoL in one component in the horizontal plane and a second component along the vertical line. In the right part of fig. 3.1 is shown the magnetic field in point A (fat blue arrow). You have to imagine this decomposition in all points of the magnetic field. In this case the vertical component lies along the BoL's velocity direction. When the velocity of an electric charge is along the magnetic field line through the electric charge, the magnetic field exerts no force on the charge (Lorentz force law). The magnetic component in the horizontal plane is the only force working here.
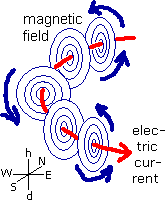
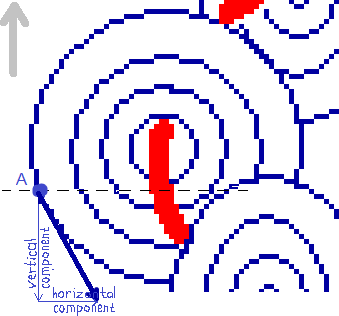
Fig. 3.1
Accepted rules in EM state that the current (red arrow) and the direction of rotation of the magnetic field (blue arrows) fit to each other as the direction in which a right hand screw would move when you turn it. When you drive a right hand screw in the wood - clockwise rotation - the screw goes forward, into the wood. When you turn the same screw counterclockwise the screw moves the other direction, out of the wood: both directions have reversed, maintaining orientation relative to each other.
We are now going to look what happens in one specific plane. We take for analysis a horizontal plane just a small distance below the circlecurrent (the black dashed line). In the four large circles of fig. 3.2 the BoL (and with it our plane of analysis) is viewed from above and if the BoL moves you move along with the BoL's velocity. Again we start when the circlecurrent lies on the soil and half of the BoL is beneath soil surface. Then the BoL gaines an upward velocity and immediately starts to rise. However, since you move along with the BoL, in your frame of reference you see the BoL standing still and the soil of the earth receding below the BoL. Since velocity is relative, you are free to choose this point of view as your standing-still base. For reasons of simplicity, we assume the ions in the stalks of the crop to have a positive electric charge. If they had a negative charge all forces (light blue arrows) would point in the opposite direction.
red = electric currents and electric charges
green = crop
light blue = force
E = electric
deep blue = magnets and magnetic field
brown = soil
grey = velocity
M = magnetic
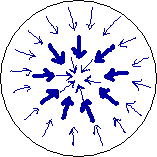
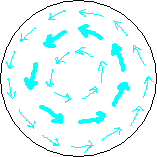
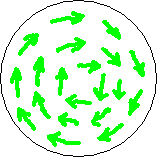
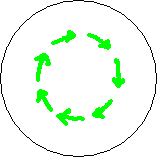
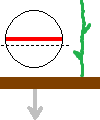
 Fig. 3.2
Fig. 3.2
The inward bound dark blue arrows in the first circle depict the magnetic field of the BoL (horizontal component only) in our plane of analysis during its fligt from the soil to let's say 2 inches above the crop. The ring of fat arrows means the field is stronger there (the circle just below the circlecurrent), thin arrows give weaker field. In the period of time we are considering, the magnetic field doesn't change. Since we have chosen our plane of analysis to move along with the BoL, the magnetic field in our plane of analysis doesn't change either.
The swirling light blue arrows of the second circle depict the forcefield in our plane of analysis. It is the force exerted by the BoL's magnetic field on the moving charges (the ions) in the crop during the time our plane of analysis crosses the crop. The ring of fat light blue arrows (strong force there) lays on the same place as the ring of fat dark blue arrows (strong field). Mind, magnetic field is not the same as force. A magnetic field at the location of an electric charge always gives a force on that electric charge that is perpendicular to the direction of the magnetic field there (AND perpendicular to the velocity. No velocity, no force.)
Green arrows in the third circle point in the lay-direction of the crop. As depicted in fig. 1.1 (opens popup), when the force on the ions is in one direction the lay of the crop is in the opposite direction. If the weaker part of the field cannot reach the necessary ion concentration in the stalks, only a ring appears, at the location of the fat arrows (fourth circle). Since we have chosen our plane of analysis to stand still with respect to the BoL, the crop in the shown third and fourth circle is moving downward through our plane of analysis.
The small picture depicts the BoL's circlecurrent (red) as viewed from aside and its current plane of analysis (black dashed line) at the moment it has risen from the soil a few decimetres. It also shows the velocity (grey) of the ground (brown) with respect to the BoL, which in fact is the velocity of the stalk's ions in the magnetic field of the BoL.
If the BoL had started above the crop and moved downward towards the crop (instead of upward) and went through the crop until its circlecurrent hits the ground and disappears, Lorentz law then gives the picture of fig. 3.3. The magnetic field remained the same but the forcefield has reversed direction, and so the lay of the crop.
red = electric currents and electric charges
green = crop
light blue = force
E = electric
deep blue = magnets and magnetic field
brown = soil
grey = velocity
M = magnetic


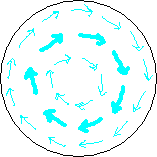
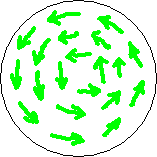
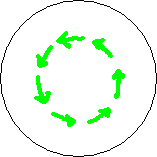
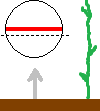
 Fig. 3.3
Fig. 3.3
On this page so far I had in mind the magnetic field of the BoL causing an ion concentration to one side of the stalk and then the asymmetric grow-pulse as means of downing. What about the downing-by-radiation version, the downing by steam-expansion at one side of the stalk? It works more or less the same; by means of growth or by means of steam-expansion, both ways have asymmetric enlarging of the stalk at the location of the ion concentration (however not necessarily the same ions). What worries is the threshold: there is no reason why below a certain threshold an ion suddenly would absorb no radiation no more. Therefore there isn't a well-defined threshold. But look at the fields.
The strength of the magnetic field causing the ion concentration, drops with the distance, causing lesser ions concentrated when further away from the BoL. Radiation intensity, when one single BoL is the source, drops with the distance too, causing lesser radiation absorbed by any ion when further away from the BoL. As an effect the over-all heating may drop that quickly at a certain distance that it sufficiently serves as a threshold. A threshold is needed to get those beautiful sharp edges seen at most cropcircles.
If not sufficient one expects instead a transition area at the border of half-downed crop. Which indeed now and then is observed.
Only calculation or simulation can tell. Or maybe experiment. Page 7 is about experiments.
Shall we now celebrate We have a cropcircle! We made a cropcircle!
Well, except from experiment to show it actually works, there is a small set-back effect. Follow me to the next page!