Quaternions 
Quaternions
by Vincent van der Noort
Utrecht University
In my lecture I gave a number of arguments for the (implicit) statement in this title, but for the most beautiful aspect of the four-dimensional space, namely that you can interpret the points in that space as numbers, the quaternions, little time remained. That is why I will go into that in more detail in this text, instead of recounting the examples from my lecture.
The text below also appeared in slightly different form in the book Getallen zijn je beste vrienden (Numbers are your best friends), published by Atheneum - Polak and van Gennep, 2011, by Vincent van der Noort, which also contains more information about the other examples from the lecture.
You should know the complex numbers. On the one hand, complex numbers are the end point of a long development in which people have shamelessly invented more and more new types of numbers (non-integers, negative numbers, etc.). If you only know natural numbers, it is easy to come up with a question to which the answer is an as yet unknown number such as 'To which number do you have to add 3 to get 2?' Or 'Which number do you have to multiply by itself to get 3?'. Once you have the complex numbers at your disposal, you can stop inventing new numbers: all the answers to these kinds of questions are complex numbers themselves. The complex numbers are happy with each other and don't need anyone else, a result known as the Algebra Principle.
On the other hand, complex numbers also shed new light on an area that apparently has little to do with numbers: flat (two-dimensional) geometry. By seeing the points of the plane as numbers, all kinds of geometrically interesting operations (rotations, reflections, elongations, shifts and more complicated deformations that can be composed of them) are suddenly very easy to describe in terms of addition, subtraction, multiplication and division. Actually, we already have something similar with the real numbers, which you can see as points on the (one-dimensional) line. Shifting a piece of line by a distance of 3 means adding 3 to all numbers in the piece of line. Mirroring a piece of number line in 0 is multiplying all numbers in that piece of line by -1. However, we don't live in a one- or two-dimensional world but in a three-dimensional one. And geometry in three dimensions, especially when we start to rotate, mirror and distort, is a lot more difficult to see than geometry in two dimensions. Given the success of the complex plane, it would be extremely useful if more numbers existed outside the complex numbers we already know, numbers that are so many that they fill up a whole three-dimensional space. Ideally, complex rotations and distortions in space would then be described as adding and multiplying these numbers. In short, there is indeed a market for more numbers than the complex, but the motivation now comes not from their properties as numbers, but from geometry.
This brilliant thought is not my own, but from the Irish mathematician William Rowan Hamilton (1805-1865). As mentioned, the use of pictures in mathematical evidence in the nineteenth century aroused suspicion. The geometric properties of complex numbers were used to better understand their properties as numbers, but it remained an aid. Hamilton, however, turned his head one hundred and eighty degrees and considered the number properties as a useful tool for doing geometry. So handy, in fact, that he was convinced there should be more numbers to simplify understanding geometry in three dimensions. New numbers, not because the numbers call for it, but the geometry does so - a revolutionary idea.
Hamilton was therefore not the least. He was one of those rare geniuses who speak more languages at some point in their lives than they are years old (in his case at thirteen) and also wrote poems in all those languages (although his friend Wordsworth didn't think his work was poetry). At eighteen, without ever going to school (he was previously taught by his uncle), he was admitted to Cambridge University, where he consistently won all the awards for best student. However, not everything he touched turned to gold. Shortly after arriving in Cambridge, he fell in love with Catherine Disney, the daughter of a friend of his uncle. It was clear from the start that it could not work: her father was against marriage because he believed that such a student would never have a prospect of a steady job with a decent salary. This was a little premature: at the age of twenty-two (!) Hamilton became professor of astronomy. However, it was already too late then. In the spring after her meeting with Hamilton, Catherine married a priest 15 years older than her, who in the eyes of the Disney family could provide her with more security. For a year, William was consumed with grief, which translated, among other things, into that he no longer just got A's (tens) for his exams, but A-minuses.
After graduation, Hamilton fared better, making one brilliant discovery in physics after another and marrying Helen Maria Bayly, a neighbor of the observatory where he had lived since being appointed Royal Astronomer of Ireland. Together they had three children.
However, Hamilton had not lost his tendency towards great compelling unhappy loves, and now that he had a wife and children he found them in the form of the aforementioned idea that there must be numbers that are so many, even more than the complex numbers, that they occupy all points of a three-dimensional space. A spectacular idea as said, but there is still a long way between having a good idea and making a revolutionary invention. Hamilton spent sixteen years of his life looking for these numbers without any success. This did not lessen his obsession. Every morning at breakfast his children asked, 'And father, can you multiply triplets already?' (Just like modern mathematicians Hamilton thought about a point in three dimensional space as a row of three numbers - nowadays we should say coordinates.) And every morning he had to disappoint them, or rather himself. You can imagine what an agony this must have been for the Hamilton family.
In modern eyes, Hamilton's agony seems a bit strange: the new numbers he was looking for didn't yet exist, in fact, no one had ever thought about it, so he was in the perfect position to invent them himself. Like the mythical inventor of the game of chess, he could have simply drawn up the rules according to which the points in space should be multiplied together and could have given these new numbers a nice name. An easy example is the multiplication ★ you get by multiplying 'coordinate wise': (2, 3, 4) ★ (5, 6, 7) = (2 * 5, 3 * 6, 4 * 7) = (10, 18, 28). Another more geometric example is the multiplication ◇ where you draw a line between the two numbers you want to multiply and draw the product on the same line, exactly between the two points.
At first glance, one can invent a thousand multiplication rules like this, and probably Hamilton did. But apparently he all felt that the resulting 'multiplication' was a fun thought game, but not a real multiplication of true numbers. We can only guess what exactly he set for the demands on a number. However, we can come up with arguments ourselves why the multiplications like ◇ are no good (and no one ever uses them): if we multiply points on space with multiplication ◇ there is no point that can play the role of the number 1 in the sense that 1 ◇ x = x for all numbers x. Extending the number line to more dimensions is nice, but if that means sacrificing the number 1, you throw the baby away with the bath water.
The multiplication ★ does not have this problem but there is the problem that you cannot divide: (2, 2, 4) ★ (5, 0, 0) = (10, 0, 0) but (2, 12, 6) ★ (5, 0, 0) is also equal to (10, 0, 0). What then is (10, 0, 0) divided by (5, 0, 0)? (2, 2, 4) or (2, 12, 6)? We will never know. Nowadays it is known that whatever crazy multiplication you impose on the points of a three-dimensional space, you will never be able to divide. But Hamilton (at least at the beginning of his search) was unaware of this. He didn't think in terms of 'crazy multiplications' at all, he was just looking for the only correct extension of the complex number plane to three dimensions.
This chapter is likely to become a tragedy of the type 'brilliant mathematician wastes his life on insoluble problem' (for example, read the novel Uncle Petros and conjecture of Golbach by Apostolis Doxiadis) but this will not be so. In this case, after sixteen years of frustration and nagging children, there is an unexpected happy ending. Place of action is the Royal Canal in Dublin where Hamilton takes a walk with his wife. I now quote Hamilton himself: 'And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples (...) An electric circuit seemed to close, and a spark flashed forth.' Delirious with joy, Hamilton takes his pocket knife and carves his magical formula
i
= j = k = ijk = -1
in the nearest bridge: the Brougham Bridge. Incidentally, the inscription has never been found, but Irish mathematicians still walk every year to this place to honor Hamilton and gain inspiration. For convenience, the Irish Mathematical Society has affixed only a plaque with the above text on the bridge.
What was Hamilton's liberating insight? At the decisive moment, he realized that his attempts to expand numbers to three dimensions were futile, but if he went a step further and expanded the number line to four dimensions, everything would suddenly fit together perfectly. In addition to the regular real numbers and the root i of -1, Hamiton introduced another two roots of -1 which he called j and k. Hence his formula i = j = k = -1. All numbers you can make with 1, i, j and k fill up a four-dimensional space and he called them quaternions. A random quaternion consists of a number of times 1 plus a number of times i plus a number of times j plus a number of times k, so we can write it as a + bi + cj + dk with a, b, c and d familiar real numbers . One of my favorite quaternions is 1/2 + 1/2 i + 1/2 j + 1/2 k; we will return to this later.
The idea of giving -1 extra square roots seems a bit strange at first glance. In the complex numbers -1 has only two roots: i and -i. That is not a special property of -1: every complex number except zero has exactly two roots (for example, 4 has roots 2 and -2) and they have to do with that. It is not without reason. For example, if we write out the multiplication (i + j) * (i - j) we get i * i + j * i - i * j - j * j = -1 + ji - ij - (- 1) = ji - ij. This seems to be equal to 0 and we don't want that. After all, 0 * (i - j) is also equal to 0 and so we do not know what 0 divided by i -j is: i + j or 0? Hamilton solved this problem in a particularly elegant way. ji - ij is not equal to zero, he said, because ij is not equal to ji! To be precise: i times j equals k, but j times i equals -k. Likewise, jk = i but kj = -i and finally ki = j but ik = -j. This is what his last equation ijk = -1 expresses.
Returning to the example, (i + j) (i - j) is not equal to 0 but to -2k. The idea that x times y does not have to be the same as y times x was completely new and groundbreaking. We are so used to 4 times 3 being the same thing as 3 times 4 that we don't think about it anymore. But it is exactly what it takes to make quaternion multiplication work. Incidentally, within quaternions 4 * 3 is still the same as 3 * 4, just as 4 * j is the same as j * 4, usually called 4j.
Hamilton decided to devote the rest of his life to studying quaternions. Given his great talent for mathematics and physics, it may be a pity, but personally I can understand it. Quaternions are my great math childhood sweetheart. Calculating with quaternions is fun - it's like learning to calculate again and everything is new and exciting. Because x times y is not always the same as y times x you have to keep your attention a little better and because all numbers consist of four parts, it is difficult to predict in advance what the result of a calculation will be. As a result you sometimes discover beautiful new and unexpected structures. Moreover, the image of quaternions as points in a four-dimensional space gives you the feeling that you can really imagine something in the calculations.
Just as the two-dimensional world of complex numbers is described by two axes: a real axis and an imaginary axis, so we have four axes in the four-dimensional space of the quaternions: one from O through 1 (on which the ordinary real numbers lie) , one through O and i, one through O and j and one through O and k. If we recall the description of the four-dimensional platonic bodies in the lectures, we see that the eight points that are at a distance 1 from the origin on these axes: 1, -1, i, -i, j, -j, k, -k together form the vertices of a four-dimensional octahedron. If we see the vertices of this octahedron as numbers that we can multiply, we discover something nice: as long as we stick to multiplication and do not add up, we don't need anything outside of these eight numbers. The product of two of the vertices of the fourth-dimensional octahedron is another one of those eight vertices. Together they live in their own happy world where the rest of the quaternions have no business. You may wonder if the vertices of the four-dimensional cube also have this property. Of course there are a lot of places in the four-dimensional space where you can place a four-dimensional cube, but here we choose the cube with vertices ±1/2 ± 1/2 i ± 1/2 j ± 1/2 k. Everywhere there is a ± , you can fill in a + or a - sign, so in total this gives sixteen different combinations: the sixteen vertices of a four-dimensional cube. The advantage of this choice is that the cube has center point 0 and ribs of length 1 that run parallel to the axes.
The question was whether something special happens when we multiply the points of the cube with each other and at first sight the answer seems no. If we find the previously mentioned number 1/2 + 1/2 i + 1/2 j + 1/2 k multiplying by itself, we find (calculate please) the answer -1/2 + 1/2i + 1/2j + 1/2 k what one step further is in the cube. But if we multiply this again by 1/2 + 1/2 i + 1/2 j + 1/2 k, we suddenly end up at -1! In itself very special, but this number is no longer in the cube. However, we add the sixteen points of the four-dimensional cube together with the eight points of the four-dimensional octahedron above, it turns out that the twenty-four quaternions that we get together form a closed world: whichever two of these numbers you choose, the product is always one of those twenty-four. Moreover, it appears that these twenty-four numbers together form the vertices of the smallest exceptional platonic body: the twenty-four cell.
All this four-dimensional geometry is nice, but what Hamilton was all about was understanding three-dimensional geometry. After all, we live in a three-dimensional world. Here, too, the quaternions hold their own. Hamilton introduced the so-called pure quaternions, quaternions of the form bi + cj + dk that you get when you ignore all real numbers. These form a three-dimensional space (within the four-dimensional space of all quaternions you can see the pure quaternions as the three-dimensional 'plane' that is perpendicular to the line of real numbers) and it was this space in which Hamilton did his geometry.
All 'rigid' movements in three-dimensional space are a combination of rotations, reflections and shifts and all three can be easily described with quaternions. Shifts are easiest. Shifting the three-dimensional world is simply adding a fixed pure quaternion to each point. Then reflections. The spherical shell of pure quaternions at a distance 1 from the origin plays a special role. Every point u on this sphere defines a plane: we draw the line through 0 and u and look at the plane through 0 in the three-dimensional space that is perpendicular to it. If we want to know what mirroring is in this plane, we have enough by u. If we look at an arbitrary pure quaternion x, the point we find by mirroring x in the plane described by u is equal to the result of the multiplication uxu. It is not shorter to write this as ux because ux and xu don't have to be the same. However, the symmetrical notation uxu of course fits much better with the phenomenon of mirroring, so we cannot be very sorry about this.
So with quaternions we can calculate very quickly and easily how you mirror a point (or a collection of points) in an arbitrary plane through the origin. Because we also understand how shifts work, mirroring in any plane in space has become a piece of cake. Best of all, however, are rotations. For this, it is necessary to understand how division in the quaternions works.
As I described above, I suspect that Hamilton would not accept multiplication as multiplication until it also allows some form of division. This is indeed the case with quaternion multiplication. However, we should be a little careful: the fact that xy is not always the same as yx also casts its shadows on the world of division. Let's start with the good news: for any quaternion q (except 0) we can calculate the quaternion 1/q without any doubt or ambiguity. Usually this quaternion is not noted as 1/q but as q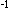
, the 'inverse' of q. If q = a + bi + cj + dk (herein a, b, c, d are real numbers) then q 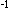= (a -bi -cj -dk) / (a + b + c + d). You can check for yourself that q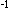q = q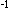q = 1. With a little more effort, it can also be seen that q 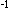is the only quaternion that has this property and therefore deserves the name '1 divided by q'.
Since dividing by q is the same as multiplying by its inverse (10 divided by 2 is the same as 10 times 1/2; 9 divided by 3 is the same as 1/3 times 9) we also know how to divide a random quaterion r by a quaternion q: dividing by q is simply multiplying by q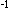. Since r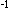q and q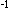r don't have to be the same, we have to distinguish between 'dividing r from left by q' and 'dividing r from right by q', but as long as we keep saying neatly what kind of dividing we use, everything works perfect.
An example. The inverse i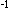 of i is -i, because (-i) i = - (- 1) = 1. This gives two different forms of 'k divided by i': k from the left divided by i is i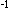k = (-i) k = j and k from the right divided by i = k i 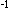= k (-i) = -ki = -j. Note that both interpretations of 'k divided by i' are in line with our idea of how division should relate to multiplication: k / i = j 'because' ij = k and k / i = -j 'because' (-j) i = k.
Back to rotations. If we multiply a pure quaternion x from the left by a non-zero quaternion q and then divide it again from the left by q, the answer is of course equal to x again. Now if we multiply x again from the left by q but this time divide it from the right by q, then the result qxq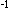 does not necessarily have to be equal to x, but our sense of justice says that it cannot differ too much from x either. That feeling is correct, qxq 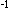is again a pure quaternion and has the same distance to 0 as x. This means that the transition from x to qxq 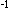can be described geometrically (in several ways) as a rotation through a certain angle about a certain axis through the origin. And now comes the miracle: one of those rotations has the magical property that if we take another arbitrary pure quaternion y, the transition from y to qyq 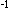can be described as a rotation about the same axis and the same angle. So that axis and angle depend only on q - the quaternion q, in short, defines a rotation about the origin in three-dimensional space. Each quaternion defines a rotation, and conversely, each rotation is described by a quaternion. By an infinite number of quaternions in fact, because q and 2q and -q and aq for every other real number a all define the same rotation. A rotation about the axis through i at an angle of ninety degrees is described, for example, by the quaternion 1 + i. If we let this work on j then we expect to end up in k and indeed: (1 + i) j (1 + i) 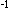= (1 + i) j (1/2 -1/2i) = 1j1/2 + 1y (-1/2i) + ij1/2 + ij (-1/2i) = 1/2j + 1/2k + 1/2k - 1/2j = k. If we let this work on i + j + k, we expect to end up in i - j + k and you can calculate for yourself that this is also correct.
An immediate consequence of the description of rotations as quaternion multiplication is that if I first rotate the world according to quaternion q and then according to quaternion r (so possibly around a completely different axis and angle) I could also have obtained the same result by only rotating once (about yet another axis): the rotation associated with the quaternion rq.
Although that fact (the seemingly inimitable displacement of points in space that you get by performing two rotations in succession is the net result of one simple rotation) may have been known before Hamilton, I still find it a surprising result.
As mentioned, Hamilton devoted the rest of his life to quaternions, which resulted in several thick books. Fortunately for him, the quaternions did not miss their impact. Physicists loved the quick way of describing rotations and other movements in space, and mathematicians saw their eyes opened by this new geometric way of thinking about numbers and plunged massively into the search for numbers in eight and sixteen dimensions.
However, this search only lasted a few years because the outcome turned out to be somewhat disappointing. Every time you double the dimensions you pay a price. In the transition from real to complex, you lose the notion of larger and smaller. At the transition to quaternions you lose the rule xy = yx. You can still live with that. In the next step, to the octonions in eight dimensions, you lose a property of numbers that is so obvious that no one ever thought about it before the discovery of octonions in 1843, namely that (xy) z = x (yz). (So, if we take x = 3, y = 4, z = 5, that 12 * 5 = 3 * 20 which is indeed true.) The absence of this property means that almost no one is interested to calculate at octonions and they are considered a complete curiosity rather than numbers.
Back to quaternions now. The United States even declared that quaternions were the (only) math that all students at their universities had to learn. At the end of the nineteenth century, the quaternions went down because of their own success. One of those Americans, the physicist Gibbs, noted that as a physicist he in practice only multiplied pure, three-dimensional quaternions and never the full quaternions of four terms. Not surprising, of course, because we live in a three-dimensional world and not in a four-dimensional one. The result of such a multiplication usually is a quaternion with four terms, say a + bi + cj + dk. However, Gibbs, with his critical eye, found that in some calculations he and his colleagues needed only the real part (a) of this result and in others only the quaternion part (bi + cj + dk) but never the quaternion as a whole.
The real part of a quaternion is a number, something we've known and loved all our lives. The quaternion part is a point in space, something we are equally familiar with. The quaternion as a whole, on the other hand, lives in an invisible four-dimensional space, making it a terrifyingly abstract concept that most of Gibbs' students had a lot of trouble with. Wouldn't it be much easier, he reasoned, if you can, from two points in space u an v, immediately calculate the real part and the quaternion part of uv without ever needing the product uv (or the whole idea that points in space are also numbers)? No sooner said than done. Gibbs introduced the notation u * v for the real part of uv and the notation u X v for the quaternion part and described his new operations * (the 'inner product') and X (the 'outer product') in such a way that the things you multiplied were not numbers, but simply points in space.
Gibb's new notations were a resounding success. After all, people want to do their calculations efficiently and, apart from a few dazed romantic like me, are not interested in the magical number world that lies behind it. Still the inner and outer product are among the first things you learn when you start studying mathematics or physics and the quaternions seem to have been completely forgotten. In the late twentieth century, however, the quaternions struck back merciless. As mentioned, every quaternion describes a rotation. In many physical applications where something rotates you do not need to calculate that rotation, you want to know at most about which axis the rotation takes place and what the speed is. However, things are different in the world of computer graphics and virtual reality. A flight simulator that wants to give the driver the idea to turn over in a weird direction has to calculate in a fraction of a second of every point in the (virtual) space where it is being rotated to. That's exactly what quaternions are good at: multiply each point from the left by q and from the right by q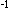, where q is the quaternion that describes the desired rotation, and there you are. A more obvious way to describe rotations is to say from three standard reference points in space (say (1, 0, 0), (0, 1, 0) and (0, 0, 1)) where they are to be rotated to. The end position of the other points is then easy to calculate. To describe a random rotation you need nine numbers: three for the new spot of (1, 0, 0), three for the new spot of (0, 1, 0) and three for the new spot of (0 , 0, 1). With a quaternion you only need four numbers.
This does not seem like such a big difference, but who wants to multiply many quaternions to find complex compositions of rotations is done a lot faster than who multiplies as many blocks of three by three numbers (matrices).
And in the world of computers, everything has to be fast, faster, fastest - a pilot in training doesn't want to drop the effects of his action plop plop plop at one frame per second when he pulls on the control stick.
It goes a long way to say that quaternions save lives, but if you're playing a computer game tomorrow and you notice how fluid and credible all three-dimensional movements look, think again about Hamilton and what misery he endured to make this possible.