then it has to be of intensity I
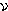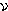^3 ( = frequency).The Lorentz invariant
zero-point radiation field
Quotes from
T.H. BOYER, THE CLASSICAL VACUUM
Scientific American august 1985
If there is a Lorentz invariant field of all possible frequencies,
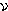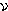then it has to be of intensity I ^3 ( = frequency).
The piston is at the closed end of the cylinder and there is no vacant space at all. Then the piston is withdrawn, leaving a vacuum behind. The walls of the cylinder were emitting heat radiation into the vacuum region. When the piston was forced back in, this radiation was compressed. Thermal radiation responds to compression much as a gas does: both the pressure and the temperature rise. (...)
Wien assumed perfect isolation of the piston and the cylinder so that no heat could be gained or lost. The intensity of heat radiation turned out to be proportional to the cube of the frequency, I 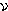^3, and proportional to T / 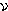, T is the temperature in K. (...)
An electron in steady oscillation radiates electromagnetic waves at the frequency of oscillation. (...)
Roughly speaking, the 19th-century version of classical electron theory assumed that at some time in the distant past the universe contained matter (electrons) but no radiation. All electromagnetic radiation evolved from the acceleration of electric charges. (...)
Between the Casimir's plates the force of the thermal radiation is proportional to the temperature divided by the cube of the distance between the plates, F T / d^4. This force disappears at absolute zero as the thermal radiation itself does. (...)
Casimir's plates are two electrically conducting parallel plates about 10^-6 m apart. Because the plates are conducting, they reflect electromagnetic waves; for a wave to be reflected there must be a node of the electric field - a point of zero electric amplitude - at the surface of the plate.
The Casimir force by which the plates are attracted / pushed together, is proportional to the area of the plates A divided by the fourth power of their separation d,
F(cas) = 1.3 * 10^-18 erg cm * A / d^4.
1 erg cm = 10^-7 J * 10^-2 m = 10^-9 Jm,
so 1.3 * 10^-18 erg cm = 1.3 10^-9 Jm.
The constant is in 1058 found by M. J. Sparnaay. For A = 1 cm^2 and d = 0.5 * 10^-6 m is F = the weight of 0.2 milligram. (...)
It turns out that the zero-point spectrum can have only one possible shape if the radiation is to be Lorentz invariant. The intensity of the radiation at any frequency must be proportional to the cube of that frequency, I 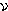^3. A spectrum defined by such a cube curve is the same for all unaccelerated observers, no matter what their velocity; moreover it is the only spectrum that has this property.
The spectrum predicts an infinite energy density for the vacuum. (...)
Under equilibrium conditions, when no external force is applied to the piston, there is radiation both inside and outside the cylinder, and the radiation pressures acting on the piston are balanced. This balance holds for both thermal and zero-point radiation. When the piston is pushed into the cylinder, the radiation is compressed. Wien's calculation indicates that the thermal radiation resists such compression; it increases in temperature and exerts a greater pressure against the piston. When the same analysis is made for the zero-point radiation, however, the result is different: the zero-point spectrum does not change at all in response to compression. Indeed, a spectrum described by a cubic curve is the only one that has this remarkable property. (...)
When one starts from I = Constant * 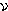^3 this gives a force between the Casimir plates of F A / d^4. Again it can be shown that the spectrum is unique in supporting this prediction; no other spectral curve yields an inverse-fourth-power dependence on distance. (...)
The Constant cannot be calculated theoretically, but Sparnaay's measurement of the force in the Casimir effect allows the value to be determined from experiment. After some preliminary algebraic manipulation it is found that the constant is equal to 3.3 * 10^-27 erg-second, a magnitude corresponding to one-half of Planck's constant, h/2. (...)
The vacuum no longer is empty of all electromagnetic fields. The version of classical electron theory with classical electromagnetic zero-point radiation, in short stochastic electrodynamics, is based on Newton's laws of motion for the electrons and Maxwell's equations for the electromagnetic field PLUS the randomly fluctuating fields having a zero-point spectrum. (...)
Imagine a harmonic oscillator made up of an electron attached to a perfectly elastic and frictionless spring. When oscillating the electron gives off electromagnetic radiation at the frequency of oscillation. On the electron act the restoring force from the spring and a reaction force arising from the emission of radiation. Because the reaction force is directed opposite to the electron's motion, the oscillations will steadily dampen and the electron will eventually come to rest. The zero-point radiation exerts a randomly fluctuating third force on the electron so that it never comes to rest. The harmonic oscillator retains an average energy of h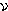/2 (...)
Consider an observer in a continuously accelerating rocket. To find out, one has to perform a Lorentz transformation from the standing still frame of reference to the accelerated one, over some time interval. It turns out the spectrum remains homogeneous and isotropic, and no change is observed as long as the rate of acceleration itself does not change. Nevertheless, the spectrum is not the one seen by an unaccelerated observer. At any given frequency the intensity of the radiation is greater in the accelerated frame than it is in the frame at rest.(...)
The equation of motion for the accelerated oscillator is much like the one valid in a fixed frame of reference. Only the radiation-reaction force has a new term proportional to the square of the acceleration, and the oscillator is exposed to a new spectrum of zero-point radiation. (...)
When an oscillator is accelerated, it jiggles more vigorously than it would if it were at rest in the vacuum. (...)
An observer in a small laboratory supported in a gravitational field makes exactly the same measurements as an observer in a small accelerating rocket (equivalence principle of Einstein). The laws of thermodynamics are found to hold in a gravitational field. So the laws of thermodynamics hold in an accelerating rocket too. There is then only one possible equilibrium spectrum that can be added to the zero-point radiation: the additional radiation must have a thermal spectrum. With any other spectrum the oscillator would not be in thermal equilibrium with its surroundings. So a physical system accelerated through the vacuum has the same equilibrium properties as an unaccelerated system immersed in thermal radiation at a temperature above absolute zero. The proper relation between acceleration and temperature was found in about 1976 by W.G. Unruh and P.C.W. Davies. An observer accelerating through the vacuum observes the zero-point radiation spectrum PLUS the spectrum of thermal radiation deduces by Plack in 1900. (...)
There is a minimum attainable temperature in a gravitational field. At the earth surface the limit is 4 * 10^-20 K. (...)
End of the Lorentz invariant zero-point radiation field