Towards the center of an electrically neutral charge distribution

Imagine the charges in our cloud to have sufficient mass to prevent quantum mechanical binding in pairs (1 pos + 1 neg -pairs). Suppose some effect had caused the cloud to be a little denser in the center than at the periphery, with a smooth transition of densities in between. Take a charge q as 1000 times lighter than the other charges of the cloud and situate q in the periphery of the cloud. A typical patch then is shown in figure 1.

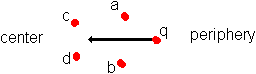Fig. 1

Is it possible you see q being accelerated to the center of the cloud? If you see this, it doesn't necessarily mean it is attracted by the center. I mean this: charge c and d are a little nearer to each other than charge a and b. Our charge q is swung from let's take velocity zero to a maximum precisely between a and b and to zero velocity again at the end of the drawn arrow. But just before the end of that arrow it had arrived in the influence of c and d. While still possessing a last bit of its velocity it starts its swung between c and d.

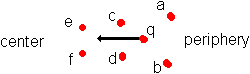Fig. 2

Just before it had reached the end of the arrow in figure 2, it had entered the next patch. There it started the next swing between e and f with just a little higher velocity than at the start of the previous swing. When this might repeat for some time, the result is a particle speeding up to the center of the cloud, suggesting it is attracted by the center. While in fact there is no action on a distance working and in stead the particle is accelerated in the subsequent patches as in a linear particle accelerator.

If the particle would deviate a little, it is not pushed back on its track but will deviate still more. The track is instable. By example:

Fig. 4

In the years 1986 and 1987 Klaas van Aarsen helped me with a particle simulation program wherein this could have been performed. It used the Runga Kutta method in its calculation kernel. I have the program on paper, I should type it in again and download a Turbo Pascal compiler.

The particle simulation program could decide this kind of things by running a cloud with one such 1000 times lighter particle q amongst them. And then repeat the experiment with all charges more than two patches away from q switched off. The difference of the two experiments should be decisive.

When q has a negative electric charge, a, b, c, d, e and f had to be positive charges. The actual situation is threedimensional and a typical distribution in a cloud of charges can be as shown in figure 3.

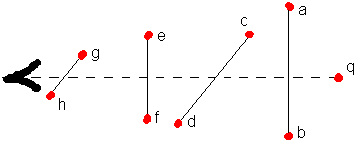Fig. 3

So far our charge q is moving in a cloud of positive electric charges only - where are the negative ones? A typical distribution in the cloud is shown in figure 5.

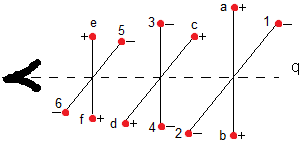Fig. 5

On the shown track the attraction F(att) by a and b on q is precisely canceled out by the repulsion F(rep) of 1 and 2. Likewise for the other charges. So in a cloud consisting of even amounts of positive and negative charges in a homogeneous distribution of space and charge, but only a little denser when nearer to the center, charge q will not be accelerated towards the center of the cloud, on the track shown. On the shown track charge q will move by with constant velocity in a constant direction - suppose it had any initial velocity.

Earlier results say an equal charge, neatly placed in the fringe of the cloud, will be dragged along with the cloud's contraction. But this is an extra charge, lighter, not neatly placed and in fact enlarging charge density at its location.

But tracks like these, precisely between charges, are rare. What will happen really when a charge like q impacts on a cloud as described?

What will happen when another cloud is speeding towards and then pervading our cloud? The two clouds will disperse each other, I expect, and finally merge when their initial relative velocity is low enough. The new cloud, with twice as much charges now, will contract like smaller clouds would do. Will it look like merging galaxies?

The MAGNETIC FIELD would make a difference, isn't it? I haven't invoked a magnetic force in my particle simulation program yet. Remember, we supplied our charges with sufficient mass to prevent them to bind in pairs, quantum mechanically. This also reduces accelerations, lowers built-up speeds and the role of the magnetic field then is diminished.

A patch doesn't know and doesn't need to know what its distance is to such things as the center of the cloud, or where the fringes are. But the contraction is not homogeneous in time, denser parts will contract faster.

The patches of space in our cloud of charges glue together when neighbouring and as soon as their relative distance becomes a little bigger their mutual attraction disappears. It looks a bit like water, the hydrogen bridges that bind H2O molecules when close enough together and break when the distance grows a little. But the patches in our cloud of charges do shrink, which is a gas-like feature. So the situation resembles more a gas of liquid, a fluidal gas.

The charge distribution in between the faster contracting parts becomes thinner and all too soon that thin that it is becoming to be interpreted as a distance between them. And since the netforce doesn't act over distances they will disconnect. Small differences in charge density will increase to larger differences. The cloud is falling apart in an innumerable amount of smaller clouds. Like primordial clouds contracting to stars?